您好,登录后才能下订单哦!
今天我们继续来学习递归,下来我们先来回顾下函数的调用过程:在程序运行后有一个特殊的内存区供函数调用使用。那么这个内存区有什么用呢?1、用于保存函数中的实参,局部变量,临时变量等;2、从起始地址开始往一个方向增长(如:高地址 --> 低地址);3、有一个专用“指针”标识当前已使用内存的“顶部”。
那么程序中的栈区,就是一段特殊的专用内存区。如下图所示
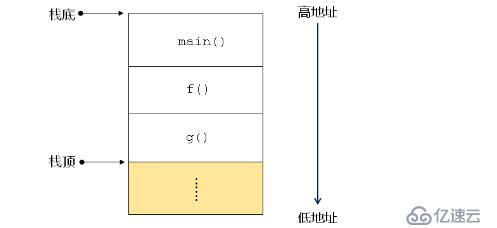
下来我们来看一个示例:逆序打印单链表中的偶数结点。如下所示
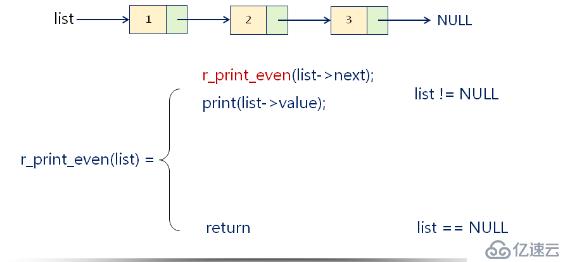
下来我们来看看具体源码是怎么实现的,如下
#include <iostream>#include <cstring>
#include "DTString.h"
#include "LinkList.h"
using namespace std;
using namespace DTLib;
struct Node
{
int value;
Node* next;
};
Node* create_list(int v, int len)
{
Node* ret = NULL;
Node* slider = NULL;
for(int i=0; i<len; i++)
{
Node* n = new Node();
n->value = v++;
n->next = NULL;
if( slider == NULL )
{
slider = n;
ret = n;
}
else
{
slider->next = n;
slider = n;
}
}
return ret;
}
void destory_list(Node* list)
{
while( list )
{
Node* del = list;
list = list->next;
delete del;
}
}
void print_list(Node* list)
{
while( list )
{
cout << list->value << "->";
list = list->next;
}
cout << "NULL" << endl;
}
void r_print_even(Node* list)
{
if( list != NULL )
{
r_print_even(list->next);
if( (list->value % 2) == 0)
{
cout << list->value << endl;
}
}
}
int main()
{
Node* list = create_list(2, 5);
print_list(list);
r_print_even(list);
return 0;
}我们来看看运行结果
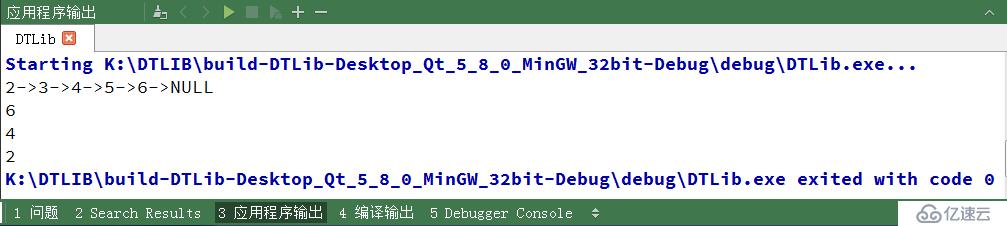
我们看到已经实现了这个功能。
下来我们来看看著名的“八皇后”问题,那么什么是八皇后问题呢?在一个 8×8 的国际棋盘上,有 8 个皇后,每个皇后占一格;要求皇后间不会出现相互“***”的现象(不能有两个皇后处于同一行、同一列或同一对角线上)。

那么实现的关键是什么呢?我们先来看看关键的数据结构定义:
1、棋盘,它便是用一个二维数组(10*10),0表示位置为空,1表示皇后,2表示边界;
2、位置,struct Pos。
struct Pos
{
int x;
int y;
}
3、方向:
水平:(-1,0),(1,0)
垂直:(0,-1),(0,1)
对角线:(-1,1),(-1,-1),(1,-1),(1,1)
其中的算法思路:
1、初始化:j = 1
2、初始化:i = 1
3、从第 j 行开始,恢复 i 的有效值(通过函数调用栈进行回溯),判断第 i 个位置
a. 位置 i 可放入皇后:标记位置(i,j),j++,转步骤 2
b. 位置 i 不可放入皇后:i++,转步骤 a
c. 当 i > 8 时,j--,转步骤 3
-- 结束:第 8 行有位置可放入皇后。
下来我们来看看具体的源码实现,如下
#include <iostream>
#include <cstring>
#include "DTString.h"
#include "LinkList.h"
using namespace std;
using namespace DTLib;
template < int SIZE >
class QueueSolution : public Object
{
protected:
enum { N = SIZE + 2 };
struct Pos : public Object
{
Pos(int px = 0, int py = 0) : x(px), y(py) { }
int x;
int y;
};
int m_chessboard[N][N];
Pos m_direction[3];
LinkList<Pos> m_solution;
int m_count;
void init()
{
m_count = 0;
for(int i=0; i<N; i+=(N-1))
{
for(int j=0; j<N; j++)
{
m_chessboard[i][j] = 2;
m_chessboard[j][i] = 2;
}
}
for(int i=1; i<=SIZE; i++)
{
for(int j=1; j<=SIZE; j++)
{
m_chessboard[i][j] = 0;
}
}
m_direction[0].x = -1;
m_direction[0].y = -1;
m_direction[1].x = 0;
m_direction[1].y = -1;
m_direction[2].x = 1;
m_direction[2].y = -1;
}
void print()
{
for(m_solution.move(0); !m_solution.end(); m_solution.next())
{
cout << "(" << m_solution.current().x << ", " << m_solution.current().y << ") ";
}
cout << endl;
for(int i=0; i<N; i++)
{
for(int j=0; j<N; j++)
{
switch (m_chessboard[i][j])
{
case 0: cout << " "; break;
case 1: cout << "#"; break;
case 2: cout << "*"; break;
}
}
cout << endl;
}
cout << endl;
}
bool check(int x, int y, int d)
{
bool flag = true;
do
{
x += m_direction[d].x;
y += m_direction[d].y;
flag = flag && (m_chessboard[x][y] == 0);
}
while( flag );
return (m_chessboard[x][y] == 2);
}
void run(int j)
{
if( j <= SIZE )
{
for(int i=1; i<=SIZE; i++)
{
if( check(i, j, 0) && check(i, j, 1) && check(i, j, 2) )
{
m_chessboard[i][j] = 1;
m_solution.insert(Pos(i, j));
run(j + 1);
m_chessboard[i][j] = 0;
m_solution.remove(m_solution.length() - 1);
}
}
}
else
{
m_count++;
print();
}
}
public:
QueueSolution()
{
init();
}
void run()
{
run(1);
cout << "Total: " << m_count << endl;
}
};
int main()
{
QueueSolution<8> qs;
qs.run();
return 0;
}我们来看看运行结果
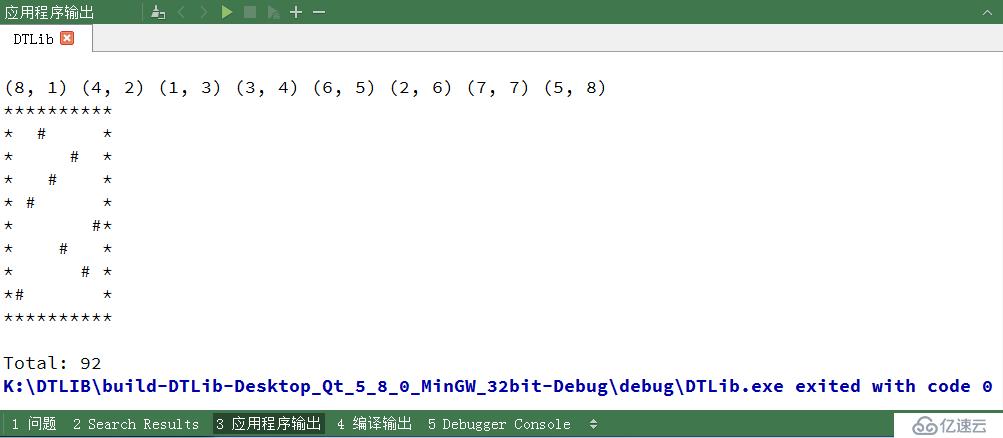
我们看到总共有 92 种解法。我们来看看四皇后,看看有多少种解法

我们看到总共有 2 种解法,如上图所示。通过今天对递归的学习,总结如下:1、程序运行后的栈存储区专供函数调用使用;2、栈存储区用于保存实参,局部变量,临时变量等;3、利用栈存储区能够方便的实现回溯算法;4、八皇后问题是栈回溯的经典应用。
免责声明:本站发布的内容(图片、视频和文字)以原创、转载和分享为主,文章观点不代表本网站立场,如果涉及侵权请联系站长邮箱:is@yisu.com进行举报,并提供相关证据,一经查实,将立刻删除涉嫌侵权内容。