您好,登录后才能下订单哦!
周一到周五,每天一篇,北京时间早上7点准时更新~
First, we do not pretend here that we will cover everything that is important for you to know(首先,我们不会在这里去涵盖所有对你来说很重要的东西). In fact, we will not even try to cover everything you should know(实际上,我们甚至都不会涵盖你应该知道的东西). In this chapter, we are just going to cover what you really need to know(在本章节,我们只是介绍一下那些你必须知道的东西). If you’re already a math whiz, you should skip immediately to the section ahead on the standard 3D transformations(如果你数学已经学的很好了,那么你应该跳过本段). Not only do you already know what we are about to cover, but most math fans will be somewhat offended that we did not give sufficient space to their favorite feature of homogeneous coordinate spaces(不仅仅是因为你已经知道了我们要介绍的东西,并且对于很多数学狂魔来说,他们会觉得本段根本连个屁都没说). Imagine one of those reality TV shows where you must escape a virtual swamp filled with crocodiles(想象一下综艺频道里那些从虚拟的充满了鳄鱼的沼泽里逃亡的游戏(这或许是作者自己看过的什么综艺节目,法克,谁能想象出来啊)). How much 3D math do you really need to know to survive(为了生存,你需要多少3D数学呢?)? That’s what the next two sections are going to be about—3D math survival skills(接下来的2个小段就是关于如何生存下来的3D数学). The crocodiles do not care if you really know what a homogeneous coordinate space is(如果你真的懂得齐次坐标的话,鳄鱼根本不在话下,分分钟可以吊打,当着它女朋友的面吃它的肉肉)
Vectors, or Which Way Is Which?(向量或者啥是啥?)
The main input to OpenGL is the vertex, which has a number of attributes that normally include a position(OpenGL的输入数据是vertex,它通常情况下都会包含位置这个属性). Basically, this is a position in xyz coordinate space, and a given position in space is defined by exactly one and only one unique xyz triplet(基本上这个位置在给定的某个空间里是唯一存在的). An xyz triplet, however, can be represented by a vector (in fact, for the mathematically pure of heart, a position is actually a vector too—there, we threw you a bone)(一个xyz的位置可以使用一个向量去表示). A vector is perhaps the single most important foundational concept to understand when it comes to manipulating 3D geometry(当俺们开始聊3D几何的时候,或许向量就是一个最重要的玩意了). Those three values (x, y, and z) combined represent two important values: a direction and a magnitude(向量的那三个值能表达两个非常重要的东西:方向和长度)
Figure 4.1 shows a point in space (picked arbitrarily) and an arrow drawn from the origin of the coordinate system to that point in space(图4.1展示了一个空间中的点以及一个从坐标系原点发出来,指向该点的一个箭头). The point can be thought of as a vertex when you are stitching together triangles, but the arrow can be thought of as a vector(这个点可以被当成是你去拼凑三角形的那些数据,然而这个箭头可以被看成是一个向量). A vector is first, and most simply, a direction from the origin toward a point in space(向量首先最简单的表达的是从原点指向一个点的方向). We use vectors all the time in OpenGL to represent directional quantities(我们总是在OpenGL里面使用向量去描述方向数据). For example, the x axis is the vector (1, 0, 0)(比如x轴的向量是(1,0,0)). This says to go positive one unit in the x direction, and zero in the y and z directions(意思是说,指向x轴正方向一个单位的距离以及y,z方向0个单位距离的地方). A vector is also how we point to where we are going—for example, which way is the camera pointing, or in which direction do we want to move to get away from that crocodile?(一个向量同样也被用来指向我们将要去哪里,比如摄像机指向哪里,还比如我们向哪个方向走来避开鳄鱼先生)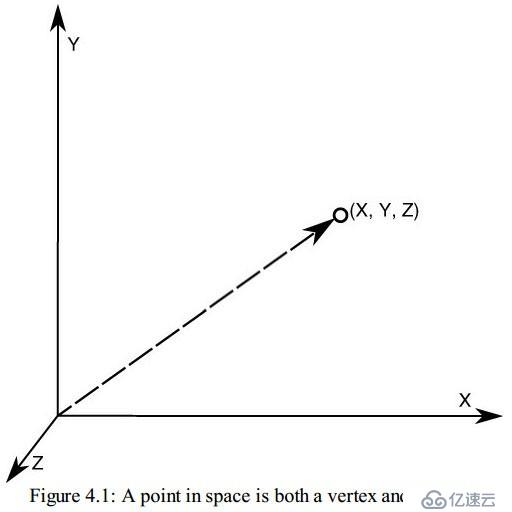
The vector is so fundamental to the operation of OpenGL that vectors of various sizes are first-class types in GLSL and are given names such as vec3 and vec4 (representing three- and four-element vectors, respectively)(向量是OpenGL中很多操作的基础,根据向量中数据个数的不同又分为N维向量,比如vec4、vec3这样子). The second quantity a vector can represent is the magnitude(向量能表达的第二个东西就是长度). The magnitude of a vector is the length of the vector(向量的magnitude就是指向量的长度,所以之前我们就直译成长度了,在国外混过的都知道这个基本概念). For our x-axis vector (1, 0, 0), the length of the vector is 1(对于我们x轴的向量来说,它的长度是1). A vector with a length of 1 we call a unit vector(长度只有1的向量叫做单位向量). If a vector is not a unit vector and we want to scale it to make it one, we call that normalization(如果一个向量的长度不是1,而我们想把它的长度变成1的话,这个过程叫做单位化). Normalizing a vector scales it such that its length becomes 1 and the vector is then said to be normalized(单位化一个向量会让它的长度变成1,变化完后,这个向量就可以被看成是已经被单位化鸟). Unit vectors are important when we want to represent only a direction and not a magnitude(当我们仅想表达一个方向,而不关心长度的时候,单位向量是很重要的). Also, if vector lengths appear in the equations we’ll be using, they get a whole lot simpler when those lengths are 1!(并且,当向量的长度是1的时候,我们在做向量运算的时候,总体来说会让情况变得更简单) A magnitude can be important as well; for example, it can tell us how far we need to move in a given direction—how far away we need to get from that crocodile(当然,向量的长度也很重要,比如,它可以告诉我们,沿着给定的方向,我们需要移动多少距离,才能避开我们的鳄鱼lady gaga们)
Vectors (and matrices) are such important concepts in 3D graphics that they are firstclass citizens in GLSL—the language in which you write your shaders(向量和矩阵是如此的重要,以至于当你在写shader的时候,他们是被GLSL原生的支持的). However, this is not so in languages like C++(然而,C++并不支持这货). To allow you to use them in your C++ programs, the vmath library, which is provided with this book’s source code, contains classes that can represent vectors and matrices that are named similarly to their GLSL counterparts(为了让你在C++程序里也能使用,俺写的vmath库将会提供这部分能力,它的命名和使用方式就是抄袭了GLSL里的). For instance, vmath::vec3 can represent a three-component floating-point vector (x, y, z), vmath::vec4 can represent a four-component floating-point vector (x, y, z, w), and so on(例如,vmath::vec3就可以表达3个浮点数组成的向量,vmath::vec4能表达四个浮点数组成的向量等等). The w coordinate is added to make the vector homogeneous but is typically set to 1.0(w分量使得向量变成了奇次向量,基本上这家伙的值就是1.0). The x, y, and z values might later be divided by w, which, when it is 1.0, essentially leaves the xyz values alone(x、y、z的值可能在后面会被w除,当它是1的时候,会保持xyz的值不变). The classes in vmath are actually templated classes with type definitions to represent common types such as single- and doubleprecision floating-point values, and signed- and unsigned-integer variables. (vmath是模板类,随便用就可以了,如果不清楚模板原理的可以观看东汉书院C++ Tricks课程,只要9块8,赶上书院正在举行老汉下乡,支持社会主义新农村建设,我们郑重承诺,买一送一! 买课程送壮妹一名,9块8买不到吃亏,9块8买不到上当,9块8你什么都买不到,哈哈哈哈。 不过说句正经的,尤其是需要写引擎内核的同学,让你站在深层次去看C++代码到底在干嘛,看完后对于如何使用别人的C++模板库是非常有帮助的。) vmath::vec3 and vmath::vec4 are defined simply as follows(vmath::vec3和vmath::vec4的定义如下)
typedef Tvec3 vec3;
typedef Tvec4 vec4;Declaring a three-component vector is as simple as(申明一个三维向量如下的例子如下)
vmath::vec3 vVector;If you include using namespace vmath; in your source code, you can even write(如果你直接把vmath的命名空间全部导入到你的项目中,你甚至可以像下面这样使用vmath)
vec3 vVector;However, in these examples, we’ll always qualify our use of the vmath library by explicitly using the vmath:: namespace(然而,在这些例子中,我们依然会显示的去使用vmath这个命名空间). All of the vmath classes define a number of constructors and copy operators, which means you can declare and initialize vectors as follows:(所有的vmath的类都定义了很多构造函数和拷贝的运算符,也就是说,你可以像下面如此这般来使用这个库)
vec3 vmath::vVertex1(0.0f, 0.0f, 1.0f);
vec4 vmath::vVertex2 = vec4(1.0f, 0.0f, 1.0f, 1.0f);
vec4 vmath::vVertex3(vVertex1, 1.0f);Now, an array of three-component vertices, such as for a triangle, can be declared as(一个三维的点可以被如下类似的代码定义:)
vec3 vmath::vVerts[] = { vmath::vec3(-0.5f, 0.0f, 0.0f),
vmath::vec3(0.5f, 0.0f, 0.0f),
vmath::vec3(0.0f, 0.5f, 0.0f) } ;This should look similar to the code that we introduced in the “Drawing Our First Triangle” section in Chapter 2(这个应该跟我们在第2章里画三角形时的那些代码长的很像,反正我是已经忘了第二章那个代码长啥样了). The vmath library also includes lots of math-related functions and overrides most operators on its class to allow vectors and matrices to be added, subtracted, multiplied, transposed, and so on(vmath库也包含了很多跟数学相关的函数并且重载了很多运算符,这样一来,那些个向量和矩阵就可以进行一些基本的运算操作了)
We need to be careful here not to gloss over that fourth w component too much(我们需要注意的是,别被w向量所吸引鸟). Most of the time when you specify geometry with vertex positions, a three-component vertex is all you want to store and send to OpenGL(大部分情况下,你需要表达一个几何形体的某个点的时候,三维向量就够了). For many directional vectors, such as a surface normal (a vector pointing perpendicular to a surface that is used for lighting calculations), a three-component vector suffices(对于很多方向向量,比如法线,三维向量就很够用了). However, we will soon delve into the world of matrices, and to transform a 3D vertex, you must multiply it by a 4 × 4 transformation matrix(当然,我们将很快进入矩阵的世界,并且,我们需要使用4x4的矩阵来对3D的点来进行操作). The rules are you must multiply a four-component vector by a 4 × 4 matrix(这里需要注意的是,你必须要用一个四维向量去与一个4x4的矩阵进行乘法操作); if you try and use a three-component vector with a 4 × 4 matrix, the crocodiles will eat you!(如果你用一个三维向量与一个4x4的矩阵进行配对,那些鳄鱼就会来吃你的大腿上的肉,就是我们在公众号里,那个人妖大腿内侧画了纹身的那一块肉) More on what all this means soon. Essentially, if you are going to do your own matrix operations on vectors, then you will probably want four-component vectors in many cases(更多的内容我们将会很快进行介绍。基本上,如果你希望使用矩阵对向量进行操作的时候,你将更多的会使用四维向量)
本日的翻译就到这里,明天见,拜拜~~
第一时间获取最新桥段,请关注东汉书院以及图形之心公众号
东汉书院,等你来玩哦
免责声明:本站发布的内容(图片、视频和文字)以原创、转载和分享为主,文章观点不代表本网站立场,如果涉及侵权请联系站长邮箱:is@yisu.com进行举报,并提供相关证据,一经查实,将立刻删除涉嫌侵权内容。