您好,登录后才能下订单哦!
密码登录
登录注册
点击 登录注册 即表示同意《亿速云用户服务条款》
我就废话不多说啦,直接上代码吧!
target = [1.5, 2.1, 3.3, -4.7, -2.3, 0.75]
prediction = [0.5, 1.5, 2.1, -2.2, 0.1, -0.5]
error = []
for i in range(len(target)):
error.append(target[i] - prediction[i])
print("Errors: ", error)
print(error)
squaredError = []
absError = []
for val in error:
squaredError.append(val * val)#target-prediction之差平方
absError.append(abs(val))#误差绝对值
print("Square Error: ", squaredError)
print("Absolute Value of Error: ", absError)
print("MSE = ", sum(squaredError) / len(squaredError))#均方误差MSE
from math import sqrt
print("RMSE = ", sqrt(sum(squaredError) / len(squaredError)))#均方根误差RMSE
print("MAE = ", sum(absError) / len(absError))#平均绝对误差MAE
targetDeviation = []
targetMean = sum(target) / len(target)#target平均值
for val in target:
targetDeviation.append((val - targetMean) * (val - targetMean))
print("Target Variance = ", sum(targetDeviation) / len(targetDeviation))#方差
print("Target Standard Deviation = ", sqrt(sum(targetDeviation) / len(targetDeviation)))#标准差
补充拓展:回归模型指标:MSE 、 RMSE、 MAE、R2
sklearn调用
# 测试集标签预测
y_predict = lin_reg.predict(X_test)
# 衡量线性回归的MSE 、 RMSE、 MAE、r2
from math import sqrt
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
print("mean_absolute_error:", mean_absolute_error(y_test, y_predict))
print("mean_squared_error:", mean_squared_error(y_test, y_predict))
print("rmse:", sqrt(mean_squared_error(y_test, y_predict)))
print("r2 score:", r2_score(y_test, y_predict))
原生实现
# 测试集标签预测
y_predict = lin_reg.predict(X_test)
# 衡量线性回归的MSE 、 RMSE、 MAE
mse = np.sum((y_test - y_predict) ** 2) / len(y_test)
rmse = sqrt(mse)
mae = np.sum(np.absolute(y_test - y_predict)) / len(y_test)
r2 = 1-mse/ np.var(y_test)
print("mse:",mse," rmse:",rmse," mae:",mae," r2:",r2)
相关公式
MSE
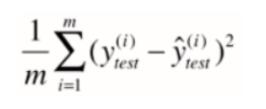
RMSE
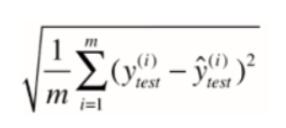
MAE
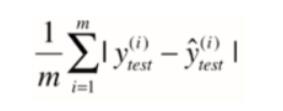
R2

以上这篇python之MSE、MAE、RMSE的使用就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持亿速云。
免责声明:本站发布的内容(图片、视频和文字)以原创、转载和分享为主,文章观点不代表本网站立场,如果涉及侵权请联系站长邮箱:is@yisu.com进行举报,并提供相关证据,一经查实,将立刻删除涉嫌侵权内容。