pytorch方法测试之归一化BatchNorm2d的示例分析

小编给大家分享一下pytorch方法测试之归一化BatchNorm2d的示例分析，相信大部分人都还不怎么了解，因此分享这篇文章给大家参考一下，希望大家阅读完这篇文章后大有收获，下面让我们一起去了解一下吧！

测试代码：

import torch

import torch.nn as nn

m = nn.BatchNorm2d(2,affine=True) #权重w和偏重将被使用
input = torch.randn(1,2,3,4)
output = m(input)

print("输入图片：")
print(input)
print("归一化权重：")
print(m.weight)
print("归一化的偏重：")
print(m.bias)

print("归一化的输出：")
print(output)
print("输出的尺度：")
print(output.size())

# i = torch.randn(1,1,2)
print("输入的第一个维度：")
print(input[0][0])
firstDimenMean = torch.Tensor.mean(input[0][0])
firstDimenVar= torch.Tensor.var(input[0][0],False) #Bessel's Correction贝塞尔校正不会被使用

print(m.eps)
print("输入的第一个维度平均值：")
print(firstDimenMean)
print("输入的第一个维度方差：")
print(firstDimenVar)

bacthnormone = \
  ((input[0][0][0][0] - firstDimenMean)/(torch.pow(firstDimenVar+m.eps,0.5) ))\
        * m.weight[0] + m.bias[0]
print(bacthnormone)

输出为：

输入图片：

tensor([[[[-2.4308, -1.0281, -1.1322, 0.9819],
     [-0.4069, 0.7973, 1.6296, 1.6797],
     [ 0.2802, -0.8285, 2.0101, 0.1286]],


     [[-0.5740, 0.1970, -0.7209, -0.7231],
     [-0.1489, 0.4993, 0.4159, 1.4238],
     [ 0.0334, -0.6333, 0.1308, -0.2180]]]])

归一化权重：

Parameter containing:
tensor([ 0.5653, 0.0322])

归一化的偏重：

Parameter containing:
tensor([ 0., 0.])

归一化的输出：

tensor([[[[-1.1237, -0.5106, -0.5561, 0.3679],
     [-0.2391, 0.2873, 0.6510, 0.6729],
     [ 0.0612, -0.4233, 0.8173, -0.0050]],


     [[-0.0293, 0.0120, -0.0372, -0.0373],
     [-0.0066, 0.0282, 0.0237, 0.0777],
     [ 0.0032, -0.0325, 0.0084, -0.0103]]]])

输出的尺度：

torch.Size([1, 2, 3, 4])

输入的第一个维度：

tensor([[-2.4308, -1.0281, -1.1322, 0.9819],
    [-0.4069, 0.7973, 1.6296, 1.6797],
    [ 0.2802, -0.8285, 2.0101, 0.1286]])
1e-05

输入的第一个维度平均值：

tensor(0.1401)

输入的第一个维度方差：

tensor(1.6730)
tensor(-1.1237)

结论：

输出的计算公式如下

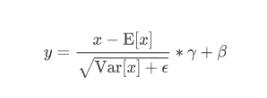
注意torch中方差实现的方法是没有使用Bessel's correction 贝塞尔校正的方差，所以在自己写的方差中不要用错了。

以上是“pytorch方法测试之归一化BatchNorm2d的示例分析”这篇文章的所有内容，感谢各位的阅读！相信大家都有了一定的了解，希望分享的内容对大家有所帮助，如果还想学习更多知识，欢迎关注亿速云行业资讯频道！