жӮЁеҘҪпјҢзҷ»еҪ•еҗҺжүҚиғҪдёӢи®ўеҚ•е“ҰпјҒ
жӯЈжҖҒеҲҶеёғеә”з”ЁжңҖе№ҝжіӣзҡ„иҝһз»ӯжҰӮзҺҮеҲҶеёғпјҢе…¶зү№еҫҒжҳҜвҖңй’ҹвҖқеҪўжӣІзәҝгҖӮиҝҷз§ҚеҲҶеёғзҡ„жҰӮзҺҮеҜҶеәҰеҮҪж•°дёәпјҡ
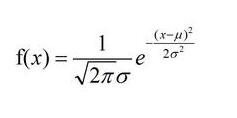
е…¶дёӯпјҢОјдёәеқҮеҖјпјҢПғдёәж ҮеҮҶе·®гҖӮ
жұӮжӯЈжҖҒеҲҶеёғжӣІзәҝдёӢйқўз§Ҝжңү3ПғеҺҹеҲҷ:
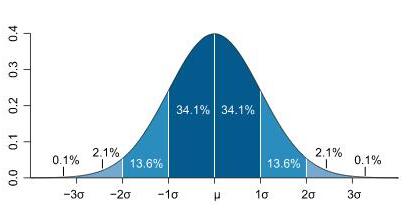
жӯЈжҖҒжӣІзәҝдёӢпјҢжЁӘиҪҙеҢәй—ҙпјҲОј-ПғпјҢОј+ПғпјүеҶ…зҡ„йқўз§Ҝдёә68.268949%пјҢжЁӘиҪҙеҢәй—ҙпјҲОј-1.96ПғпјҢОј+1.96ПғпјүеҶ…зҡ„йқўз§Ҝдёә95.449974%пјҢжЁӘиҪҙеҢәй—ҙпјҲОј-2.58ПғпјҢОј+2.58ПғпјүеҶ…зҡ„йқўз§Ҝдёә99.730020%гҖӮ
жұӮд»»ж„ҸеҢәй—ҙеҶ…жӣІзәҝдёӢзҡ„йқўз§ҜпјҢйҖҡеёёеҸҜд»Ҙеј•з”ЁscipyеҢ…дёӯзҡ„зӣёе…іеҮҪж•°
normеҮҪж•°з”ҹжҲҗдёҖдёӘз»ҷе®ҡеқҮеҖје’Ңж ҮеҮҶе·®зҡ„жӯЈжҖҒеҲҶеёғпјҢcdf(x)иЎЁзӨәпјҚвҲһеҲ°xзҡ„жҰӮзҺҮ
дҫӢпјҡ(2пјҢ1)жӯЈжҖҒеҲҶеёғдёӢ 2-3жӣІзәҝдёӢзҡ„йқўз§Ҝ
>>> import scipy.stats >>> scipy.stats.norm(2,1).cdf(3)-0.5 0.34134474606854293
з”ұдәҺжңүж—¶еҖҷдёҚдҫҝдәҺеј•з”ЁscipyеҢ…пјҢиҮӘзј–иҝҷдёҖеҮҪж•°д№ҹеҫҲз®ҖеҚ•
жұӮз§ҜеҲҶеҮҪж•°еҸӮиҖғпјҡеӨҚеҢ–жўҜеҪўжұӮз§ҜеҲҶ
cdfd(a,b,u,o)
a,b дёәеҢәй—ҙиө·е§ӢиҢғеӣҙпјҢuпјҢoеҲҶеҲ«дёәжӯЈжҖҒеҲҶеёғзҡ„еқҮеҖје’Ңж ҮеҮҶе·®гҖӮ
import math def pdf(x): return math.exp(-(x) ** 2 / (2)) / (math.sqrt(2 * math.pi)) def sum_fun_xk(xk, func): return sum([func(each) for each in xk]) def integral(a, b, n, func): h = (b - a)/float(n) xk = [a + i*h for i in range(1, n)] return h/2 * (func(a) + 2 * sum_fun_xk(xk, func) + func(b)) def cdfd(a,b,u,o): return integral((a-u)/o,(b-u)/o,10000,pdf) cdfd(2,3,2,1) Out: 0.3413399854638336
д»ҘдёҠиҝҷзҜҮPythonжұӮжӯЈжҖҒеҲҶеёғжӣІзәҝдёӢйқўз§Ҝе®һдҫӢе°ұжҳҜе°Ҹзј–еҲҶдә«з»ҷеӨ§е®¶зҡ„е…ЁйғЁеҶ…е®№дәҶпјҢеёҢжңӣиғҪз»ҷеӨ§е®¶дёҖдёӘеҸӮиҖғпјҢд№ҹеёҢжңӣеӨ§е®¶еӨҡеӨҡж”ҜжҢҒдәҝйҖҹдә‘гҖӮ
е…ҚиҙЈеЈ°жҳҺпјҡжң¬з«ҷеҸ‘еёғзҡ„еҶ…е®№пјҲеӣҫзүҮгҖҒи§Ҷйў‘е’Ңж–Үеӯ—пјүд»ҘеҺҹеҲӣгҖҒиҪ¬иҪҪе’ҢеҲҶдә«дёәдё»пјҢж–Үз« и§ӮзӮ№дёҚд»ЈиЎЁжң¬зҪ‘з«ҷз«ӢеңәпјҢеҰӮжһңж¶үеҸҠдҫөжқғиҜ·иҒ”зі»з«ҷй•ҝйӮ®з®ұпјҡis@yisu.comиҝӣиЎҢдёҫжҠҘпјҢ并жҸҗдҫӣзӣёе…іиҜҒжҚ®пјҢдёҖз»ҸжҹҘе®һпјҢе°Ҷз«ӢеҲ»еҲ йҷӨж¶үе«ҢдҫөжқғеҶ…е®№гҖӮ
жӮЁеҘҪпјҢзҷ»еҪ•еҗҺжүҚиғҪдёӢи®ўеҚ•е“ҰпјҒ