жӮЁеҘҪпјҢзҷ»еҪ•еҗҺжүҚиғҪдёӢи®ўеҚ•е“ҰпјҒ
дёҖгҖҒйўҳж„ҸзҗҶи§Ј
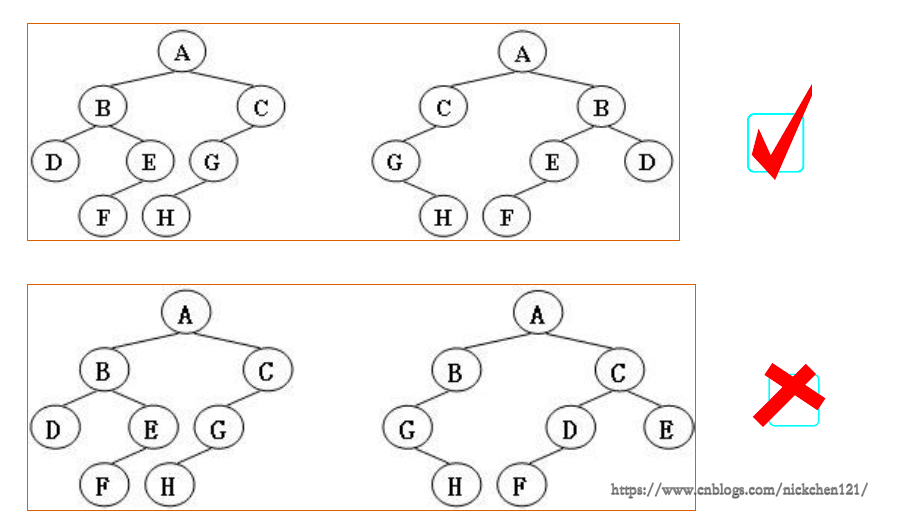
з»ҷе®ҡдёӨжЈөж ‘T1е’ҢT2гҖӮеҰӮжһңT1еҸҜд»ҘйҖҡиҝҮиӢҘе№Іж¬Ўе·ҰеҸіеӯ©еӯҗдә’жҚўе°ұеҸҳжҲҗT2пјҢеҲҷжҲ‘们称дёӨжЈөж ‘жҳҜвҖңеҗҢжһ„зҡ„вҖқгҖӮзҺ°з»ҷе®ҡдёӨжЈөж ‘пјҢиҜ·дҪ еҲӨж–ӯе®ғ们жҳҜеҗҰжҳҜеҗҢжһ„зҡ„гҖӮ
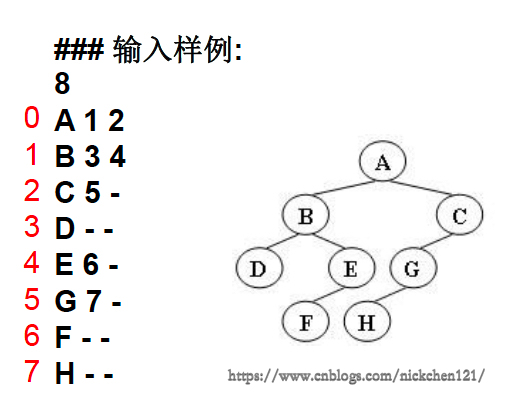
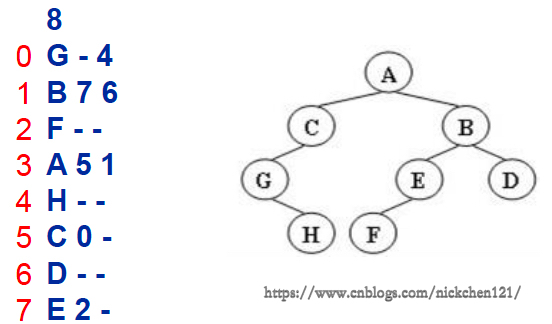
иҫ“е…Ҙж јејҸпјҡиҫ“е…Ҙз»ҷеҮә2жЈөдәҢеҸүж ‘зҡ„дҝЎжҒҜпјҡ
е…ҲеңЁдёҖиЎҢдёӯз»ҷеҮәиҜҘж ‘зҡ„з»“зӮ№ж ‘пјҢйҡҸеҗҺNиЎҢ
第iиЎҢеҜ№еә”зј–еҸ·з¬¬iдёӘз»“зӮ№пјҢз»ҷеҮәиҜҘз»“зӮ№дёӯеӯҳеӮЁзҡ„еӯ—жҜҚгҖҒе…¶е·Ұеӯ©еӯҗз»“зӮ№зҡ„зј–еҸ·гҖҒеҸіеӯ©еӯҗз»“зӮ№зҡ„зј–еҸ·
еҰӮжһңеӯ©еӯҗз»“зӮ№дёәз©әпјҢеҲҷеңЁзӣёеә”дҪҚзҪ®з»ҷеҮәвҖң-вҖқ
еҰӮдёӢеӣҫжүҖзӨәпјҢжңүеӨҡз§ҚиЎЁзӨәзҡ„ж–№ејҸпјҢжҲ‘们еҲ—еҮәд»ҘдёӢдёӨз§Қпјҡ
дәҢгҖҒжұӮи§ЈжҖқи·Ҝ
жҗңеҲ°дёҖзҜҮд№ҹжҳҜи®ІиҝҷдёӘзҡ„пјҢдҪҶжҳҜйӮЈзҜҮ并没жңүе®Ңе…Ёз”ЁеҲ°еҚ•еҗ‘й“ҫиЎЁзҡ„ж–№жі•пјҢжүҖд»Ҙз ”з©¶дәҶдёҖдёӢпјҢеҶҷдәҶдёҖдёӘжҳҜе®Ңе…Ёз”ЁеҚ•еҗ‘й“ҫиЎЁзҡ„ж–№жі•пјҡ
е…¶е®һеә”иҜҘжңүжӣҙдјҳйӣ…зҡ„еҲ йҷӨж•ҙдёӘеҚ•еҗ‘еҲ—иЎЁзҡ„ж–№жі•пјҢжҜ”еҰӮеӨҙи®ҫдёәnoneпјҢеҸҜиғҪдјҡж”№иҝӣдёӢпјҹ
# pythonиҜӯиЁҖе®һзҺ°
L1 = list(map(int, input().split()))
L2 = list(map(int, input().split()))
# иҠӮзӮ№
class Node:
def __init__(self, coef, exp):
self.coef = coef
self.exp = exp
self.next = None
# еҚ•й“ҫиЎЁ
class List:
def __init__(self, node=None):
self.__head = node
# дёәдәҶи®ҝй—®з§Ғжңүзұ»
def gethead(self):
return self.__head
def travel(self):
cur1 = self.__head
cur2 = self.__head
if cur1.next != None:
cur1 = cur1.next
else:
print(cur2.coef, cur2.exp, end="")
return
while cur1.next != None:
print(cur2.coef, cur2.exp, end=" ")
cur1 = cur1.next
cur2 = cur2.next
print(cur2.coef, cur2.exp, end=" ")
cur2 = cur2.next
print(cur2.coef, cur2.exp, end="")
# add item in the tail
def append(self, coef, exp):
node = Node(coef, exp)
if self.__head == None:
self.__head = node
else:
cur = self.__head
while cur.next != None:
cur = cur.next
cur.next = node
def addl(l1, l2):
p1 = l1.gethead()
p2 = l2.gethead()
l3 = List()
while (p1 is not None) & (p2 is not None):
if (p1.exp > p2.exp):
l3.append(p1.coef, p1.exp)
p1 = p1.next
elif (p1.exp < p2.exp):
l3.append(p2.coef, p2.exp)
p2 = p2.next
else:
if (p1.coef + p2.coef == 0):
p1 = p1.next
p2 = p2.next
else:
l3.append(p2.coef + p1.coef, p1.exp)
p2 = p2.next
p1 = p1.next
while p1 is not None:
l3.append(p1.coef, p1.exp)
p1 = p1.next
while p2 is not None:
l3.append(p2.coef, p2.exp)
p2 = p2.next
if l3.gethead() == None:
l3.append(0, 0)
return l3
def mull(l1, l2):
p1 = l1.gethead()
p2 = l2.gethead()
l3 = List()
l4 = List()
if (p1 is not None) & (p2 is not None):
while p1 is not None:
while p2 is not None:
l4.append(p1.coef * p2.coef, p1.exp + p2.exp)
p2 = p2.next
l3 = addl(l3, l4)
l4 = List()
p2 = l2.gethead()
p1 = p1.next
else:
l3.append(0, 0)
return l3
def L2l(L):
l = List()
L.pop(0)
for i in range(0, len(L), 2):
l.append(L[i], L[i + 1])
return l
l1 = L2l(L1)
l2 = L2l(L2)
l3 = List()
l3 = mull(l1, l2)
l3.travel()
print("")
l3 = List()
l3 = addl(l1, l2)
l3.travel()
д»ҘдёҠе°ұжҳҜжң¬ж¬Ўд»Ӣз»Қзҡ„е…ЁйғЁеҶ…е®№зҹҘиҜҶзӮ№пјҢзӣёе…іеҶ…е®№еҸҜд»ҘеҸӮйҳ…дёӢж–№зҹҘиҜҶзӮ№пјҢж„ҹи°ўеӨ§е®¶еҜ№дәҝйҖҹдә‘зҡ„ж”ҜжҢҒгҖӮ
е…ҚиҙЈеЈ°жҳҺпјҡжң¬з«ҷеҸ‘еёғзҡ„еҶ…е®№пјҲеӣҫзүҮгҖҒи§Ҷйў‘е’Ңж–Үеӯ—пјүд»ҘеҺҹеҲӣгҖҒиҪ¬иҪҪе’ҢеҲҶдә«дёәдё»пјҢж–Үз« и§ӮзӮ№дёҚд»ЈиЎЁжң¬зҪ‘з«ҷз«ӢеңәпјҢеҰӮжһңж¶үеҸҠдҫөжқғиҜ·иҒ”зі»з«ҷй•ҝйӮ®з®ұпјҡis@yisu.comиҝӣиЎҢдёҫжҠҘпјҢ并жҸҗдҫӣзӣёе…іиҜҒжҚ®пјҢдёҖз»ҸжҹҘе®һпјҢе°Ҷз«ӢеҲ»еҲ йҷӨж¶үе«ҢдҫөжқғеҶ…е®№гҖӮ
жӮЁеҘҪпјҢзҷ»еҪ•еҗҺжүҚиғҪдёӢи®ўеҚ•е“ҰпјҒ