жӮЁеҘҪпјҢзҷ»еҪ•еҗҺжүҚиғҪдёӢи®ўеҚ•е“ҰпјҒ
е°Ҹзј–з»ҷеӨ§е®¶еҲҶдә«дёҖдёӢеҰӮдҪ•дҪҝз”ЁpythonеҲҶжІ»жі•жұӮдәҢз»ҙж•°з»„еұҖйғЁеі°еҖјпјҢеёҢжңӣеӨ§е®¶йҳ…иҜ»е®ҢиҝҷзҜҮж–Үз« д№ӢеҗҺйғҪжңүжүҖ收иҺ·пјҢдёӢйқўи®©жҲ‘们дёҖиө·еҺ»жҺўи®Ёеҗ§пјҒ
йўҳзӣ®зҡ„ж„ҸжҖқеӨ§иҮҙжҳҜеңЁдёҖдёӘn*mзҡ„дәҢз»ҙж•°з»„дёӯпјҢжүҫеҲ°дёҖдёӘеұҖйғЁеі°еҖјгҖӮеі°еҖјиҰҒжұӮеӨ§дәҺзӣёйӮ»зҡ„еӣӣдёӘе…ғзҙ пјҲж•°з»„иҫ№з•Ңд»ҘеӨ–и§Ҷдёәиҙҹж— з©·пјүпјҢжҜ”еҰӮжңҖеҗҺжҲ‘们жүҫеҲ°еі°еҖјA[j][i]пјҢеҲҷжңүA[j][i] > A[j+1][i] && A[j][i] > A[j-1][i] && A[j][i] > A[j][i+1] && A[j][i] > A[j][i-1]гҖӮиҝ”еӣһиҜҘеі°еҖјзҡ„еқҗж Үе’ҢеҖјгҖӮ
еҪ“然пјҢжңҖз®ҖеҚ•зӣҙжҺҘзҡ„ж–№жі•е°ұжҳҜйҒҚеҺҶжүҖжңүж•°з»„е…ғзҙ пјҢеҲӨж–ӯжҳҜеҗҰдёәеі°еҖјпјҢж—¶й—ҙеӨҚжқӮеәҰдёәO(n^2)
еҶҚдјҳеҢ–дёҖзӮ№жұӮжҜҸдёҖиЎҢпјҲеҲ—пјүзҡ„жңҖеӨ§еҖјпјҢеҶҚйҖҡиҝҮдәҢеҲҶжі•жүҫжңҖеӨ§еҖјеҲ—зҡ„еі°еҖјпјҲе…·дҪ“ж–№жі•еҸҜи§ҒдёҖз»ҙж•°з»„жұӮеі°еҖјпјүпјҢиҝҷз§Қз®—жі•ж—¶й—ҙеӨҚжқӮеәҰдёәO(logn)
иҝҷйҮҢи®Ёи®әзҡ„жҳҜдёҖз§ҚеӨҚжқӮеәҰдёәO(n)зҡ„з®—жі•пјҢз®—жі•жҖқи·ҜеҲҶдёәд»ҘдёӢеҮ жӯҘпјҡ
1гҖҒжүҫвҖңз”°вҖқеӯ—гҖӮеҢ…жӢ¬еӨ–еӣҙзҡ„еӣӣжқЎиҫ№е’Ңдёӯй—ҙжЁӘз«–дёӨжқЎиҫ№пјҲеӣҫдёӯз»ҝиүІйғЁеҲҶпјүпјҢжҜ”иҫғе…¶еӨ§е°ҸпјҢжүҫеҲ°жңҖеӨ§еҖјзҡ„дҪҚзҪ®гҖӮпјҲеӣҫдёӯзҡ„7пјү
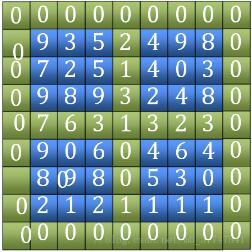
2гҖҒжүҫеҲ°з”°еӯ—дёӯжңҖеӨ§еҖјеҗҺпјҢеҲӨж–ӯе®ғжҳҜдёҚжҳҜеұҖйғЁеі°еҖјпјҢеҰӮжһңжҳҜиҝ”еӣһиҜҘеқҗж ҮпјҢеҰӮжһңдёҚжҳҜпјҢи®°еҪ•жүҫеҲ°зӣёйӮ»еӣӣдёӘзӮ№дёӯжңҖеӨ§еҖјеқҗж ҮгҖӮйҖҡиҝҮиҜҘеқҗж ҮжүҖеңЁзҡ„иұЎйҷҗзј©е°ҸиҢғеӣҙпјҢ继з»ӯжҜ”иҫғдёӢдёҖдёӘз”°еӯ—
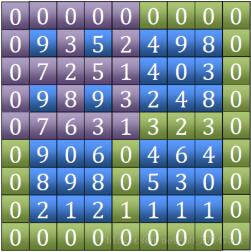
3гҖҒеҪ“иҢғеӣҙзј©е°ҸеҲ°3*3ж—¶еҝ…е®ҡдјҡжүҫеҲ°еұҖйғЁеі°еҖјпјҲд№ҹеҸҜиғҪд№ӢеүҚе°ұжүҫеҲ°дәҶпјү
е…ідәҺдёәд»Җд№ҲжҲ‘们йҖүжӢ©зҡ„иҢғеӣҙеҶ…дёҖе®ҡеӯҳеңЁеі°еҖјпјҢеӨ§е®¶еҸҜд»Ҙиҝҷж ·жғіпјҢйҰ–е…ҲжҲ‘们жңүдёҖдёӘеңҲпјҢжҲ‘们已зҹҘжңүеңҲеҶ…иҮіе°‘жңүдёҖдёӘе…ғзҙ еӨ§дәҺиҝҷдёӘеңҲжүҖжңүзҡ„е…ғзҙ пјҢйӮЈд№ҲпјҢжҳҜдёҚжҳҜиҝҷдёӘеңҲдёӯдёҖе®ҡжңүдёҖдёӘжңҖеӨ§еҖјпјҹ
еҸҜиғҪиҜҙеҫ—жңүзӮ№з»•пјҢдҪҶжҳҜеӨҡжғіжғіеә”иҜҘиғҪеӨҹзҗҶи§ЈпјҢд№ҹеҸҜд»Ҙз”Ёж•°еӯҰзҡ„еҸҚиҜҒжі•жқҘиҜҒжҳҺгҖӮ
з®—жі•жҲ‘们зҗҶи§ЈеҗҺжҺҘдёӢжқҘе°ұжҳҜд»Јз Ғе®һзҺ°дәҶпјҢиҝҷйҮҢжҲ‘з”Ёзҡ„иҜӯиЁҖжҳҜpythonпјҲеҲқеӯҰpythonпјҢеҸҜиғҪжңүдәӣз”Ёжі•дёҠдёҚеӨҹз®ҖжҙҒиҜ·и§Ғи°…пјүпјҢе…ҲдёҠд»Јз Ғпјҡ
import numpy as np
def max_sit(*n): #иҝ”еӣһжңҖеӨ§е…ғзҙ зҡ„дҪҚзҪ®
temp = 0
sit = 0
for i in range(len(n)):
if(n[i]>temp):
temp = n[i]
sit = i
return sit
def dp(s1,s2,e1,e2):
m1 = int((e1-s1)/2)+s1 #row
m2 = int((e2-s1)/2)+s2 #col
nub = e1-s1
temp = 0
sit_row = 0
sit_col = 0
for i in range(nub):
t = max_sit(list[s1][s2+i], #第дёҖжҺ’
list[m1][s2+i], #дёӯй—ҙжҺ’
list[e1][s2+i], #жңҖеҗҺжҺ’
list[s1+i][s2], #第дёҖеҲ—
list[s1+i][m2], #дёӯй—ҙеҲ—
list[s1+i][e2], #жңҖеҗҺеҲ—
temp)
if(t==6):
pass
elif(t==0):
temp = list[s1][s2+i]
sit_row = s1
sit_col = s2+i
elif(t==1):
temp = list[m1][s2+i]
sit_row = m1
sit_col = s2+i
elif(t==2):
temp = list[e1][s2+i]
sit_row = e1
sit_col = s2+i
elif(t==3):
temp = list[s1+i][s2]
sit_row = s1+i
sit_row = s2
elif(t==4):
temp = list[s1+i][m2]
sit_row = s1+i
sit_col = m2
elif(t==5):
temp = list[s1+i][e2]
sit_row = s1+i
sit_col = m2
t = max_sit(list[sit_row][sit_col], #дёӯ
list[sit_row-1][sit_col], #дёҠ
list[sit_row+1][sit_col], #дёӢ
list[sit_row][sit_col-1], #е·Ұ
list[sit_row][sit_col+1]) #еҸі
if(t==0):
return [sit_row-1,sit_col-1]
elif(t==1):
sit_row-=1
elif(t==2):
sit_row+=1
elif(t==3):
sit_col-=1
elif(t==4):
sit_col+=1
if(sit_row<m1):
e1 = m1
else:
s1 = m1
if(sit_col<m2):
e2 = m2
else:
s2 = m2
return dp(s1,s2,e1,e2)
f = open("demo.txt","r")
list = f.read()
list = list.split("\n") #еҜ№иЎҢиҝӣиЎҢеҲҮзүҮ
list = ["0 "*len(list)]+list+["0 "*len(list)] #еҠ дёҠдёӢзҡ„еӣҙеўҷ
for i in range(len(list)): #еҜ№еҲ—иҝӣиЎҢеҲҮзүҮ
list[i] = list[i].split()
list[i] = ["0"]+list[i]+["0"] #еҠ е·ҰеҸізҡ„еӣҙеўҷ
list = np.array(list).astype(np.int32)
row_n = len(list)
col_n = len(list[0])
ans_sit = dp(0,0,row_n-1,col_n-1)
print("жүҫеҲ°еі°еҖјзӮ№дҪҚдәҺпјҡ",ans_sit)
print("иҜҘеі°еҖјзӮ№еӨ§е°Ҹдёәпјҡ",list[ans_sit[0]+1,ans_sit[1]+1])
f.close()йҰ–е…ҲжҲ‘зҡ„иҫ“е…ҘеҶҷеңЁtxtж–Үжң¬ж–Ү件йҮҢпјҢйҖҡиҝҮеӯ—з¬ҰдёІиҪ¬жҚўеҸҳдёәдәҢз»ҙж•°з»„пјҢе…·дҪ“иҪ¬жҚўиҝҮзЁӢеҸҜд»ҘзңӢжҲ‘дёҠдёҖзҜҮеҚҡе®ўвҖ”вҖ”pythonдёӯеӯ—з¬ҰдёІиҪ¬жҚўдёәдәҢз»ҙж•°з»„гҖӮпјҲйңҖиҰҒжіЁж„Ҹзҡ„жҳҜеҰӮжһңеңЁwindowsзҺҜеўғдёӯsplitеҗҺзҡ„еҲ—иЎЁжІЎжңүз©әе°ҫе·ҙпјҢжүҖд»ҘдёҚз”ЁеҠ list.pop()иҝҷеҸҘиҜқпјүгҖӮжңүзҡ„еҸҳеҠЁжҳҜжҲ‘еңЁдәҢз»ҙж•°з»„еӣӣе‘ЁеҠ дәҶвҖң0вҖқзҡ„еӣҙеўҷгҖӮеҠ еӣҙеўҷеҸҜд»ҘеҶҚжҲ‘们еҲӨж–ӯеі°еҖјзҡ„ж—¶еҖҷдёҚз”ЁиҖғиҷ‘иҫ№з•Ңй—®йўҳгҖӮ
max_sit(*n)еҮҪж•°з”ЁдәҺжүҫеҲ°еӨҡдёӘеҖјдёӯжңҖеӨ§еҖјзҡ„дҪҚзҪ®пјҢиҝ”еӣһе…¶дҪҚзҪ®пјҢpythonзҡ„еҶ…жһ„зҡ„maxеҮҪж•°еҸӘиғҪиҝ”еӣһжңҖеӨ§еҖјпјҢжүҖд»ҘиҝҳжҳҜйңҖиҰҒиҮӘе·ұеҶҷпјҢ*nиЎЁзӨәдёҚе®ҡй•ҝеҸӮж•°пјҢеӣ дёәжҲ‘йңҖиҰҒеңЁжҜ”иҫғз”°е’ҢеҚҒпјҲеҲӨж–ӯеі°еҖјпјүйғҪз”ЁеҲ°иҝҷдёӘеҮҪж•°
def max_sit(*n): #иҝ”еӣһжңҖеӨ§е…ғзҙ зҡ„дҪҚзҪ® temp = 0 sit = 0 for i in range(len(n)): if(n[i]>temp): temp = n[i] sit = i return sit
dp(s1,s2,e1,e2)еҮҪж•°дёӯеӣӣдёӘеҸӮж•°зҡ„еҲҶеҲ«еҸҜзңӢдёәstartxпјҢstartyпјҢendxпјҢendyгҖӮеҚіжҲ‘们жҹҘжүҫиҢғеӣҙе·ҰдёҠи§’е’ҢеҸідёӢи§’зҡ„еқҗж ҮеҖјгҖӮ
m1,m2еҲҶеҲ«жҳҜrow е’Ңcolзҡ„дёӯй—ҙеҖјпјҢд№ҹе°ұжҳҜз”°еӯ—зҡ„дёӯй—ҙгҖӮ
def dp(s1,s2,e1,e2): m1 = int((e1-s1)/2)+s1 #row m2 = int((e2-s1)/2)+s2 #col
дҫқж¬ЎжҜ”иҫғ3иЎҢ3еҲ—дёӯзҡ„еҖјжүҫеҲ°жңҖеӨ§еҖјпјҢжіЁж„ҸиҝҷйҮҢиҰҒжұӮдәҢз»ҙж•°з»„дёәжӯЈж–№еҪўпјҢеҰӮжһңдёәзҹ©еҪўйңҖиҰҒеҒҡи°ғж•ҙ
for i in range(nub): t = max_sit(list[s1][s2+i], #第дёҖжҺ’ list[m1][s2+i], #дёӯй—ҙжҺ’ list[e1][s2+i], #жңҖеҗҺжҺ’ list[s1+i][s2], #第дёҖеҲ— list[s1+i][m2], #дёӯй—ҙеҲ— list[s1+i][e2], #жңҖеҗҺеҲ— temp) if(t==6): pass elif(t==0): temp = list[s1][s2+i] sit_row = s1 sit_col = s2+i elif(t==1): temp = list[m1][s2+i] sit_row = m1 sit_col = s2+i elif(t==2): temp = list[e1][s2+i] sit_row = e1 sit_col = s2+i elif(t==3): temp = list[s1+i][s2] sit_row = s1+i sit_row = s2 elif(t==4): temp = list[s1+i][m2] sit_row = s1+i sit_row = m2 elif(t==5): temp = list[s1+i][e2] sit_row = s1+i sit_row = m2
еҲӨж–ӯз”°еӯ—дёӯжңҖеӨ§еҖјжҳҜдёҚжҳҜеі°еҖјпјҢ并жүҫдёҚеҮәзӣёйӮ»жңҖеӨ§еҖј
t = max_sit(list[sit_row][sit_col], #дёӯ list[sit_row-1][sit_col], #дёҠ list[sit_row+1][sit_col], #дёӢ list[sit_row][sit_col-1], #е·Ұ list[sit_row][sit_col+1]) #еҸі if(t==0): return [sit_row-1,sit_col-1] elif(t==1): sit_row-=1 elif(t==2): sit_row+=1 elif(t==3): sit_col-=1 elif(t==4): sit_col+=1
зј©е°ҸиҢғеӣҙпјҢйҖ’еҪ’жұӮи§Ј
if(sit_row<m1): e1 = m1 else: s1 = m1 if(sit_col<m2): e2 = m2 else: s2 = m2 return dp(s1,s2,e1,e2)
еҘҪдәҶпјҢеҲ°иҝҷйҮҢд»Јз Ғеҹәжң¬еҲҶжһҗе®ҢдәҶгҖӮеҰӮжһңиҝҳжңүдёҚжё…жҘҡзҡ„ең°ж–№ж¬ўиҝҺдёӢж–№з•ҷиЁҖгҖӮ
йҷӨдәҶиҝҷз§Қз®—жі•еӨ–пјҢжҲ‘д№ҹеҶҷдёҖз§ҚиҙӘеҝғз®—жі•жқҘжұӮи§ЈиҝҷйҒ“йўҳпјҢеҸӘеҸҜжғңжңҖеқҸзҡ„жғ…еҶөдёӢз®—жі•еӨҚжқӮеәҰиҝҳжҳҜO(n^2),QAQгҖӮ
еӨ§дҪ“зҡ„жҖқи·Ҝе°ұжҳҜд»Һдёӯй—ҙдҪҚзҪ®иө·жүҫзӣёйӮ»4дёӘзӮ№дёӯжңҖеӨ§зҡ„зӮ№пјҢ继з»ӯжҠҠиҜҘзӮ№жқҘжүҫзӣёйӮ»жңҖеӨ§зӮ№пјҢжңҖеҗҺдёҖе®ҡдјҡжүҫеҲ°дёҖдёӘеі°еҖјзӮ№пјҢжңүе…ҙи¶Јзҡ„еҸҜд»ҘзңӢдёҖдёӢпјҢдёҠд»Јз Ғпјҡ
#!/usr/bin/python3
def dp(n):
temp = (str[n],str[n-9],str[n-1],str[n+1],str[n+9]) #дёӯ дёҠ е·Ұ еҸі дёӢ
sit = temp.index(max(temp))
if(sit==0):
return str[n]
elif(sit==1):
return dp(n-9)
elif(sit==2):
return dp(n-1)
elif(sit==3):
return dp(n+1)
else:
return dp(n+9)
f = open("/home/nancy/жЎҢйқў/demo.txt","r")
list = f.read()
list = list.replace(" ","").split() #иҪ¬жҚўдёәеҲ—иЎЁ
row = len(list)
col = len(list[0])
str="0"*(col+3)
for x in list: #еҠ еӣҙеўҷ дәҢз»ҙеҸҳдёҖз»ҙ
str+=x+"00"
str+="0"*(col+1)
mid = int(len(str)/2)
print(str,mid)
p = dp(mid)
print (p)
f.close()зңӢе®ҢдәҶиҝҷзҜҮж–Үз« пјҢзӣёдҝЎдҪ еҜ№вҖңеҰӮдҪ•дҪҝз”ЁpythonеҲҶжІ»жі•жұӮдәҢз»ҙж•°з»„еұҖйғЁеі°еҖјвҖқжңүдәҶдёҖе®ҡзҡ„дәҶи§ЈпјҢеҰӮжһңжғідәҶи§ЈжӣҙеӨҡзӣёе…ізҹҘиҜҶпјҢж¬ўиҝҺе…іжіЁдәҝйҖҹдә‘иЎҢдёҡиө„и®Ҝйў‘йҒ“пјҢж„ҹи°ўеҗ„дҪҚзҡ„йҳ…иҜ»пјҒ
е…ҚиҙЈеЈ°жҳҺпјҡжң¬з«ҷеҸ‘еёғзҡ„еҶ…е®№пјҲеӣҫзүҮгҖҒи§Ҷйў‘е’Ңж–Үеӯ—пјүд»ҘеҺҹеҲӣгҖҒиҪ¬иҪҪе’ҢеҲҶдә«дёәдё»пјҢж–Үз« и§ӮзӮ№дёҚд»ЈиЎЁжң¬зҪ‘з«ҷз«ӢеңәпјҢеҰӮжһңж¶үеҸҠдҫөжқғиҜ·иҒ”зі»з«ҷй•ҝйӮ®з®ұпјҡis@yisu.comиҝӣиЎҢдёҫжҠҘпјҢ并жҸҗдҫӣзӣёе…іиҜҒжҚ®пјҢдёҖз»ҸжҹҘе®һпјҢе°Ҷз«ӢеҲ»еҲ йҷӨж¶үе«ҢдҫөжқғеҶ…е®№гҖӮ
жӮЁеҘҪпјҢзҷ»еҪ•еҗҺжүҚиғҪдёӢи®ўеҚ•е“ҰпјҒ