您好,登录后才能下订单哦!
最近刚学习算法设计与分析的课程,所用教材是清华大学出版社王晓东编著的《算法设计与分析》。一道关于递归与分治算法的练习题如下:
刚拿到题目觉得这题目似乎和递归分治没有什么关系,但是O(1)的空间复杂度,以及O(n)的时间复杂度度就限制了解决方法,也就是分治和递归。(使用python语言只需几行,用切片即可完成,这里附上极其弱智的代码)
def exchange(a,k):
a=a[k:]+a[0:k]#列表切片
return a
ls=[1,2,3,4,5,6,7]
print(exchange(ls,4))
现在我们来思考这个递归分治算法。
开始前先说明一下变量含义:
start:左边子数组开始位置下标
sep:分割位置下标(左边子数组结束位置下标)
end:右边子数组结束位置下标
首先,是最简单的情况,相信大家一定能想到,如果两个子数组长度相等,直接遍历子数组的长度,写上三行交换代码就可以解决了。(在这就不给出图例了,简单脑补一下即可)
接下来,就是剩余两种情况:分别是左边子数组长度>右边子数组长度以及左边子数组长度<右边子数组长度。我的基本想法就是长度小的一边可以直接交换到位,长度长的一边分成两部分,一部分就是长度短的子数组长度,另一部分就是剩余部分长度。即:
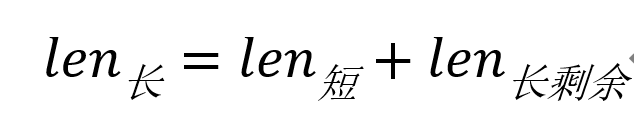
长数组用和短数组相同长度的元素和短数组元素一一交换,长数组剩余元素不动。第一次交换完成后短数组已经直接到位,接下来处理剩余元素长度即可,从而问题规模缩小,使用分治递归可以解决。
下面图例都是以这个数组为例{1,2,3,4,5,6,7}(红色字体表示已经到位的元素)
图一(start=0,sep=4,end=6):
判断是左边大于右边;长度为2的两对交换。1,2和6,7互换位置;6,7到位。start前进2位(start=2),sep不变,end也不变。
判断是左边大于右边;1,2和6,7互换位置;6,7,1,2到位。start再前进2位(start=4),sep不变,end也不变。
判断是左边小于右边;5和3互换位置;6,7,1,2,3到位。start前进1位(start=5),sep增1(sep=5),end不变。
判断是左边等于右边;5和4直接交换位置,所有元素全部到位。
图二(start=0,sep=1,end=6):
判断是左边小于右边;长度为2的两对交换。1,2和3,4互换位置;3,4到位。start前进2位(start=2),sep前进1位(sep=3),end也不变。
判断是左边小于右边;1,2和5,6互换位置;3,4,5,6到位。start再前进2位(start=4),sep前进2位(sep=5),end也不变。
判断是左边大于右边;5和3互换位置;6,7,1,2,3到位。start前进1位(start=5),sep增1(sep=5),end不变。
判断是左边等于右边;2和1直接交换位置,所有元素全部到位。
接下来是代码呈现:
public static void exchange(int a[],int start,int sep,int end)
{ 郑州妇科医院 http://www.zyfuke.com/
int t;
// 左边子数组长度 = 右边子数组长度
if(end-sep==sep-start+1)
{
for (int i = start; i <=sep; i++)
{
t=a[i];
a[i]=a[i+sep-start+1];
a[i+sep-start+1]=t;
}
}
// 左边子数组长度 > 右边子数组长度
if(end-sep
{
for(int i=end;i>=sep+1;i--)
{
t=a[i];
a[i]=a[i-(sep-start+1)];
a[i-(sep-start+1)]=t;
}
// start=start+end-sep;
exchange(a, start+end-sep, sep, end);
//递归调用exchange方法
// exchange(a, start, sep, end);
}
// 左边子数组长度 < 右边子数组长度
if(end-sep>sep-start+1)
{
for(int i=start;i<=sep;i++)
{
t=a[i];
a[i]=a[i+sep-start+1];
a[i+sep-start+1]=t;
}
// start=sep+1;
// sep=sep+sep-start+1;
exchange(a, sep+1, sep+sep-start+1, end);
//递归调用exchange方法
exchange(a, start, sep, end);
}
}
左边子数组长度 >右边子数组长度:
左右两边交换,中间不动,交换后左边部分完成,右边递归,*start前进短的子数组的长度个单位,*短的子数组长度=end-sep,所以有start=start+end-sep;sep不变,end也不变。
左边子数组长度 <右边子数组长度:
左边中间交换,右边不动,交换后左边部分完成,右边递归,start前进短的子数组的长度个单位,短的子数组长度=sep-start+1,所以有start=start+sep-start+1=sep+1。sep也前进短子数组长度个单位,sep=sep+sep-start+1;end不变。
测试:
int a[]= {10,2,8,3,5,4,7,1};
...
exchange(a, 0,4,a.length-1);
免责声明:本站发布的内容(图片、视频和文字)以原创、转载和分享为主,文章观点不代表本网站立场,如果涉及侵权请联系站长邮箱:is@yisu.com进行举报,并提供相关证据,一经查实,将立刻删除涉嫌侵权内容。