您好,登录后才能下订单哦!
使用python 实现一个贪心算法?相信很多没有经验的人对此束手无策,为此本文总结了问题出现的原因和解决方法,通过这篇文章希望你能解决这个问题。
贪心算法
贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的是在某种意义上的局部最优解。
贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择,选择的贪心策略必须具备无后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关。
基本思路
思想
贪心算法的基本思路是从问题的某一个初始解出发一步一步地进行,根据某个优化测度,每一步都要确保能获得局部最优解。每一步只考虑一个数据,他的选取应该满足局部优化的条件。若下一个数据和部分最优解连在一起不再是可行解时,就不把该数据添加到部分解中,直到把所有数据枚举完,或者不能再添加算法停止 。
步骤
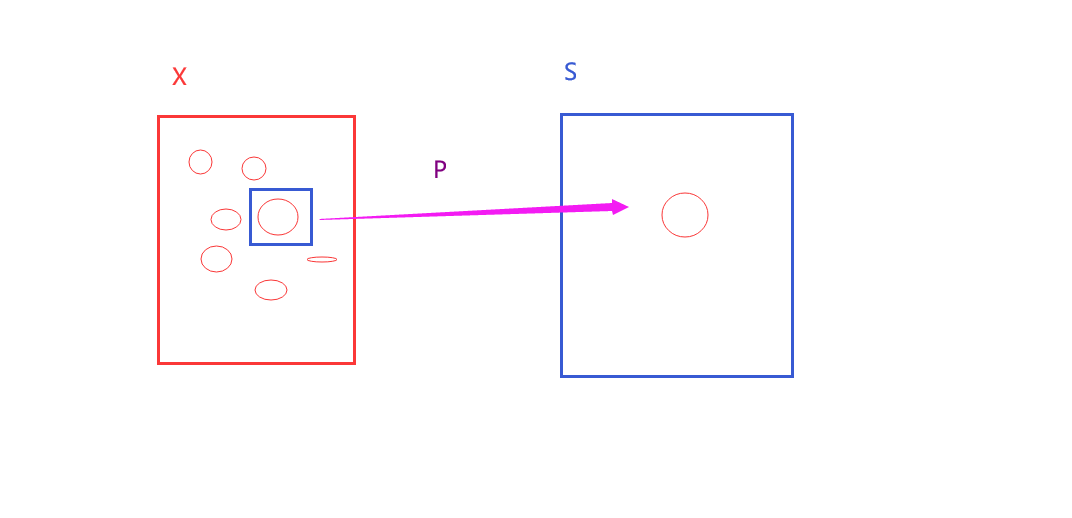
P即为贪心策略,用来选择符合条件的元素。
例子——硬币找零
假设某国硬币面值有1,5,10,25,100元五种面额,若店员为顾客找零时,需要给顾客找零a=36元,求硬币数最少的情况。

这里我们的贪心策略为:
先找到最接近a的值,然后对a进行更新,然后进行循环。
代码实现
def shortNum(a):
coins = [1,5,10,25,100]
out = []
coins = coins[::-1]
for i in coins:
num = a//i
out=out+[i,]*num
a = a-num*i
if a<=0:
break
return out
a = 36
print(shortNum(a))例子——任务规划
问题描述:
输入为任务集合X= [r1,r2,r3,...,rn],每个任务ri,都对应着一个起始时间ai与结束时间bi
要求输出为最多的相容的任务集。
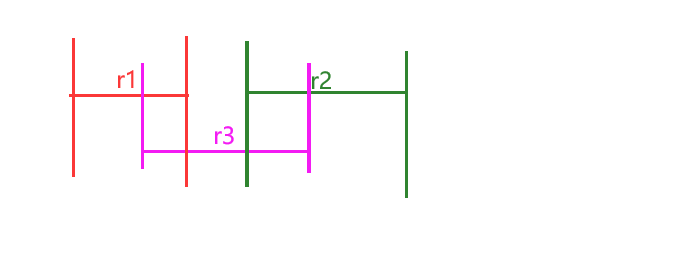
如上图,r1与r2相容,r3与r1和r2都不相容。
那么这里的贪心策略我们可以设为:
代码实现
# 任务规划
from collections import OrderedDict
task = OrderedDict()
task['r1'] = [0,4]
task['r2'] = [5,8]
task['r3'] = [10,13]
task['r4'] = [15,18]
task['r5'] = [7,11]
task['r6'] = [2,6]
task['r7'] = [2,6]
task['r8'] = [2,6]
task['r9'] = [12,16]
task['r10'] = [12,16]
task['r11'] = [12,16]
task['r12'] = [0,3]
listTask = list(task.items())
# 根据bi进行排序,结束时间早的在前面(冒泡排序)
for i in range(len(listTask)-1):
for j in range(len(listTask)-i-1):
if listTask[j][1][1] > listTask[j+1][1][1]:
listTask[j],listTask[j+1]=listTask[j+1],listTask[j]
print(listTask)
out = []
out.append(listTask.pop(0))
def isValid(temp,out):
for k in range(len(out)):
if temp[1][0]<out[k][1][1]:
# 相交
return False
return True
for j in range(len(listTask)):
temp = listTask.pop(0)
# 判断是否相交
# 相交则continue
# 不相交则out.append(temp)
for k in range(len(out)):
if isValid(temp,out):
out.append(temp)
# else:continue 语句可以不写
else:
continue
print(out)看完上述内容,你们掌握使用python 实现一个贪心算法的方法了吗?如果还想学到更多技能或想了解更多相关内容,欢迎关注亿速云行业资讯频道,感谢各位的阅读!
免责声明:本站发布的内容(图片、视频和文字)以原创、转载和分享为主,文章观点不代表本网站立场,如果涉及侵权请联系站长邮箱:is@yisu.com进行举报,并提供相关证据,一经查实,将立刻删除涉嫌侵权内容。