12函数执行过程_递归函数

目录

函数执行流程：... 1

recursion：... 3

recursion，递归函数

函数执行流程：

http://pythontutor.com/visualize.html#mode=edit

例：

def foo1(b,b1=3):

    print('foo1 called',b,b1)

def foo2(c):

    foo3(c)

    print('foo2 called',c)

def foo3(d):

    print('foo3 called',d)

def main():

    print('main called')

    foo1(100,101)

    foo2(200)

    print('main ending')

main()

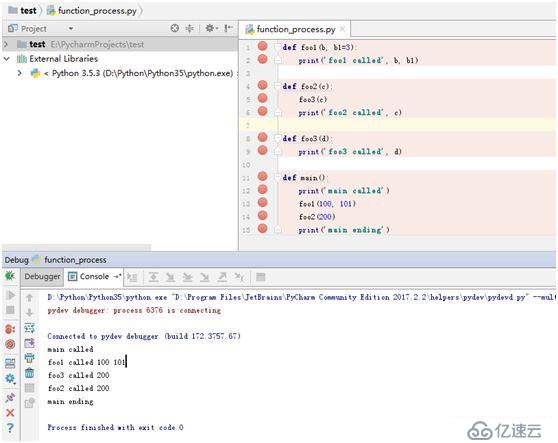
执行过程：

全局帧中生成foo1,foo2,foo3,main函数对象；

main函数调用；

main中查找内建函数print压栈，将常量字符串（main called）压栈，调用函数print，弹出栈顶；

main中全局查找函数foo1压栈，将常量100,101压栈，调用函数foo1，创建栈帧；print函数压栈，字符串和变量b,b1压栈，调用函数，弹出栈顶，返回值；

main中全局查找函数foo2压栈，将常量200压栈，调用函数foo2，创建栈帧；foo3函数压栈，变量c引用压栈，调用foo3，创建栈帧，foo3完成，print函数调用后返回；foo2恢复调用，执行print后返回值；

main中foo2调用结束，弹出栈顶；main继续执行，print函数调用，弹出栈顶，main函数返回；

注：

栈，后进先出；

保护当前函数运行的数据，出现函数调用，依次压栈；

保护现场-->函数压栈-->给函数创建空间frame-->在frame内执行-->依次出栈-->恢复现场；

recursion：

函数直接或者间接调用自身就是递归；

递归需要有边界条件、递归前进段（压栈）、递归返回段（弹出）；

递归一定要有边界条件（没有边界条件自己调自己会栈溢出、内存溢出，会将计算机资源耗尽，无限调用）；

当边界条件不满足时，递归前进；

当边界条件满足时，递归返回；

直接递归，自己调自己；

间接递归，通过别的函数调用了函数自身；

recursion要求：

一定要有退出条件，递归调用一定要执行到这个退出条件，没有退出条件的递归调用，就是无限调用；

递归调用的深度不宜过深，python对递归调用的深度作了限制，以保护解释器；超过递归深度限制，抛RecursionError: maximum recursion depth excedded超出最大深度；sys.getrecursionlimit()，总共不能超过1000层，自己可用980多，还有其它函数在用；sys.setrecursionlimit(2000)，不要改此项，生产中函数复杂，变量、常量各种对象都用内存；

recursion的性能：

循环稍微复杂一些，但只要不是死循环，可以多次迭代直至算出结果；

fib函数代码极简易懂，但只能获取到最外层的函数调用，内部递归结果都是中间结果，且给定一个n都要进行近2n次递归，深度越深效率越低，为了获取fibnacci需要外面再套一个n次的for循环，效率就更低了；

递归还有深度限制，如果递归复杂，函数反复压栈，堆内存很快就溢出了；

recursion总结：

递归是一种很自然的表达，符合逻辑思维；

递归相对运行效率低，每一次调用函数都要开辟栈帧；

递归有深度限制，如果递归层次太深，函数反复压栈，栈内存很快就溢出了；

如果是有限次数的递归，可以使用递归调用，或者使用循环代替，循环的代码稍复杂些，但只要不是死循环，可以多次迭代，直至算出结果；

绝大多数递归，都可使用循环实现；

即使递归代码很简洁，但能不用则不用；

fibnacci number

如果设F(n)为该数列的第n项，n∈N*，即F(n)=F(n-1)+F(n-2)；

F(0)=0

F(1)=1

F(n)=F(n-1)+F(n-2)

例：

import datetime
import sys

 start = datetime.datetime.now()
 pre = 0
cur = 1
print(pre,cur,end=' ')
 n = 35

for _ in range(n-1):
     pre,cur = cur,pre+cur
     print(cur,end=' ')
print()

 delta = (datetime.datetime.now() - start).total_seconds()
print(delta)

print(sys.getrecursionlimit())

例：

import datetime

 start = datetime.datetime.now()
def fib(n):
     return 1 if n < 2 else fib(n-1) + fib(n-2)

for i in range(35):
     print(fib(i),end=' ')
print()

 delta = (datetime.datetime.now() - start).total_seconds()
print(delta)

注：

代码虽很精简，但效率低，经测耗时8.127465s；

例：

def fib(n,pre=0,cur=1):
     pre,cur = cur,pre+cur
     print(cur,end=' ')
     if n == 2:
         return
     fib(n-1,pre,cur)

 fib(10)

注：

改进，与循环思想类似；

参数n是边界条件，用n来计数；

上一次的计算结果，直接作为函数的实参；

效率很高；

和循环比较，性能相近，所以递归并不一定效率低下，但递归有深度限制；

间接递归：

通过别的函数调用了函数自身，如果构成了循环递归调用是非常危险的，但是往往这种情况在代码复杂的情况下，还是可能发生这种调用，要用代码的规范（少用递归，脑跟）来避免这种递归调用的发生；

def foo1():

    foo2()

def foo2():

    foo1()

foo1()

习题：

1、求n的阶乘？

2、将一个数逆序放入列表中，1234-->[4,3,2,1]？

3、解决猴子吃桃问题？

1、

方一：

def fac(n):
     return 1 if n == 1 else n * fac(n-1)

print(fac(5))

方二：

def fac(num,mul=1):
     mul *= num
     if num == 1:
         return mul
     return fac(num-1,mul)

print(fac(5))

################

def fac(num,mul=None):
     if mul is None:
         mul = [1]
     if num == 1:
         return mul[0]
     mul[0] *= num
     fac(num-1,mul)
     return mul

print(fac(5))

################

def fac(num,mul=1):
     if num == 1:
         return mul
     mul *= num
     print(mul)
     fac(num-1,mul)
     return mul

 fac(5)

2、

方一：

def rev(num,lst=None):
     if lst is None:
         lst = []
     x,y = divmod(num,10)
     lst.append(y)
     if x == 0:
         return lst
     return rev(x,lst)

print(rev(1234))

方二：

def rev(num,target=[]):
     if num:
         target.append(num[len(num)-1])   #等价于target.append(num[-1:]
         rev(num[:len(num)-1])
     return target

print(rev(str(1234)))

注：

target是位置参数，只不过有默认值；rev(num,*,target),这个target是关键字参数且是keyword-only参数；位置参数的默认值放在__defaults__里，关键字参数的默认值在__kwdefaults__里；

函数对象没变，每次都是rev这个对象，所以该对象的默认值是固定的；

方三：

num = str(1234)

def rev(x):
     if x == -1:
         return ''
     return num[x] + rev(x-1)

print(rev(len(num)-1))

3、

def peach(days=10):
     if days == 1:
         return 1
     return (peach(days-1)+1) * 2

print(peach())

注：

这里必须是10，因为return (peach(days-1)+1)*2立即拿不到结果，必须通过再次进入函数时，判断是不是到了最后一天；即，当前使用的值是由下一次函数调用得到，所以要执行10次函数调用；

###############

def peach(days=1):   #days只用于计数
     if days == 10:
         return 1
     return (peach(days+1)+1) * 2

print(peach())