怎么用Python解决数据密度过大难题

本篇内容介绍了“怎么用Python解决数据密度过大难题”的有关知识，在实际案例的操作过程中，不少人都会遇到这样的困境，接下来就让小编带领大家学习一下如何处理这些情况吧！希望大家仔细阅读，能够学有所成！

什么是密度图?

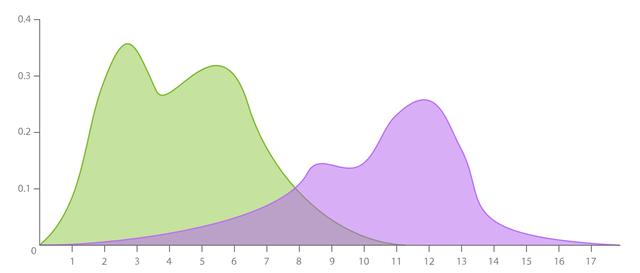
所谓的密度图 (Density Plot)  就是数据的分布稠密情况，它常用于显示数据在连续时间段内的分布状况。严格来说，它是由直方图演变而来，类似于把直方图进行了填充。

一般是使用平滑曲线来绘制数值水平来观察分布，峰值数值位置是该时间段内最高度集中的地方。

它比直方图适用性更强，不受分组数量(直方图的条形数量不宜过多)的影响，能更好地界定分布形状 。

本篇文章不谈论直方图，之后老海会专门总结关于直方图的使用。

什么是2D密度图?

说完了密度图和直方图，它们都是一维数据变量。

这下我们来看看2D密度图，它显示了数据集中两个定量变量范围内值的分布，有助于避免在散点图中过度绘制。

如果点太多，则2D密度图会计算2D空间特定区域内的观察次数。

该特定区域可以是正方形或六边形(六边形)，还可以估算2D内核密度估算值，并用轮廓表示它。

本篇文章主要描述一下2D密度图的使用。

2D密度图的基本数据样式

2D密度图的使用建议

• 密度图是一种直方图的代替方案，常用来观察连续变量的分布情况

• 2D密度图主要用来解决数据点密度过大的问题，要注意密度分割是否合理。

• 当数据范围都非常集中，数据间变化不大时，密度图往往很难观察效果。

下面开始具体的操作案例

准备工作

还是和之前一样，引入必要的工具包

## 初始字体设置，设置好可避免很多麻烦 plt.rcParams['font.sans-serif']=['Source Han Sans CN']      # 显示中文不乱码，思源黑体  plt.rcParams['font.size'] = 22                              # 设置图表全局字体大小，后期某个元素的字体大小可以自行调整 plt.rcParams['axes.unicode_minus'] = False                  # 显示负数不乱码 ## 初始化图表大小 plt.rcParams['figure.figsize'] = (20.0, 8.0)                # 设置figure_size尺寸 ## 初始化图表分辨率质量 plt.rcParams['savefig.dpi'] = 300                           # 设置图表保存时的像素分辨率 plt.rcParams['figure.dpi'] = 300                            # 设置图表绘制时的像素分辨率  ## 图表的颜色自定义 colors = ['#dc2624', '#2b4750', '#45a0a2', '#e87a59',          '#7dcaa9', '#649E7D', '#dc8018', '#C89F91',           '#6c6d6c', '#4f6268', '#c7cccf'] plt.rcParams['axes.prop_cycle'] = plt.cycler( color=colors)  path = 'D:\\系列文章\\' # 自定义文件路径，可以自行设定 os.chdir(path) # 设置为该路径为工作路径，一般存放数据源文件

设定图表样式和文件路径

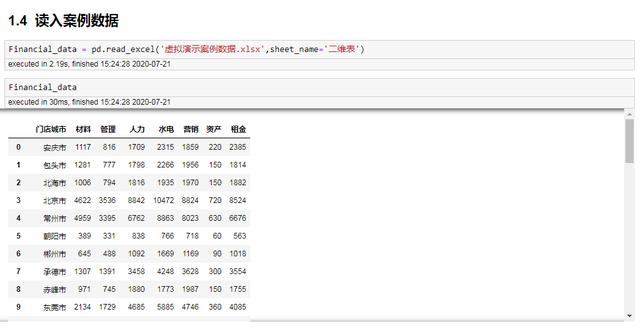
Financial_data = pd.read_excel('虚拟演示案例数据.xlsx',sheet_name='二维表') Financial_data

读入数据

Financial_data = pd.read_excel('虚拟演示案例数据.xlsx',sheet_name='二维表') Financial_data

常见的6种密度图表类型

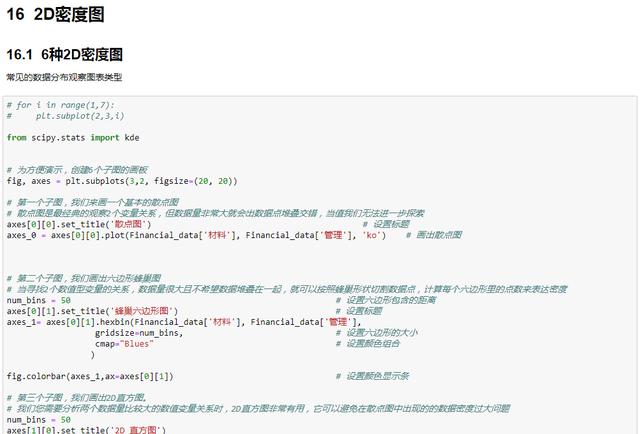
from scipy.stats import kde  # 引入核密度计算方法   # 为方便演示，创建6个子图的画板 fig, axes = plt.subplots(3,2, figsize=(20, 20))  # 第一个子图，我们来画一个基本的散点图 # 散点图是最经典的观察2个变量关系，但数据量非常大就会出数据点堆叠交错，当值我们无法进一步探索 axes[0][0].set_title('散点图')                                           # 设置标题 axes_0 = axes[0][0].plot(Financial_data['材料'], Financial_data['管理'], 'ko')    # 画出散点图    # 第二个子图，我们画出六边形蜂巢图 # 当寻找2个数值型变量的关系，数据量很大且不希望数据堆叠在一起，就可以按照蜂巢形状切割数据点，计算每个六边形里的点数来表达密度 num_bins = 50                                                      # 设置六边形包含的距离 axes[0][1].set_title('蜂巢六边形图')                                # 设置标题 axes_1= axes[0][1].hexbin(Financial_data['材料'], Financial_data['管理'],                    gridsize=num_bins,                               # 设置六边形的大小                   cmap="Blues"                                     # 设置颜色组合                  )  fig.colorbar(axes_1,ax=axes[0][1])                                 # 设置颜色显示条  # 第三个子图，我们画出2D直方图。 # 我们您需要分析两个数据量比较大的数值变量关系时，2D直方图非常有用，它可以避免在散点图中出现的的数据密度过大问题 num_bins = 50 axes[1][0].set_title('2D 直方图') axes_2 = axes[1][0].hist2d(Financial_data['材料'], Financial_data['管理'],                    bins=(num_bins,num_bins),                    cmap="Blues")  # fig.colorbar(axes_2,ax=axes[1][0])    # 第四个子图，我们画出高斯核密度图 # 考虑到想研究具有很多点的两个数值变量之间的关系。可以考虑绘图区域每个部分上的点数，来计算2D内核密度估计值。 # 就像平滑的直方图，这个方法不会使某个点掉入特定的容器中，而是会增加周围容器的权重，比如颜色会加深。 k = kde.gaussian_kde(Financial_data.loc[:,['材料','管理']].values.T)           # 进行核密度计算 xi, yi = np.mgrid[Financial_data['材料'].min():Financial_data['材料'].max():num_bins*1j, Financial_data['管理'].min():Financial_data['管理'].max():num_bins*1j] zi = k(np.vstack([xi.flatten(), yi.flatten()]))  axes[1][1].set_title('高斯核密度图') axes_3 = axes[1][1].pcolormesh(xi,                        yi,                        zi.reshape(xi.shape),                        cmap="Blues")  fig.colorbar(axes_3,ax=axes[1][1])                                  # 设置颜色显示条  # 第五个子图，我们画出带阴影效果的2D密度图 axes[2][0].set_title('带阴影效果的2D密度图') axes[2][0].pcolormesh(xi,                        yi,                        zi.reshape(xi.shape),                        shading='gouraud',                        cmap="Blues")   # 第六个子图，我们画出带轮廓线的密度图 axes[2][1].set_title('带阴影+轮廓线的2D密度图') axes_5 = axes[2][1].pcolormesh(xi,                        yi,                        zi.reshape(xi.shape),                        shading='gouraud',                        cmap="Blues")  fig.colorbar(axes_5,ax=axes[2][1])                                  # 设置颜色显示条  # 画出轮廓线 axes[2][1].contour(xi,                     yi,                     zi.reshape(xi.shape))  plt.show()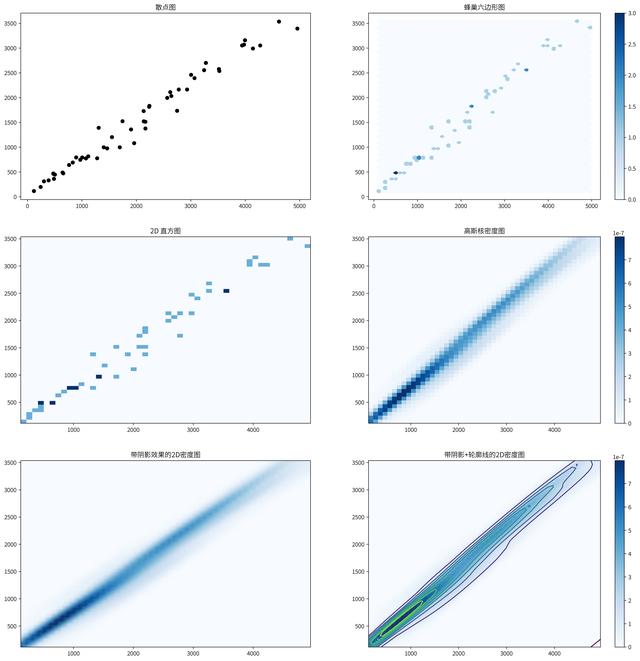

特别提一下：2D核密度估计图

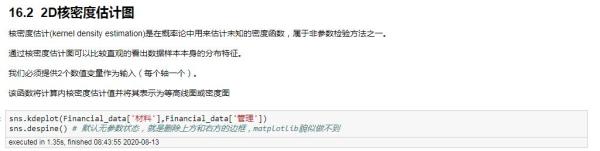
sns.kdeplot(Financial_data['材料'],Financial_data['管理']) sns.despine() # 默认无参数状态，就是删除上方和右方的边框，matplotlib貌似做不到

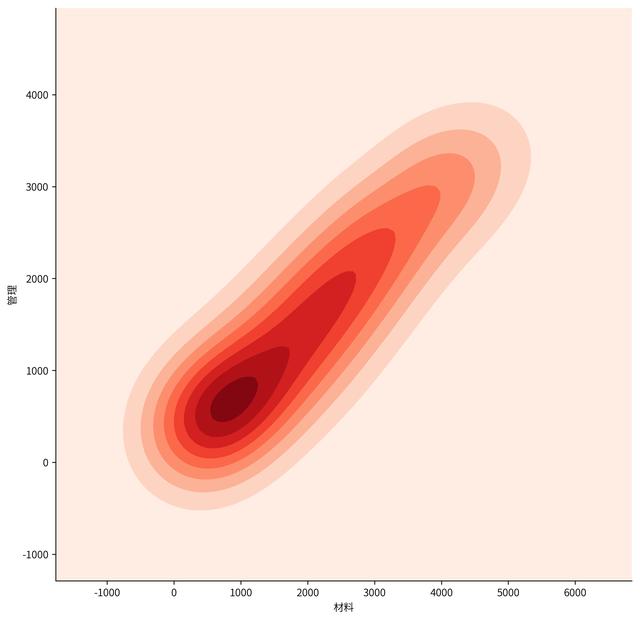
sns.kdeplot(Financial_data['材料'],Financial_data['管理'],             cmap="Reds",              shade=True,                                    # 若为True，则在kde曲线下面的区域中进行阴影处理，color控制曲线及阴影的颜色             shade_lowest=True,                        # 如果为True，则屏蔽双变量KDE图的最低轮廓。 #             bw=.15            ) sns.despine() # 默认无参数状态，就是删除上方和右方的边框，matplotlib貌似做不到

“怎么用Python解决数据密度过大难题”的内容就介绍到这里了，感谢大家的阅读。如果想了解更多行业相关的知识可以关注亿速云网站，小编将为大家输出更多高质量的实用文章！