大数据之数学类知识基础

数学相关的知识：

• 集合
• 函数极限，导数，微分，偏导数
• 向量
• 正弦余弦定理
• 最小二乘法
• 矩阵，正交矩阵

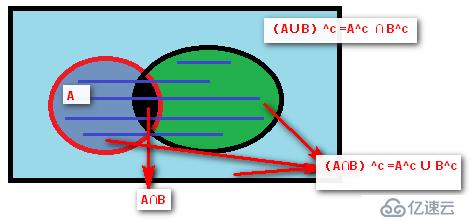
• 集合：是指具有某种特定性质的事物的总体，组成集合的事物称为元素。
   通常使用大写表示集合，小写表示元素；列举法，描述法
   列举法：A={a1,a2,a3,...,an},a1∈A
   描述法：B={x|x^2-1=0}，{x|x具有的性质}，方程的解即是组成B集合元素

  • 集合性质：
     A,B 若A的元素都是B集合的元素，则称A（B，A包含于B，若A=B，则表示集合AB相等；若A≠B，则A是B的真子集，A∈/≠B。
    交并补：
     A∩B、 A∪B、 A^c补集
    

• 函数
  奇偶函数：f(-x)=-f(x),f(x)=f(-x)
  初等函数：

  幂函数：y=X^u u∈常数
  指数函数：y=a^x;(a>0且a≠0)
  对数函数：y=logaX (a>0且a≠0,a=e时y=ln x)
  三角函数：y=sin x ,y=cos x,y=tan x
  反三角函数：y=arcsin x,y=arccos x,y=arctan x

• 闭区间连续函数的性质

  • 有界性与最大值和最小值定理
    区间I上有定义的f(x),x0∈I，使得对于任一x∈I，都有f(x)≤f(x0),f(x0)≥f(x),即f(x0)是f(x)在区间I上的最大值和最小值。

  • 零点定理
    如果x0使得f(x0)=0，则x0称为f(x)的零点
    设函数f(x)在闭区间【a,b】上连续，且f(a)与f(b)异号，即f(a)*f(b)<0，那么在开区间(a,b)内至少有一点e,使得f(e)=0
• 极限 ：割圆术
  概念：设{Xn}为一数列，如果存在常数a，对于任意给定的正数E（不论多么小），总存在正整数N，使得当n>N 时，不等式|Xn-a|<E，都成立，那么称a是数列的极限：lim Xn =a,n->∞
  • 函数极限
    0<|x-x0|<s, |f(X)-A|<E,当x->x0时；f(x)->A

• 导数
  切线问题,在曲线上取一点M(x0,y0)，当在曲线取另外一点N任意变化，但直线与曲线线切时，即相交于一点，|MN|->0,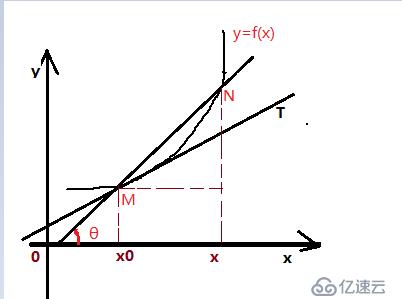
  
  MN直线的斜率：tanθ=（y-y0）/（x-x0）=[f(x)-f(x0)]/(x-x0)
  既有但x->x0时此时直线与曲线线切

  • 导数定义：
    有上述斜率可以归结为极限：lim [f(x)-f(x0)]/(x-x0) ,x->x0。
    定义：设函数y=f(x)，在点x0的某个领域内有定义，当自变量x在x0处取得增量△x(x0+△x在领域内)，则△y=f(x0+△x)-f(x0),当△x->0(即x->x0)时极限存在，则称函数在x0处可导，称这个极限为函数的导数记为：f `(x0).

   f `(x0)=lim(△y/△x)=lim [ f(x0+△x) - f(x0)] / △x
   也可记作：y*|x=x0 ,dy/dx |x=x0
  导数几何意义：切线的斜率

  • 常用初等函数导数

    1.(C)'=0   
    2.(x^u)'=ux^(u-1)
    3.(sinx)'=cosx
    4.(cosx)'=-sinx
    5.(tanx)'=sec^2 x
    6.(cotx)'=-csc^2 x
    7.(a^x)'=a^x *lna
    8.(e^x)'=e^x
    9.(logaX)'=1/(x*lna)
    10.(lnx)'=1/x
    11.(1/x)'=1/(x^2)

  • 求导法则：复合函数求导
    [ u(x) ± v(x) ] ' =u'(x) ± v'(x)
    [ u(x)·v(x) ] ' =u'(x)v(x) + u(x)v'(x)
    [ u(x) / v(x) ] '= [ u'(x)v(x) - u(x)v'(x) ] / v^2(x)
    dy/dx=(dy/du)*(du/dx)

  • 函数的微分与导数关系
    dy = f '(x)*dx

• 微分定义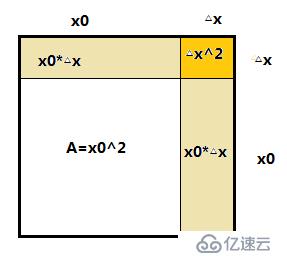
  
  设此薄片的边长为x0，面积为A，由于薄片受温度变化的影响时面积发生改变，对应长度增加△x,此时面积对应增加△A
  △A=（x0+△x）^2 - x0^2=2x0△x + (△x)^2
  ==>一般的：△y=A△x + 0(△x)--->替代(△x)^2即(△x)很小时，
  当△x高阶无穷小时A≠0，△y=A△x
  函数表示为：△y=f(x0+△x) - f(x0)=A△x + 0(△x)，称函数y=f(x)在点x0是可微的，而A△x叫做函数在点x0相应于自变量△x的微分，记作dy ,dy=A△x
  当△x-->0时；△y/△x=A+ o(△x)/△x ==>A=lim (△y/△x)=f '(x0)由此可见函数f(x)在x0处可微的充分必要条件是函数在点x0处可导：dy=f '(x0)△x-->dy=f '(x)dx

  • 微分几何意义，可以使用切线代替曲线段，线性代替非线性，近似计算，误差估计
  • 微分定理
    
  • 费马引理，即上述连续区间性质最大最小值定义使得：f(x)≤f(x0),f(x0)≥f(x)，那么f '(x)=0；可以通过f(x)在x0处可导条件及极限的保号性证明。通常称导数等于0的点为函数的驻点或者临界点
  • 罗尔定理：
    如果函数f(x)满足在区间【a,b】上连续；在开区间可导，在端点处函数f(a)=f(b)则在区间内至少有一点e使得f '(e)=0
• 函数的单调性与极值判定 (由以上定理求出函数的驻点来判断极大极小)
  • 单调性判断
    设函数y=f(x)在[a.b]上连续，在（a,b）上可导：
     如果f '(x)>0，那么y=f(x)在区间上单调递增
     如果f '(x)<0，那么y=f(x)在区间上单调递减
    
  • 极值判断
    利用二阶导数来判断图形的凹凸形结合单调性来得驻点是否是极值。
    设函数y=f(x)在[a.b]上连续，在（a,b）上具有一阶二阶可导：
     如果f ''(x)>0，那么y=f(x)在区间上图形是凹===>极小值
     如果f ''(x)<0，那么y=f(x)在区间上图形是凸===>极大值
    若二阶导数为0.直接由单调性判断大小，若f ''(x)≠0，则可以通过二阶导数判断大小，如上
    注：最值问题：f(x)在开区间（a,b）内除了有限个点外可导，且至多有有限个驻点，以及不可导点，极值可能是驻点或者不可导点。

• 偏导数
   研究一元函数时，我们从研究函数变化率引入了导数概念，对于多元函数同样研究它的变化率，但多元函数的自变量不止一个，因变量与自变量比一元函数复杂多。这时自变量当个逐一考虑，另外的自变量当做常数考虑。这时的导数称为偏导数。与一元函数定义类似。
  
   对应一元的微分，多元引入全微分：dz=(∂z/∂x)·△x+(∂z/∂y)·△y :△x-->dx
   二元函数的极值问题，一般可以利用偏导数来解决，跟一元类似处理。

  • 定理1：设函数z=f(x,y)在点（x0,y0）处具有偏导数，点f(x0,y0)处有极值，则fx(x0,y0)=0,fy(x0,y0)=0；
     同理一阶偏导=0的解称为驻点，驻点不一定是极值。
  • 定理2：研究驻点是否是极值
    设函数z=f(x,y)在点（x0,y0）的某领域内连续且有一阶二阶连续偏导数，fx(x0,y0)=0,fy(x0,y0)=0，令二阶偏导数：fxx(x0,y0)=A,fxy(x0,y0)=B,fyy(x0,y0)=C,则函数在点（x0,y0）取得极值的条件：
     1.AC-B^2>0时具有极值，A<0,时有极大值，当A>0时有极小值
     2.AC-B^2<0时没有极值
     2.AC-B^2=0时可能有极值，需另外考虑

    多元函数与一元函数类似，我们可以利用函数的极值来求函数的最大值和最小值

  例如：某厂要用钢板做成一个体积为2立方米的有盖长方形水箱。问当长宽高各取什么样的尺寸才最省材料？
   设长x m,宽y m,高为2/(xy)
   A=2( xy+y2/(xy) +x2/(xy) ),(x>0,y>0)
   Ax=2(y-2/(x^2))=0,Ay=2(x-2/(y^2))=0==>x y的值

  • 上述求极值是限制在定义域内，并无其他条件，拉格朗日乘法加入了有条件极值。
    公式：L(x,y)=f(x,y)+rφ（x,y），条件φ（x,y）=0，可以推广到多元适用
    联立解方程：
     fx(x,y)+rφx（x,y）=0
     fy(x,y)+rφy（x,y）=0
     rφ（x,y）=0
    比如：改为加入条件表面积为a^2下，而体积为最大？
    φ（x，y，z）=2xy+2yz+2xz-a^2=0 ,v=xyz联解即可。
• 最小二乘法，线性回归预测 ：有上述极值的算法在实践中常用的方法
  一元线性方程根据偏差的平方和为最小的条件来选择常数的方法叫做最小二乘法
   例子：为了测定刀具的磨损速度，做了这样的实验：经过一定时间（如每隔一小时），测量一次刀具的厚度，得到这样的数据：

为了确定时间与刀具厚度的关系，描点法在直角坐标系观察数据：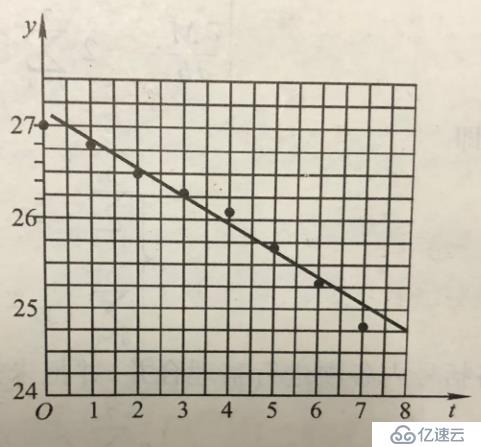

图中点大致接近于直线，线性负相关,可以设：f(t)=at+b,a,b常数
 因为这些点本来就不在一条直线上，那么只能要求函数在实验各点的取值尽量与实验的结果相差都很小，即要使各点误差最小:▲=yi-f(ti) (i=0,1,2,...7)
是否可以通过偏差求和来保证每个偏差最小：∑[yi-f(ti)] (i=0,1,2,...7) ？，从图中可以看出数据点分布在直线两侧，若通过求和方法，偏差有正负之分，会相互抵消。可通过取绝对值避免抵消偏差：∑ |yi-f(ti)]| (i=0,1,2,...7)，但不便于分析讨论。任何实数的平方都是正数或零：M=∑[yi-f(ti)]^2 (i=0,1,2,...7) 这种方法即最小二乘法。
 这时即求何时M取最小值，a,b为何值：由于yi,ti已知，把函数归结为M=M（a,b）求解,自变量看作a,b：上述的偏导数极值讨论：
 Ma(a,b)=0
 Mb(a,b)=0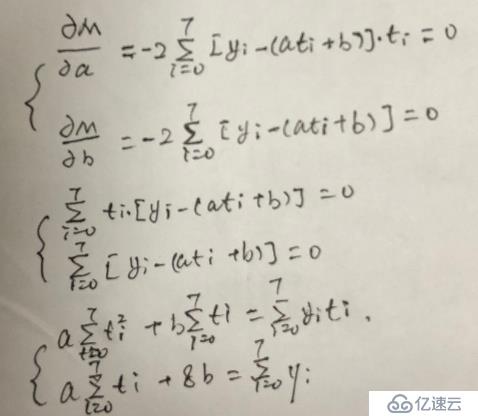

 此时计算出a,b相关项即可求出：y=at+b**

• 一元线性回归模型预测使用参数 的最小二乘估计，以上的通式是回归直线的解，可以看出回归直线通过(~x,~y)点，这也是重要特征之一。

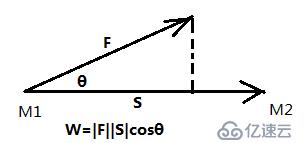
• 向量:既有大小又有方向（矢量）
  向量的大小叫做向量的模；注这里粗体表示向量,i, j, k空间直角坐标系单位向量
  向量线性运算：起点-->终点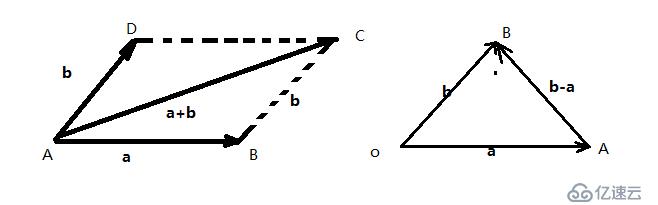
  
  a+b=AB+BC=c
  b+a=AD+DC=AC
  AB=AO+OB=OB-OA=b-a
  设a=(ax,ay,az) b=(bx,by.bz)==> a=axi+ayj+azk
  a+b等于对应坐标相加

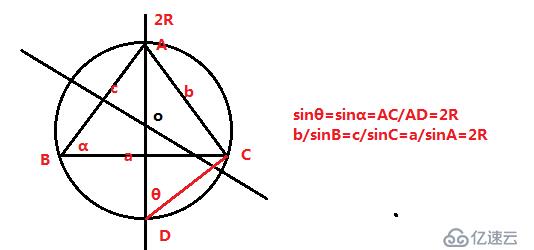
  • 向量的模-勾股定理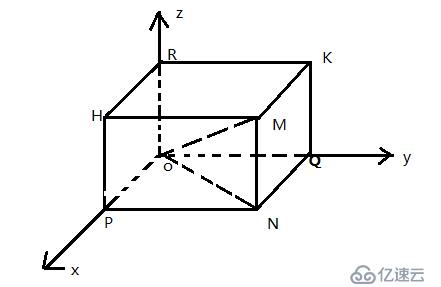
    
    设 r=(x,y,z)=OM ,OP=xi ,OQ=yi ,OR=zi
    OM=OP+OQ+OR
    |r|=|OM|=√[|OP|^2+|OQ|^2+|OR|^2 ]
    |r|=√x^2+y^2+z^2

  • 数量积
    
    物理做功问题，对个向量a和b做这样的运算结果为一个数，等于|a|、|b|及它们的夹角θ的余弦乘积称为这两个向量的数量积，记作a·b
     a·b=|a|×|b|cosθ
    坐标表示：a·b=axbx+ayby+azbz --对应坐标相乘相加
    注：向量积是一个向量：c=a×b，可以使用三阶行列式计算，点乘与×乘区别
• 正余弦定理：cosθ余弦相似性判断属性相似性
  正：任意三角形，各边和它所对的角的正弦值的比相等且等于外接圆的直径
   
  余：任意一边的平方等于其他两边平方和减去这两边与其夹角的余弦值两倍
  
  亦可以有上图：c=AB=b-a来证明，两边取平方，根据向量积定义得余弦定理

• 通信知识
  信号是消息的载体
  信息及其度量
   事件的不确定程度可以用其出现概率来描述。而消息中包含的信息量与消息发生的概率密切相关。消息出现的概率越小，则消息中包含的信息量就越大。假设p(x)表示消息发生的概率，I表示消息中的信息量，根据描述的关系：I=I[p(x)]
   p(x)越小，I越大，反之I越小；且当p(x)=1时，I=0，p(x)=0,I=∞
   I=loga [1/p(x)]=-loga[p(x)]
   信息量单位与a底数相关，a=2时，单位为比特bit；a=e时，单位为奈特nat；a=10时，单位为哈莱特Hartley.
   对于非等概率离散数据集；平均信息量表示又称为信息源的熵
   H(x)=p(x1)[-log2 p(x1)]+p(x2)[-log2 p(x2)]+.....+p(xm)[-log2 p(xm)]=-∑p(xi)*log2 p(xi)

• 对数运算
  性质：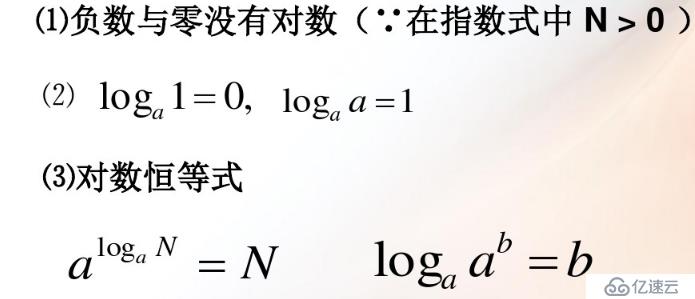
  

  对数的乘法性质：log(ab)=loga+logb
  对数的除法性质：log(a/b)=loga-logb
  对数的乘方性质：log(b^n)=(n/m)logb ，m为对数底的乘方
  换底公式：log(b)=log(b)/log(a)
  常用的有：log(b)=log(b)/log(a) (以10为底)
  log(b)=ln(b)/ln(a) (以e为底)

  linux中使用：

  log( x ) 返回 x 的自然对数e
  如求10的自然对数：
      awk 'BEGIN { fl=log(10); print fl }'
  如果求log(2,10),以2为底,10的对数：
      awk 'BEGIN { fl=(log(10)/log(2)); print fl }'
    #awk 'BEGIN{a=(log(4)/log(2));printf "%d\n" ,a/0.5}'

• 矩阵

  • 矩阵初等（行、列）变换
    对调两行
    以非零参数k乘以某一行全部元素，或再加到某一行上

  • 行列式运算

      主对角线-副对角线

  • n阶行列式的代数余子式

  高阶转换为低阶3--》2
  在三阶行列式中，将元素aij所在的第i行和第j列划去后，剩下的元素按元次序构成二阶行列式，称为aij的代数余子式，记为Mij，余子式前再冠之符号（-1）的（i+j）次方
  
  则三阶行列式的值等于该行列式的任意一行或一列的所有元元素与他们的代数余子式乘积之和。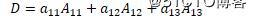
  

• 克拉默法则解线性方程
  高斯消元法，n个未知变量和方程如何求解
  注：克拉默法则只适用于未知数的个数与方程的个数相等的线性方程组，若不相等时不适用该法则。
  推论：

  如果齐次线性方程组有非零解，则其系数行列式D必须等于0.
  

• 特征值和特征向量