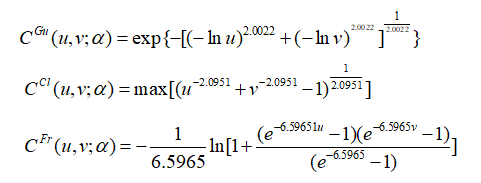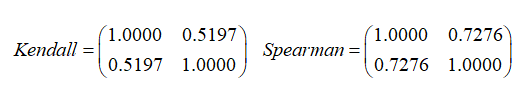今天就跟大家聊聊有关如何分析MATLAB中最优Copula函数的选择,可能很多人都不太了解,为了让大家更加了解,小编给大家总结了以下内容,希望大家根据这篇文章可以有所收获。
下面讲解Copula函数在实际生活中的应用,Copula函数描述的是变量间的相关性,实际上是一类将联合分布函数与它们各自的边缘分布函数连接在一起的函数,因此也有人将它称为连接函数。
Copula函数受到统计学者的青睐主要有以下两个原因:第一个是Copula是一种研究相依性测度的方法;第二个是Copula作为构造二维分布族的起点,可用于多元模型分布和随机模拟。
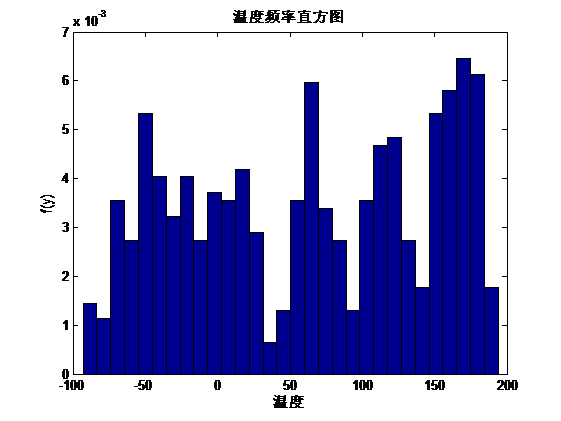
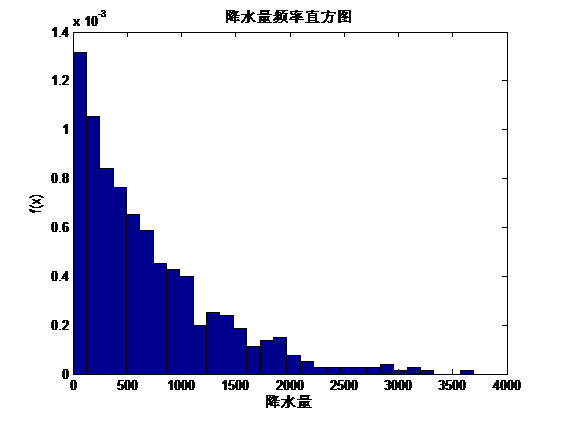
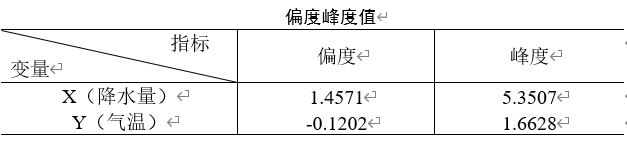
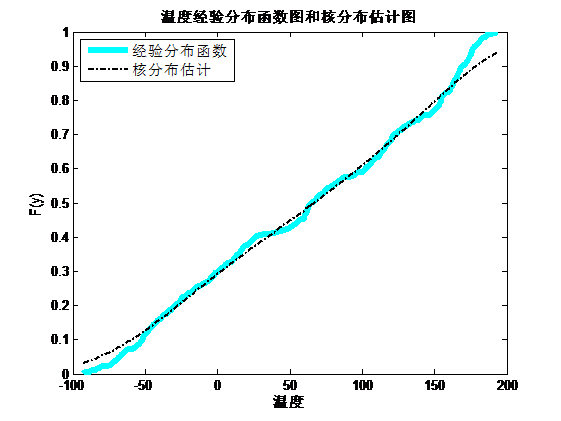
Copula函数作为一种变量之间相依机制的工具,几乎包含了随机变量所有的相依信息,在不能决定传统的线性相关系数能否正确度量变量之间的相关关系的情况下,Copula函数对变量之间相关关系的分析很有用,Copula函数的出现使变量之间的相依性刻画更加趋于完善。自从Copula方法被提出来后,Copula函数在金融资产收益率之间的相依性分析以及金融风险、金融风险管理等方面得到了广泛的应用。 在前期使用Copula熵法选择因子的分析中,从9个对降水有影响的因子中以降水量和气温为例,构造出降水量与气温的联合分布,比较各种类型Copula函数以选取最优的Copula函数。得到分析结果如下:本文首先以降水量和气温为两个随机变量记为X和Y,利用Matlab软件作出两个随机变量的频率直方图以及计算出二者的偏度和峰度,如下图所示:通过计算两个随机变量的峰度和偏度,以及作出二者的频率直方图并对频率直方图和偏度和峰度的分析,显然可以看出,二者的分布是不对称的,可以排除掉正态-Copula函数和t-Copula函数,为了进一步的分析以确定降水量和温度的分布类型,并筛选出合适的Copula函数,利用非参数法近似来估计总体的分布类型: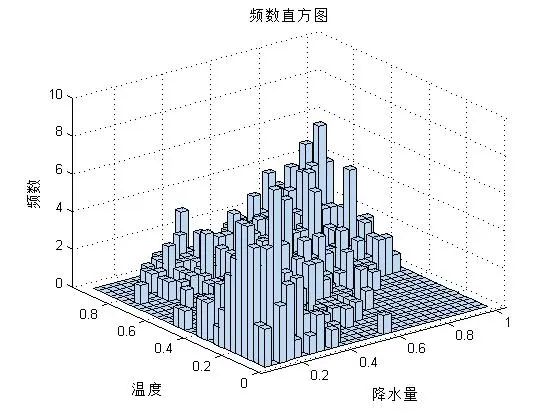
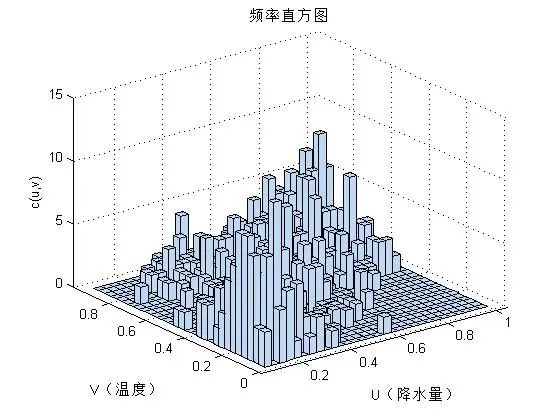
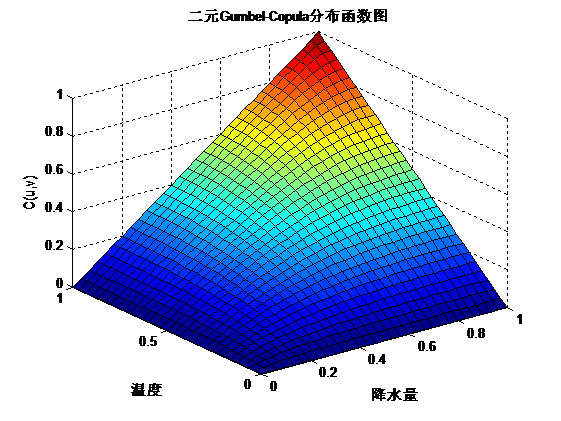
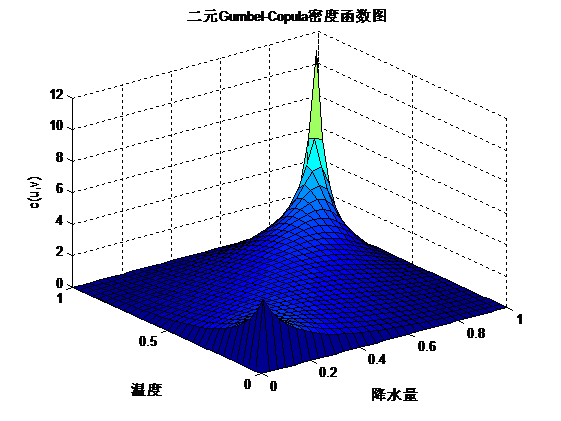
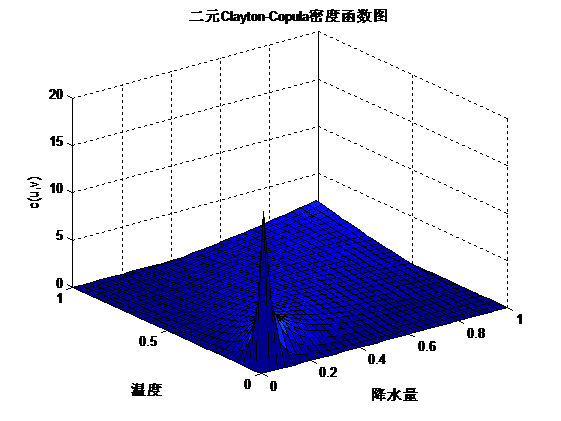
由上图可以确定经验分布函数和核分布函数以估计各自的边缘分布,通过分析二者频数和频率分布,可以清晰的看出来二者的尾部是不对称的,可选用阿基米德型-Copula函数来描述二者之间的关系。计算得出三者的参数值为:有此表达式,作出三种Copula函数的密度函数图和分布函数图如下所示:二元Gumbel-Copula密度函数和分布函数图
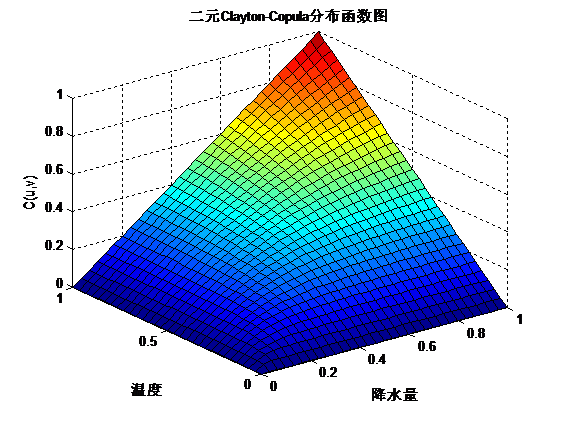
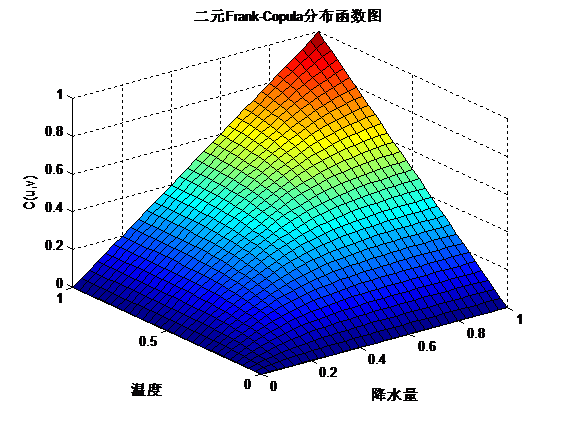
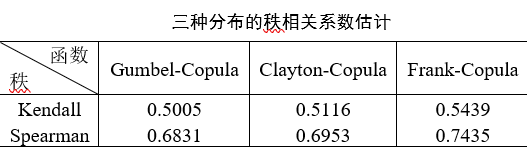
二元Clayton-Copula密度函数和分布函数图从密度函数图和分布函数图可以看出对于二元的Frank-Copula函数具有较厚的尾部,更能反应出二者之间的关系。通过计算得出该类型的Copula函数的尾部相关系数以及利用Copulastat函数计算三种函数的秩相关系数:利用Corr函数求出Kendall和Spearman秩相关系数为:
计算平方欧氏距离得出:对于Gumbel-Copula型函数距离为0.27;Clayton-Copula距离为0.1234;Frank-Copula距离为0.2159,在三者中,Clayton-Copula函数的平方欧式距离较小,在二者的联合分布中可选用Clayton-Copula函数,该函数可以更好的展现二者之间的关系。
看完上述内容,你们对如何分析MATLAB中最优Copula函数的选择有进一步的了解吗?如果还想了解更多知识或者相关内容,请关注亿速云行业资讯频道,感谢大家的支持。