构造CVRP问题初始解的启发式方法是什么呢

这篇文章给大家介绍构造CVRP问题初始解的启发式方法是什么呢，内容非常详细，感兴趣的小伙伴们可以参考借鉴，希望对大家能有所帮助。

一种构造CVRP问题初始解的启发式方法的matlab代码完成了，小编先帮大家回忆一下CW节约算法构造CVRP问题初始解的流程。

小编使用的是solomon算例中的c102算例，小编将所有的solomon算例与代码放在一起了，文末会给出链接。小编先解释一下横向各英文单词代表什么，CUST NO.=顾客序号；XCOORD.=X坐标；YCOORD. =Y坐标；DEMAND=需求量；READY TIME=顾客允许接收服务的最早时间；DUE DATE=顾客允许接收服务的最晚时间；SERVICE TIME=顾客所需的服务时间，其中READY TIM、DUE DATE和SERVICE TIME在求CVRP问题时用不上，这三个数在求解带时间窗的车辆路径问题（VRPTW）会派上用场，这里小编不再多说。

首先放出初始时配送中心和顾客的分布图，是这个样子的：

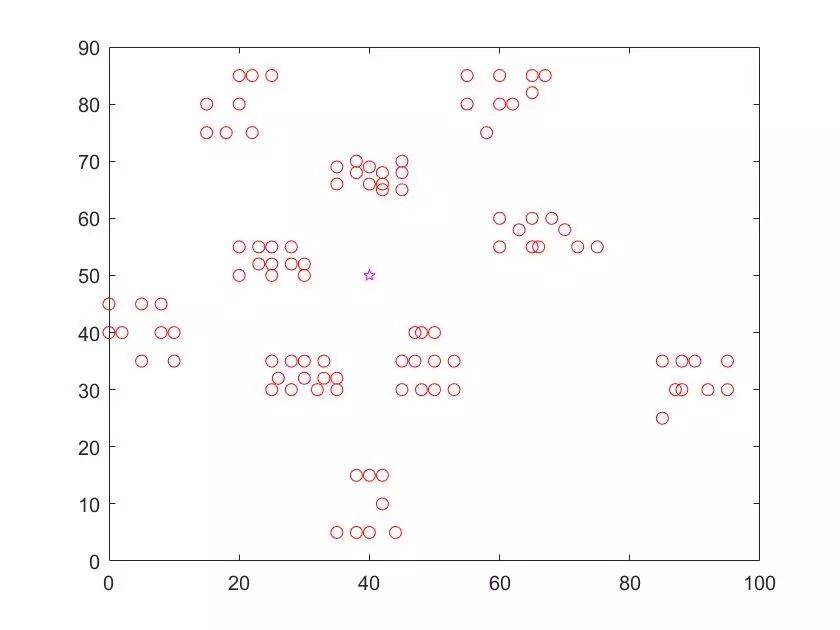
在使用节约算法构造初始解后，效果如下所示：

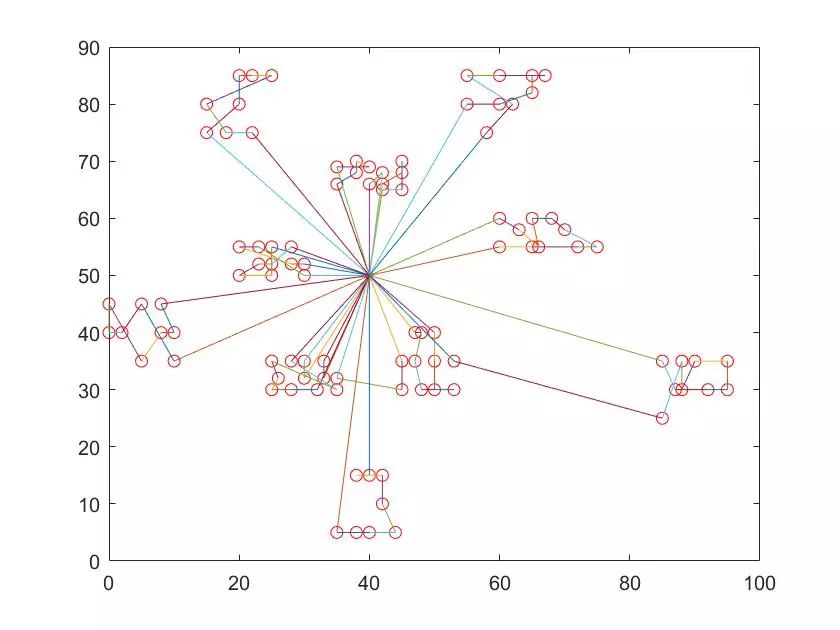
各个车辆所经过顾客序号如下所示，其中0代表配送中心，一共用了16辆车，初始解中所有车辆所行驶的总距离为1143.3

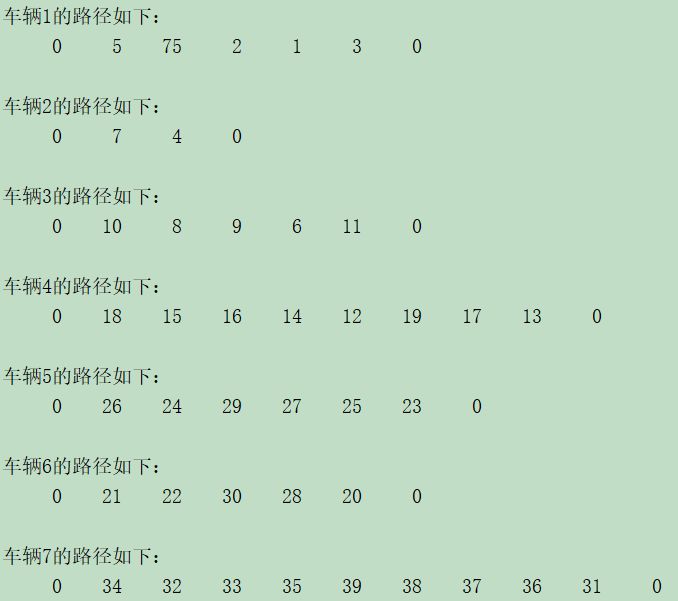
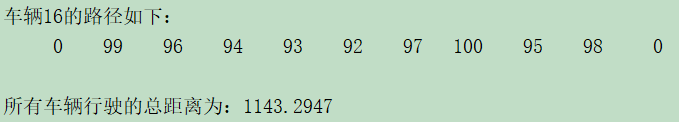
16辆车每辆车所运输货物的载重量都没超过容量限制，即没超过200（正好等于200，是可以允许的）

可能看到这里，各位小伙伴会注意到，有些车辆明显所经过的顾客的数量少，并且所运输的货物的重量远没达到200，很明显可以将这条路径融合到相应的路径上。在这里小编也注意到了，但是这个节约算法是构造CVRP问题的初始解，接下来的进一步优化还需要各位小伙伴努力完成啦。

关于构造CVRP问题初始解的启发式方法是什么呢就分享到这里了，希望以上内容可以对大家有一定的帮助，可以学到更多知识。如果觉得文章不错，可以把它分享出去让更多的人看到。