您好,登录后才能下订单哦!
这篇文章将为大家详细讲解有关数据结构之树的示例分析,文章内容质量较高,因此小编分享给大家做个参考,希望大家阅读完这篇文章后对相关知识有一定的了解。
一、树简介
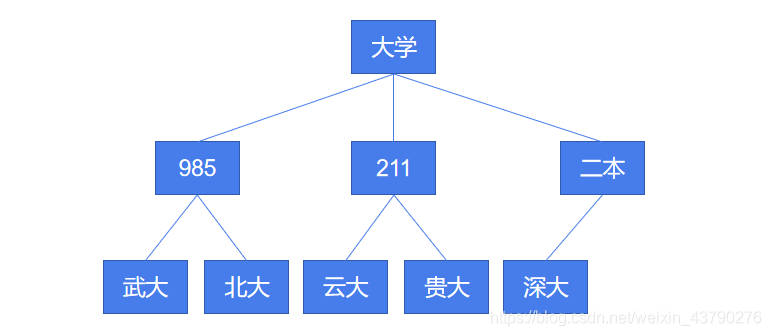
树(Tree)是一种抽象的数据结构,是一个数据的集合,集合中的数据组成了一个树状结构。例如上图,看起来像一棵倒挂的树,根朝上叶朝下。
树是由n(n>=0)个节点组成的具有层次关系的数据集合。当 n=0 时,树中没有节点,称为空树。当 n>0 时,有且仅有一个节点被称为根节点(Root),如果 n=1 ,树只有根节点一个节点。如果 n>1 ,除根节点外,将其余的节点分成m(m>0)个互不相交的数据集合,这 m 个集合每一个都要满足树的结构(有且仅有一个根节点),并且这 m 棵树都“挂”在根节点上,如此递归下去,直到所有节点都“挂”到这棵树上。其中,这 m 个集合构成的 m 棵树都被称为根节点的子树。
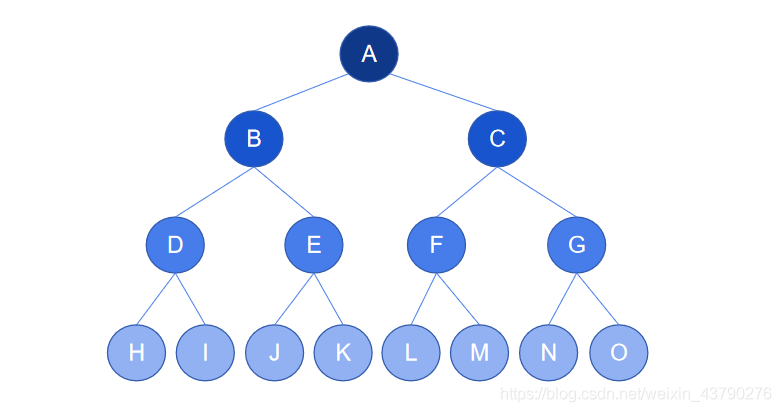
在理解树的结构和定义时,需要运用到递归的思想。以下图为例,树的节点集合为 {A,B,C,D,E,F,G,H} ,n=8,根节点为 A ,除根节点 A 外,其余节点组成了两个(m=2)集合(m1和m2),m1集合为 {B,D,E} ,m2集合为 {C,F,G,H} 。在m1中,B 为m1的根节点,除 B 以外,其余节点组成两个集合,集合 {D} 和集合 {E} ,{D} 和 {E} 都只有一个节点,分别构成一棵只有一个节点的树,它们“挂”在m1的根节点 B 上,是 B 的子树,m1构成一棵树,“挂”在根节点 A 上,m1是 A 的子树。同理,在m2中,C 为m2根节点,其余节点组成三个集合 {F} 、{G} 和 {H} ......
二、树的术语
要理解树这种数据结构,必须先理解一些常用的术语。
树由一个一个的节点组成,节点是构成复杂数据结构的基本组成单位。
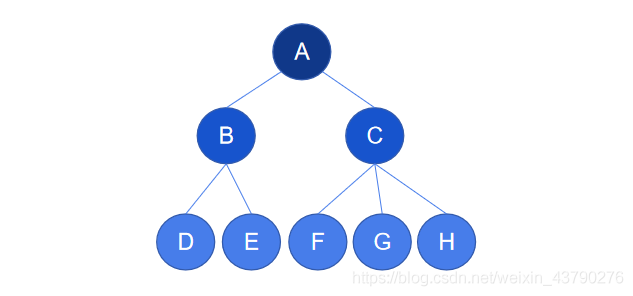
1. 子节点:又称为孩子节点,一个节点所包含的子树的根节点被称为该节点的子节点。如下图中,节点 B 有两棵子树,这两棵子树的根节点为 D 和 E ,所以 D 和 E 都是 B 的子节点。
2. 父节点:又称为父亲节点,如果一个节点有子节点,则这个节点被称为其子节点的父节点。如下图中,节点 B 有两个子节点 D 和 E ,则 B 是 D 的父节点,也是 E 的父节点。
3. 兄弟节点:具有相同父节点的节点互称为兄弟节点。下图中的 D 和 E 就互为兄弟节点。
4. 堂兄弟节点:如果树的两个节点深度相同,但父节点不同,则它们互为堂兄弟节点。下图中的 D与F,D与G,D与H,D与I 都是堂兄弟节点关系。
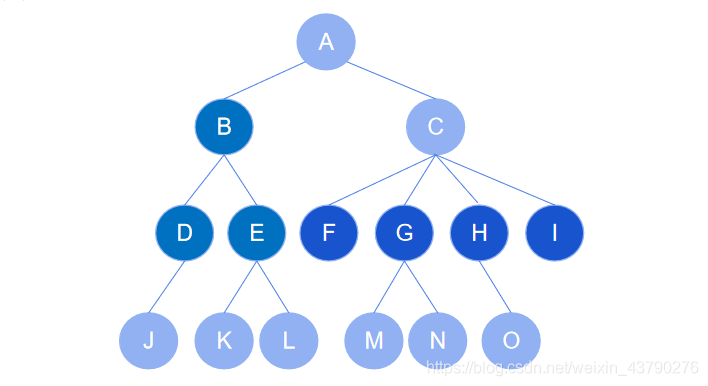
5. 节点的祖先:从根节点开始,依次找到某节点所经路径上的所有节点都称为该节点的祖先。如下图中,节点 J 的祖先节点为 A,B,D 。
6. 节点的子孙:以某节点为根的子树中,任一节点都称为该节点的子孙。如下图中,节点 C 的子孙有 F,G,H,I,M,N,O 。
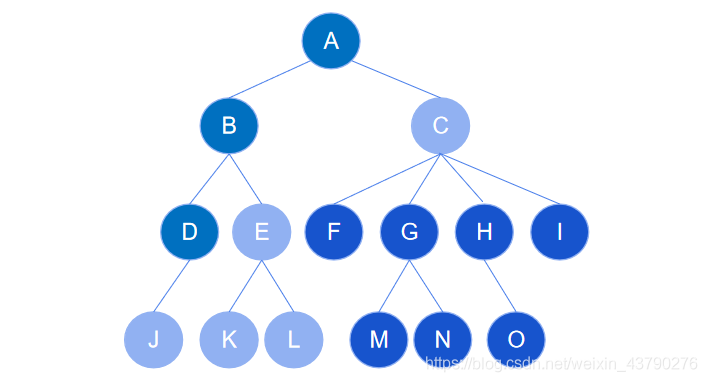
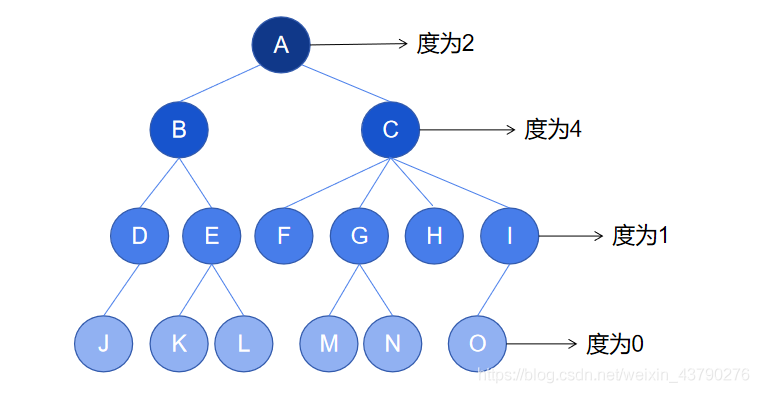
7. 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推。如下图中,根节点 A 在第1层,节点 M 在第4层。
8. 节点的深度:一个节点所处的层次称为该节点的深度。如下图中,根节点 A 的深度为1,节点 M 的深度为4 。(上面解释堂兄弟节点时有用到节点的深度,现在可以回去看看)
9. 树的深度:又称为树的高度,一棵树中,最大的节点深度称为树的深度。如下图中的树深度为4。
关于深度和高度,有两种定义方式,一种是将根节点的深度定义为0,另一种是将根节点的深度定义为1。但不管怎样,每个深度为 k 的节点的子节点的深度都为 k+1 ,这是不变的。
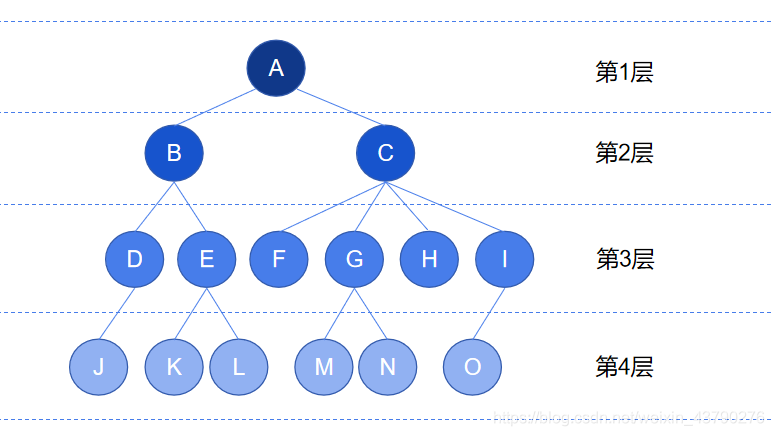
10. 节点的度:一个节点含有的子树(或子节点)的个数称为该节点的度。如下图中, 根节点 A 的度为2,节点 C 的度为4,节点 I 的度为1,节点 O 的度为 0 。
11. 树的度:一棵树中,最大的节点度称为树的度。如下图中,最大的节点度是4,则树的度为4。
12. 叶节点:又称为终端节点,度为零的节点被称为叶节点。如下图中,节点 F,H,J,K,L,M,N,O 都是叶节点。
13. 森林:由m(m>=0)棵互不相交的树构成的集合称为森林。森林是从树延伸出来的术语,森林里的树一定是互不相交的。
三、树的特点
通过对树的定义和树的术语进行介绍,基本可以理解树这种数据结构了,总结起来,树有以下特点。
1. 如果树的节点数 n>0,根节点是唯一的,不可能存在多个根节点。
2. 没有父节点的节点称为根节点。根节点是没有父节点的。
3. 每一个非根节点有且只有一个父节点。除了根节点外,其他所有节点都有父节点,并且同一个节点只有一个父节点,不可能有多个。
4. 每个节点有零个或多个子节点。
5. 除了根节点外,子节点可以分为多个不相交的子树。这些子树一定是互不相交的。
6. 每个深度为 k 的节点的子节点的深度都为 k+1 。
四、树的分类
所有树都满足以上的特点,除此之外,一些树还具有专有的特点。根据专有的特点,可以对树进行分类。
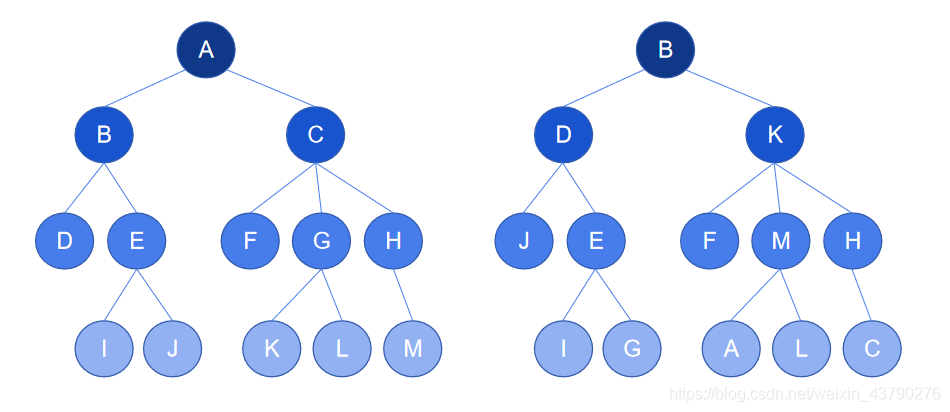
1. 无序树:也称为自由树,树中存在一个节点,节点的子节点之间没有顺序关系。如下图中,右边的树是无序树,从树中取一个节点 D ,D 的子节点是节点 J 和节点 E,它们是没有顺序关系的,所以这是一棵无序树。
2. 有序树:树中任意节点的子节点之间有顺序关系。如下图中,左边的树是有序树,从树中任意取一个节点 C,C 的子节点是 F,G,H ,它们是有顺序关系的(字母顺序),所以这是一棵有序树。
图中的有序和无序以字母顺序作为案例,实际应用中的“有序”并不限于字母顺序、数字顺序等,实际的有序主要是指“不能互换”。
无序树的节点之间没有顺序关系,节点之间的关系不能通过代码来模拟和控制,所以基本没有实际的应用场景。
使用树这种数据结构,基本都是使用有序树,对于有序树,又可以分为以下几种。
1. 二叉树:每个节点最多含有两个子树的树称为二叉树,如下图。二叉树是最常用的树结构,可以对二叉树进一步细分(另外的文章再仔细研究)。
2. 霍夫曼树:又称为最优二叉树,是一种带权路径最短的二叉树。
3. B树:是一种对读写操作进行优化的自平衡的二叉查找树,能够保持数据有序,拥有多余两个子树。
关于数据结构之树的示例分析就分享到这里了,希望以上内容可以对大家有一定的帮助,可以学到更多知识。如果觉得文章不错,可以把它分享出去让更多的人看到。
免责声明:本站发布的内容(图片、视频和文字)以原创、转载和分享为主,文章观点不代表本网站立场,如果涉及侵权请联系站长邮箱:is@yisu.com进行举报,并提供相关证据,一经查实,将立刻删除涉嫌侵权内容。