жӮЁеҘҪпјҢзҷ»еҪ•еҗҺжүҚиғҪдёӢи®ўеҚ•е“ҰпјҒ
иҝҷзҜҮж–Үз« дё»иҰҒдёәеӨ§е®¶еұ•зӨәдәҶвҖңеҰӮдҪ•дҪҝз”ЁPythonе’ҢMatlaе®һзҺ°жЁЎжӢҹйҖҖзҒ«жі•вҖқпјҢеҶ…е®№з®ҖиҖҢжҳ“жҮӮпјҢжқЎзҗҶжё…жҷ°пјҢеёҢжңӣиғҪеӨҹеё®еҠ©еӨ§е®¶и§ЈеҶіз–‘жғ‘пјҢдёӢйқўи®©е°Ҹзј–еёҰйўҶеӨ§е®¶дёҖиө·з ”究并еӯҰд№ дёҖдёӢвҖңеҰӮдҪ•дҪҝз”ЁPythonе’ҢMatlaе®һзҺ°жЁЎжӢҹйҖҖзҒ«жі•вҖқиҝҷзҜҮж–Үз« еҗ§гҖӮ
жҲ‘еңЁеүҚйқўе·Із»Ҹз»ҷеҮәдәҶжЁЎжӢҹйҖҖзҒ«жі•зҡ„е®Ңж•ҙзҹҘиҜҶзӮ№е’Ңжәҗз Ғе®һзҺ°пјҡжҷәиғҪдјҳеҢ–з®—жі•—иҡҒзҫӨз®—жі•пјҲPythonе®һзҺ°пјү
жЁЎжӢҹйҖҖзҒ«е’Ңи’ҷзү№еҚЎжҙӣе®һйӘҢдёҖж ·пјҢе…ЁеұҖйҡҸжңәпјҢз”ұдәҺжІЎжңүиҮӘйҖӮеә”зҡ„иҝҮзЁӢ(дҫӢеҰӮеҗ‘жңҖдјҳйқ иҝ‘гҖҒжқғйҮҚжўҜеәҰдёӢйҷҚзӯү)пјҢеҜ№дәҺеӨҚжқӮеҮҪж•°еҜ»дјҳпјҢеҫҲйҡҫдјҡжүҫеҲ°жңҖдјҳи§ЈпјҢйғҪжҳҜиҝ‘дјјжңҖдјҳи§Јпјӣ然иҖҢеғҸиқҷиқ з®—жі•гҖҒзІ’еӯҗзҫӨз®—жі•зӯүжңүеҗ‘жңҖдјҳйҖјиҝ‘дё”йҖҡиҝҮжңҖдјҳжңҖе·®и°ғж•ҙеҸӮж•°зҡ„жӯҘйӘӨпјҢиҷҪ然еҜ№дәҺдёӢеӣҫеҮҪж•°жҳ“йҷ·е…ҘеұҖйғЁжңҖдјҳпјҢдҪҶжҳҜеҜ»дјҳзІҫеәҰзӣёеҜ№иҫғй«ҳгҖӮеҰӮжһңзҗҶи§Јиҝҷж®өиҜқеә”иҜҘе°ұжҳҺзҷҪдәҶдёәд»Җд№ҲзҘһз»ҸзҪ‘з»ңи®ӯз»ғеүҚеҰӮжһңеҲқжӯҘеҜ»дјҳдёҖз»„иҫғеҘҪзҡ„зҪ‘з»ңеҸӮж•°пјҢдјҡдҪҝи®ӯз»ғж•ҲжһңжҸҗй«ҳеҫҲеӨҡпјҢд№ҹдјҡжӣҙеҝ«иҫҫеҲ°иҜҜе·®зІҫеәҰгҖӮ
#===========1еҜјеҢ…================
import matplotlib.pyplot as plt
import pandas as pd
from sko.SA import SA
#============2е®ҡд№үй—®йўҳ===============
fun = lambda x: x[0] ** 2 + (x[1] - 0.05) ** 2 + x[2] ** 2
#=========3иҝҗиЎҢжЁЎжӢҹйҖҖзҒ«з®—жі•===========
sa = SA(func=fun, x0=[1, 1, 1], T_max=1, T_min=1e-9, L=300, max_stay_counter=150)
best_x, best_y = sa.run()
print('best_x:', best_x, 'best_y', best_y)
#=======4з”»еҮәз»“жһң=======
plt.plot(pd.DataFrame(sa.best_y_history).cummin(axis=0))
plt.show()
#scikit-opt иҝҳжҸҗдҫӣдәҶдёүз§ҚжЁЎжӢҹйҖҖзҒ«жөҒжҙҫ: Fast, Boltzmann, Cauchy.
#===========1.1 Fast Simulated Annealing=====================
from sko.SA import SAFast
sa_fast = SAFast(func=demo_func, x0=[1, 1, 1], T_max=1, T_min=1e-9, q=0.99, L=300, max_stay_counter=150)
sa_fast.run()
print('Fast Simulated Annealing: best_x is ', sa_fast.best_x, 'best_y is ', sa_fast.best_y)
#===========1.2 Fast Simulated Annealing with bounds=====================
from sko.SA import SAFast
sa_fast = SAFast(func=demo_func, x0=[1, 1, 1], T_max=1, T_min=1e-9, q=0.99, L=300, max_stay_counter=150,
lb=[-1, 1, -1], ub=[2, 3, 4])
sa_fast.run()
print('Fast Simulated Annealing with bounds: best_x is ', sa_fast.best_x, 'best_y is ', sa_fast.best_y)
#===========2.1 Boltzmann Simulated Annealing====================
from sko.SA import SABoltzmann
sa_boltzmann = SABoltzmann(func=demo_func, x0=[1, 1, 1], T_max=1, T_min=1e-9, q=0.99, L=300, max_stay_counter=150)
sa_boltzmann.run()
print('Boltzmann Simulated Annealing: best_x is ', sa_boltzmann.best_x, 'best_y is ', sa_fast.best_y)
#===========2.2 Boltzmann Simulated Annealing with bounds====================
from sko.SA import SABoltzmann
sa_boltzmann = SABoltzmann(func=demo_func, x0=[1, 1, 1], T_max=1, T_min=1e-9, q=0.99, L=300, max_stay_counter=150,
lb=-1, ub=[2, 3, 4])
sa_boltzmann.run()
print('Boltzmann Simulated Annealing with bounds: best_x is ', sa_boltzmann.best_x, 'best_y is ', sa_fast.best_y)
#==================3.1 Cauchy Simulated Annealing==================
from sko.SA import SACauchy
sa_cauchy = SACauchy(func=demo_func, x0=[1, 1, 1], T_max=1, T_min=1e-9, q=0.99, L=300, max_stay_counter=150)
sa_cauchy.run()
print('Cauchy Simulated Annealing: best_x is ', sa_cauchy.best_x, 'best_y is ', sa_cauchy.best_y)
#==================3.2 Cauchy Simulated Annealing with bounds==================
from sko.SA import SACauchy
sa_cauchy = SACauchy(func=demo_func, x0=[1, 1, 1], T_max=1, T_min=1e-9, q=0.99, L=300, max_stay_counter=150,
lb=[-1, 1, -1], ub=[2, 3, 4])
sa_cauchy.run()
print('Cauchy Simulated Annealing with bounds: best_x is ', sa_cauchy.best_x, 'best_y is ', sa_cauchy.best_y)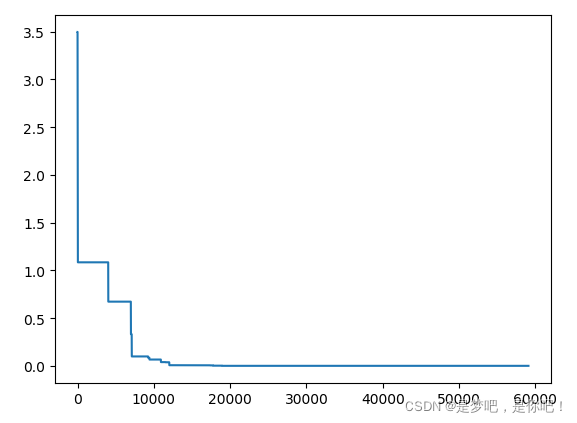
clear
clc
T=1000; %еҲқе§ӢеҢ–жё©еәҰеҖј
T_min=1; %и®ҫзҪ®жё©еәҰдёӢз•Ң
alpha=0.99; %жё©еәҰзҡ„дёӢйҷҚзҺҮ
num=1000; %йў—зІ’жҖ»ж•°
n=2; %иҮӘеҸҳйҮҸдёӘж•°
sub=[-5,-5]; %иҮӘеҸҳйҮҸдёӢйҷҗ
up=[5,5]; %иҮӘеҸҳйҮҸдёҠйҷҗ
tu
for i=1:num
for j=1:n
x(i,j)=(up(j)-sub(j))*rand+sub(j);
end
fx(i,1)=fun(x(i,1),x(i,2));
end
%д»ҘжңҖе°ҸеҢ–дёәдҫӢ
[bestf,a]=min(fx);
bestx=x(a,:);
trace(1)=bestf;
while(T>T_min)
for i=1:num
for j=1:n
xx(i,j)=(up(j)-sub(j))*rand+sub(j);
end
ff(i,1)=fun(xx(i,1),xx(i,2));
delta=ff(i,1)-fx(i,1);
if delta<0
fx(i,1)=ff(i,1);
x(i,:)=xx(i,:);
else
P=exp(-delta/T);
if P>rand
fx(i,1)=ff(i,1);
x(i,:)=xx(i,:);
end
end
end
if min(fx)<bestf
[bestf,a]=min(fx);
bestx=x(a,:);
end
trace=[trace;bestf];
T=T*alpha;
end
disp('жңҖдјҳи§Јдёәпјҡ')
disp(bestx)
disp('жңҖдјҳеҖјдёәпјҡ')
disp(bestf)
hold on
plot3(bestx(1),bestx(2),bestf,'ro','LineWidth',5)
figure
plot(trace)
xlabel('иҝӯд»Јж¬Ўж•°')
ylabel('еҮҪж•°еҖј')
title('жЁЎжӢҹйҖҖзҒ«з®—жі•')
legend('жңҖдјҳеҖј')function z=fun(x,y) z = x.^2 + y.^2 - 10*cos(2*pi*x) - 10*cos(2*pi*y) + 20;
function tu
[x,y] = meshgrid(-5:0.1:5,-5:0.1:5);
z = x.^2 + y.^2 - 10*cos(2*pi*x) - 10*cos(2*pi*y) + 20;
figure
mesh(x,y,z)%е»әдёҖдёӘзҪ‘ж јеӣҫпјҢиҜҘзҪ‘ж јеӣҫдёәдёүз»ҙжӣІйқўпјҢжңүе®һиүІиҫ№йўңиүІпјҢж— йқўйўңиүІ
hold on
xlabel('x')
ylabel('y')
zlabel('z')
title('z = x^2 + y^2 - 10*cos(2*pi*x) - 10*cos(2*pi*y) + 20')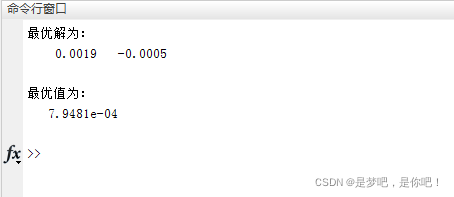

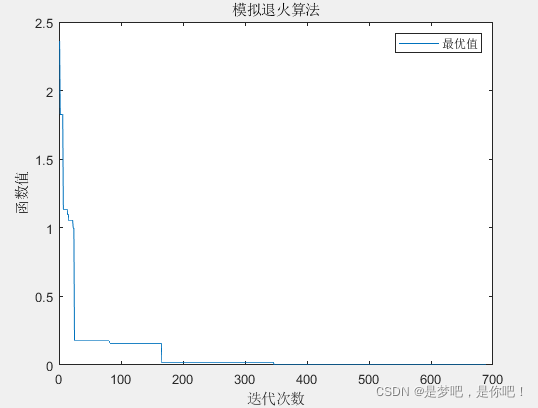
иҝҷйҮҢжңүдёҖдёӘеҫ…е°қиҜ•зҡ„жғіжі•пјҢе…Ҳз”Ёи’ҷзү№еҚЎжҙӣ/жЁЎжӢҹйҖҖзҒ«иҝӯд»ЈеҮ ж¬Ўе…ЁеұҖеҺ»жүҫжңҖдјҳзҡ„еҢәеҹҹпјҢеҶҚйҖҡиҝҮе…¶д»–жңүеҗ‘жңҖдјҳйҖјиҝ‘иҝҮзЁӢзҡ„з®—жі•еҶҚиҝӣдёҖжӯҘеҜ»дјҳпјҢжҲ–и®ёдјҡеҫҲеӨ§зЁӢеәҰйҷҚдҪҺдә§з”ҹеұҖйғЁжңҖдјҳи§Јзҡ„жҰӮзҺҮгҖӮ
дёӢйқўжҳҜжЁЎжӢҹйҖҖзҒ«е’Ңи’ҷзү№еҚЎжҙӣеҜ№дёҠиҝ°еҮҪж•°еҜ»дјҳзҡ„зЁӢеәҸпјҢиҝӯд»Јж¬Ўж•°е·Іи®ҫдёәдёҖиҮҙпјҢеҸҜд»ҘжҖқиҖғдёӢдёӨз§ҚзЁӢеәҸеҶҷжі•зҡ„ж•ҲзҺҮгҖҒе…ұеҗҢзӮ№гҖҒзјәзӮ№гҖӮзҗҶи®әз ”з©¶и®Із©¶з»“жһңеҘҪпјҢе®һйҷ…еә”з”Ёж—ўиҰҒдҝқиҜҒз»“жһңеҘҪд№ҹиҰҒдҝқиҜҒзЁӢеәҸиҝҗз®—ж•ҲзҺҮгҖӮ
clear
clc
num=689000; %йў—зІ’жҖ»ж•°
n=2; %иҮӘеҸҳйҮҸдёӘж•°
sub=[-5,-5]; %иҮӘеҸҳйҮҸдёӢйҷҗ
up=[5,5]; %иҮӘеҸҳйҮҸдёҠйҷҗ
tu
x=zeros(num,n);
fx=zeros(num,1);
for i=1:num
for j=1:n
x(i,j)=(up(j)-sub(j))*rand+sub(j);
end
fx(i,1)=fun(x(i,1),x(i,2));
end
[bestf,a]=min(fx);
bestx=x(a,:);
disp('жңҖдјҳи§Јдёәпјҡ')
disp(bestx)
disp('жңҖдјҳеҖјдёәпјҡ')
disp(bestf)
hold on
plot3(bestx(1),bestx(2),bestf,'ro','LineWidth',5)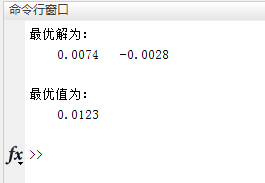
ж•ҲжһңзЎ®е®һеҖјеҫ—е•ҶжҰ·гҖӮ
д»ҘдёҠжҳҜвҖңеҰӮдҪ•дҪҝз”ЁPythonе’ҢMatlaе®һзҺ°жЁЎжӢҹйҖҖзҒ«жі•вҖқиҝҷзҜҮж–Үз« зҡ„жүҖжңүеҶ…е®№пјҢж„ҹи°ўеҗ„дҪҚзҡ„йҳ…иҜ»пјҒзӣёдҝЎеӨ§е®¶йғҪжңүдәҶдёҖе®ҡзҡ„дәҶи§ЈпјҢеёҢжңӣеҲҶдә«зҡ„еҶ…е®№еҜ№еӨ§е®¶жңүжүҖеё®еҠ©пјҢеҰӮжһңиҝҳжғіеӯҰд№ жӣҙеӨҡзҹҘиҜҶпјҢж¬ўиҝҺе…іжіЁдәҝйҖҹдә‘иЎҢдёҡиө„и®Ҝйў‘йҒ“пјҒ
е…ҚиҙЈеЈ°жҳҺпјҡжң¬з«ҷеҸ‘еёғзҡ„еҶ…е®№пјҲеӣҫзүҮгҖҒи§Ҷйў‘е’Ңж–Үеӯ—пјүд»ҘеҺҹеҲӣгҖҒиҪ¬иҪҪе’ҢеҲҶдә«дёәдё»пјҢж–Үз« и§ӮзӮ№дёҚд»ЈиЎЁжң¬зҪ‘з«ҷз«ӢеңәпјҢеҰӮжһңж¶үеҸҠдҫөжқғиҜ·иҒ”зі»з«ҷй•ҝйӮ®з®ұпјҡis@yisu.comиҝӣиЎҢдёҫжҠҘпјҢ并жҸҗдҫӣзӣёе…іиҜҒжҚ®пјҢдёҖз»ҸжҹҘе®һпјҢе°Ҷз«ӢеҲ»еҲ йҷӨж¶үе«ҢдҫөжқғеҶ…е®№гҖӮ
жӮЁеҘҪпјҢзҷ»еҪ•еҗҺжүҚиғҪдёӢи®ўеҚ•е“ҰпјҒ