您好,登录后才能下订单哦!
本篇内容介绍了“Python下的Matlab函数对应关系是什么”的有关知识,在实际案例的操作过程中,不少人都会遇到这样的困境,接下来就让小编带领大家学习一下如何处理这些情况吧!希望大家仔细阅读,能够学有所成!
首先给出官网链接,其中详细说明了在Python下如何用Numpy实现Matlab下相同的函数功能。
博主在用Python撰写代码的时候,想用Python实现在Matlab下某个函数的功能(比如Repmat函数),但是当使用语句
from numpy.matlib import repmat A = repmat(B, 1, 2)
调用工具包时,虽然可以正常实现功能,但是PyCharm下报出警告:
Importing from numpy.matlib is deprecated since 1.19.0. The matrix subclass is not the recommended way to represent matrices or deal with linear algebra (see https://docs.scipy.org/doc/numpy/user/numpy-for-matlab-users.html). Please adjust your code to use regular ndarray.
随后,通过查阅资料,发现是因为从1.19.0版本后,numpy就不再推荐使用numpy.matlib来实现对应功能了。
因此,大家可以对照官网上的说明来实现替换。
这里截取一小部分:
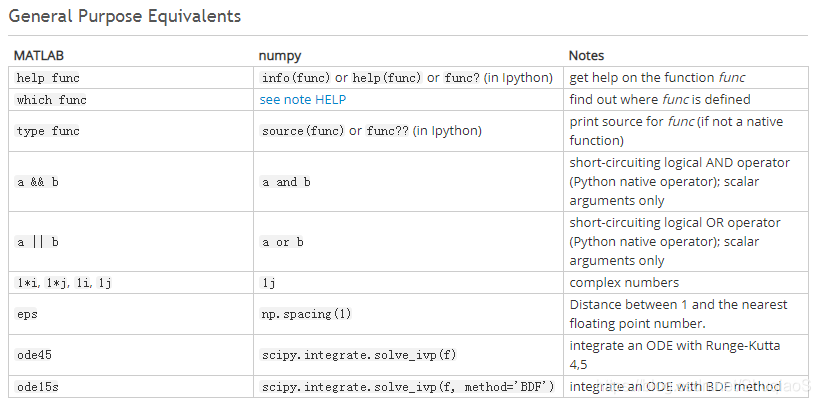
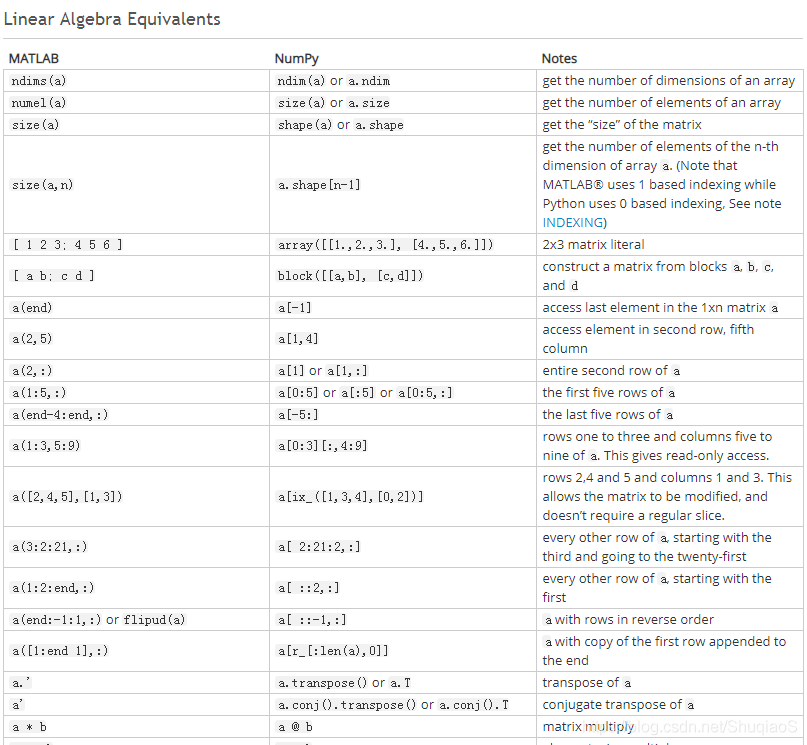
其他的可以从官网上面找到。
在日常使用中,matlab作为我们机器学习以及深度学习的模型训练使用的工具,而线上使用python实现模型落地。因为不可避免常遇到matlab与numpy之间有些操作需要相互转换。
| MATLAB | numpy | 说明 |
| helpfunc | info(func) or help(func) orfunc? (in Ipython) | 获得函数的帮助 |
| whichfunc | see note HELP | 查找函数的定义 |
| typefunc | source(func) or func?? (inIpython) | 查看函数源码 |
| a && b | a and b | 逻辑运算与操作 |
| a || b | a or b | 逻辑运算或操作 |
| 1*i, 1*j,1i, 1j | 1j | 复数 |
| eps | np.spacing(1) | 1与最小浮点数的距离 |
| ode45 | scipy.integrate.solve_ivp(f) | 求解同阶微分方程-Kutta 4,5 |
| ode15s | scipy.integrate.solve_ivp(f, method='BDF') | 求解变阶微分方程 |
| MATLAB | NumPy |
| ndims(a) | ndim(a) or a.ndim |
| numel(a) | size(a) or a.size |
| size(a) | shape(a) or a.shape |
| size(a,n) | a.shape[n-1] |
| [ 1 2 3; 4 5 6 ] | array([[1.,2.,3.], [4.,5.,6.]]) |
| [ a b; c d ] | vstack([hstack([a,b]), hstack([c,d])]) or bmat('a b; c d') |
| a(end) | a[-1] |
| a(2,5) | a[1,4] |
| a(2,:) | a[1] or a[1,:] |
| a(1:5,:) | a[0:5] or a[:5] or a[0:5,:] |
| a(end-4:end,:) | a[-5:] |
| a(1:3,5:9) | a[0:3][:,4:9] |
| a([2,4,5],[1,3]) | a[ix_([1,3,4],[0,2])] |
| a(3:2:21,:) | a[ 2:21:2,:] |
| a(1:2:end,:) | a[ ::2,:] |
| a(end:-1:1,:) or flipud(a) | a[ ::-1,:] |
| a([1:end 1],:) | a[r_[:len(a),0]] |
| a.' | a.transpose() or a.T |
| a' | a.conj().transpose() or a.conj().T |
| a * b | a.dot(b) |
| a .* b | a * b |
| a./b | a/b |
| a.^3 | a**3 |
| (a>0.5) | (a>0.5) |
| find(a>0.5) | nonzero(a>0.5) |
| a(:,find(v>0.5)) | a[:,nonzero(v>0.5)[0]] |
| a(:,find(v>0.5)) | a[:,v.T>0.5] |
| a(a<0.5)=0 | a[a<0.5]=0 |
| a .* (a>0.5) | a * (a>0.5) |
| a(:) = 3 | a[:] = 3 |
| y=x | y = x.copy() |
| y=x(2,:) | y = x[1,:].copy() |
| y=x(:) | y = x.flatten() |
| 1:10 | arange(1.,11.) or r_[1.:11.] or r_[1:10:10j] |
| 0:9 | arange(10.) or r_[:10.] or r_[:9:10j] |
| [1:10]' | arange(1.,11.)[:, newaxis] |
| zeros(3,4) | zeros((3,4)) |
| zeros(3,4,5) | zeros((3,4,5)) |
| ones(3,4) | ones((3,4)) |
| eye(3) | eye(3) |
| diag(a) | diag(a) |
| diag(a,0) | diag(a,0) |
| rand(3,4) | random.rand(3,4) |
| linspace(1,3,4) | linspace(1,3,4) |
| [x,y]=meshgrid(0:8,0:5) | mgrid[0:9.,0:6.] or meshgrid(r_[0:9.],r_[0:6.] |
| ogrid[0:9.,0:6.] or ix_(r_[0:9.],r_[0:6.] | |
| [x,y]=meshgrid([1,2,4],[2,4,5]) | meshgrid([1,2,4],[2,4,5]) |
| ix_([1,2,4],[2,4,5]) | |
| repmat(a, m, n) | tile(a, (m, n)) |
| [a b] | concatenate((a,b),1) or hstack((a,b)) or column_stack((a,b)) |
| [a; b] | concatenate((a,b)) or vstack((a,b)) or r_[a,b] |
| max(max(a)) | a.max() |
| max(a) | a.max(0) |
| max(a,[],2) | a.max(1) |
| max(a,b) | maximum(a, b) |
| norm(v) | sqrt(dot(v,v)) or np.linalg.norm(v) |
| a & b | logical_and(a,b) |
| a | b | logical_or(a,b) |
| bitand(a,b) | a & b |
| bitor(a,b) | a | b |
| inv(a) | linalg.inv(a) |
| pinv(a) | linalg.pinv(a) |
| rank(a) | linalg.matrix_rank(a) |
| a\b | linalg.solve(a,b) if a is square; linalg.lstsq(a,b) otherwise |
| b/a | Solve a.T x.T = b.T instead |
| [U,S,V]=svd(a) | U, S, Vh = linalg.svd(a), V = Vh.T |
| chol(a) | linalg.cholesky(a).T |
| [V,D]=eig(a) | D,V = linalg.eig(a) |
| [V,D]=eig(a,b) | V,D = np.linalg.eig(a,b) |
| [V,D]=eigs(a,k) | |
| [Q,R,P]=qr(a,0) | Q,R = scipy.linalg.qr(a) |
| [L,U,P]=lu(a) | L,U = scipy.linalg.lu(a) or LU,P=scipy.linalg.lu_factor(a) |
| conjgrad | scipy.sparse.linalg.cg |
| fft(a) | fft(a) |
| ifft(a) | ifft(a) |
| sort(a) | sort(a) or a.sort() |
| [b,I] = sortrows(a,i) | I = argsort(a[:,i]), b=a[I,:] |
| regress(y,X) | linalg.lstsq(X,y) |
| decimate(x, q) | scipy.signal.resample(x, len(x)/q) |
| unique(a) | unique(a) |
| squeeze(a) | a.squeeze() |
“Python下的Matlab函数对应关系是什么”的内容就介绍到这里了,感谢大家的阅读。如果想了解更多行业相关的知识可以关注亿速云网站,小编将为大家输出更多高质量的实用文章!
免责声明:本站发布的内容(图片、视频和文字)以原创、转载和分享为主,文章观点不代表本网站立场,如果涉及侵权请联系站长邮箱:is@yisu.com进行举报,并提供相关证据,一经查实,将立刻删除涉嫌侵权内容。