жӮЁеҘҪпјҢзҷ»еҪ•еҗҺжүҚиғҪдёӢи®ўеҚ•е“ҰпјҒ
иҝҷзҜҮж–Үз« дё»иҰҒи®Іи§ЈдәҶвҖңC++ RBTreeзәўй»‘ж ‘зҡ„жҖ§иҙЁдёҺе®һзҺ°ж–№жі•жҳҜд»Җд№ҲвҖқпјҢж–Үдёӯзҡ„и®Іи§ЈеҶ…е®№з®ҖеҚ•жё…жҷ°пјҢжҳ“дәҺеӯҰд№ дёҺзҗҶи§ЈпјҢдёӢйқўиҜ·еӨ§е®¶и·ҹзқҖе°Ҹзј–зҡ„жҖқи·Ҝж…ўж…ўж·ұе…ҘпјҢдёҖиө·жқҘз ”з©¶е’ҢеӯҰд№ вҖңC++ RBTreeзәўй»‘ж ‘зҡ„жҖ§иҙЁдёҺе®һзҺ°ж–№жі•жҳҜд»Җд№ҲвҖқеҗ§пјҒ
зәўй»‘ж ‘пјҢжҳҜдёҖз§ҚдәҢеҸүжҗңзҙўж ‘пјҢдҪҶеңЁжҜҸдёӘз»“зӮ№дёҠеўһеҠ дёҖдёӘеӯҳеӮЁдҪҚиЎЁзӨәз»“зӮ№зҡ„йўңиүІпјҢеҸҜд»ҘжҳҜRedжҲ–BlackгҖӮ йҖҡиҝҮеҜ№д»»дҪ•дёҖжқЎд»Һж №еҲ°еҸ¶еӯҗзҡ„и·Ҝеҫ„дёҠеҗ„дёӘз»“зӮ№зқҖиүІж–№ејҸзҡ„йҷҗеҲ¶пјҢзәўй»‘ж ‘зЎ®дҝқжІЎжңүдёҖжқЎи·Ҝеҫ„дјҡжҜ”е…¶д»–и·Ҝеҫ„й•ҝеҮәдҝ©еҖҚпјҢеӣ иҖҢжҳҜе№іиЎЎзҡ„ гҖӮпјҲж—ўжңҖй•ҝи·Ҝеҫ„й•ҝеәҰдёҚи¶…иҝҮжңҖзҹӯи·Ҝеҫ„й•ҝеәҰзҡ„ 2 еҖҚпјү
ps:ж ‘зҡ„и·Ҝеҫ„жҳҜд»Һж №иҠӮзӮ№иө°еҲ°з©әиҠӮзӮ№пјҲжӯӨеӨ„дёәNIL иҠӮзӮ№пјүжүҚз®—дёҖжқЎи·Ҝеҫ„
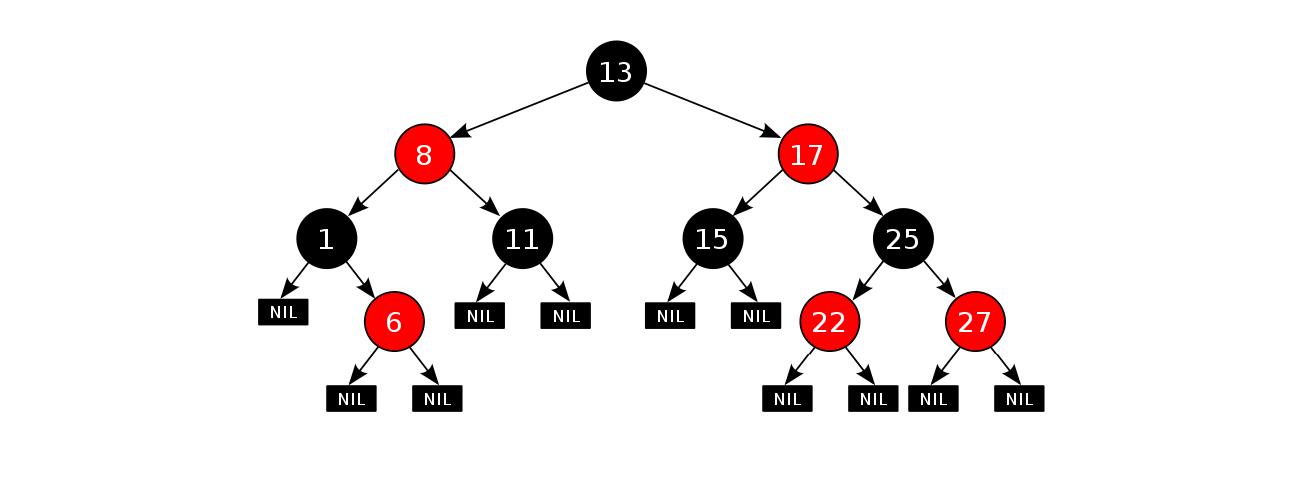
жҜҸдёӘз»“зӮ№дёҚжҳҜзәўиүІе°ұжҳҜй»‘иүІ
ж №з»“зӮ№жҳҜй»‘иүІзҡ„
еҰӮжһңдёҖдёӘз»“зӮ№жҳҜзәўиүІзҡ„пјҢеҲҷе®ғзҡ„дёӨдёӘеӯ©еӯҗз»“зӮ№жҳҜй»‘иүІзҡ„пјҲжІЎжңүиҝһз»ӯзҡ„зәўиүІз»“зӮ№пјү
еҜ№дәҺжҜҸдёӘз»“зӮ№пјҢд»ҺиҜҘиҠӮзӮ№еҲ°е…¶жүҖжңүеҗҺд»ЈеҸ¶з»“зӮ№зҡ„з®ҖеҚ•и·Ҝеҫ„дёҠпјҢеқҮеҢ…еҗ«зӣёеҗҢж•°зӣ®зҡ„й»‘иүІз»“зӮ№
жҜҸдёӘеҸ¶еӯҗз»“зӮ№йғҪжҳҜй»‘иүІзҡ„пјҲжӯӨеӨ„зҡ„еҸ¶еӯҗз»“зӮ№жҢҮзҡ„жҳҜз©әиҠӮзӮ№,NILиҠӮзӮ№пјүпјҢеҰӮжһңжҳҜз©әж ‘пјҢз©әиҠӮзӮ№д№ҹжҳҜй»‘иүІпјҢз¬ҰеҗҲ第дёҖдёӘжҖ§иҙЁ
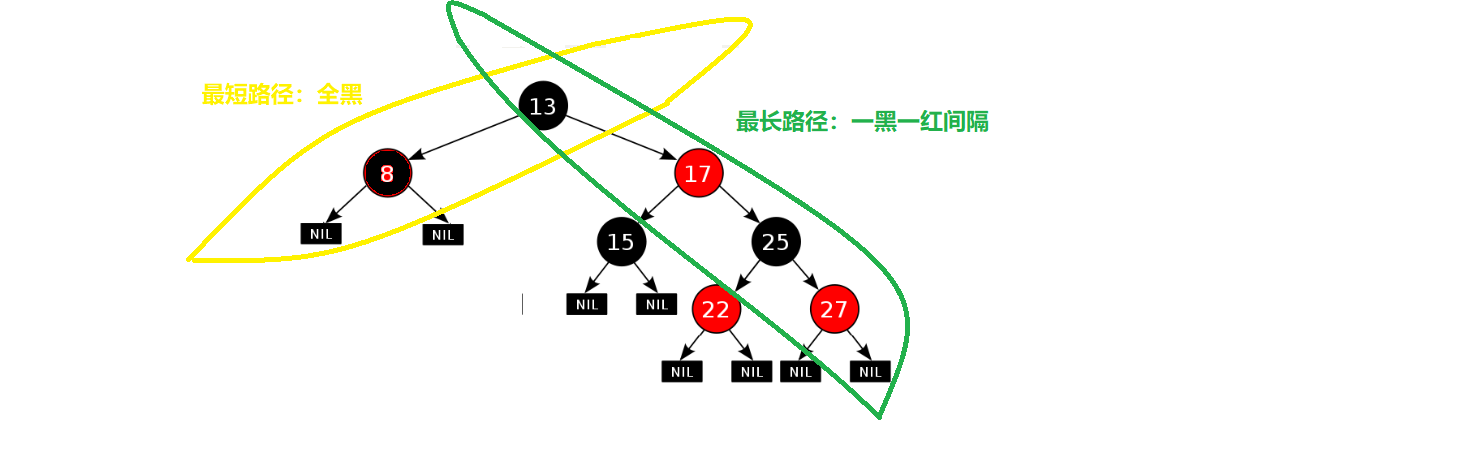
зҗҶи§ЈжңҖй•ҝи·Ҝеҫ„й•ҝеәҰдёҚи¶…иҝҮжңҖзҹӯи·Ҝеҫ„й•ҝеәҰзҡ„ 2 еҖҚпјҡ
ж №жҚ®з¬¬дёүдёӘжҖ§иҙЁпјҡзәўй»‘ж ‘дёҚдјҡеҮәзҺ°иҝһз»ӯзҡ„зәўиүІз»“зӮ№пјҢж №жҚ®з¬¬еӣӣдёӘжҖ§иҙЁпјҡд»ҺжҜҸдёӘз»“зӮ№еҲ°жүҖжңүеҗҺд»Јз»“зӮ№зҡ„и·Ҝеҫ„дёҠеҢ…еҗ«зӣёеҗҢж•°зӣ®зҡ„й»‘иүІз»“зӮ№гҖӮ
жһҒз«ҜеңәжҷҜпјҡжңҖзҹӯи·Ҝеҫ„дёҠе…Ёй»‘пјҢдёҖжқЎи·Ҝеҫ„й»‘иүІиҠӮзӮ№зҡ„ж•°йҮҸпјҢжңҖй•ҝи·Ҝеҫ„дёҠжҳҜдёҖй»‘дёҖзәўзӣёй—ҙзҡ„и·Ҝеҫ„
дёүеҸүй“ҫз»“жһ„пјҢеҜ№жҜ”AVLж•°иҠӮзӮ№зҡ„е®ҡд№үпјҢжҠҠе№іиЎЎеӣ еӯҗжӣҝжҚўжҲҗиҠӮзӮ№йўңиүІпјҢйҮҮз”Ёжһҡдёҫзҡ„ж–№ејҸпјҡ
//з»“зӮ№йўңиүІ
enum Color
{
RED,
BLACK,
};
template<class K, class V >
struct RBTreeNode
{
pair<K, V> _kv;
RBTreeNode<K, V>* _left;
RBTreeNode<K, V>* _right;
RBTreeNode<K, V>* _parent;
Color _col;
RBTreeNode(const pair<K,V>& kv)
:_kv(kv)
,_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_col(RED)
{}
};иҝҷйҮҢеҸҜд»Ҙжё…жҘҡзҡ„зңӢеҲ°пјҢжһ„йҖ з»“зӮ№ж—¶й»ҳи®Өи®ҫзҪ®дёәзәўиүІ,й—®йўҳжқҘдәҶпјҡ
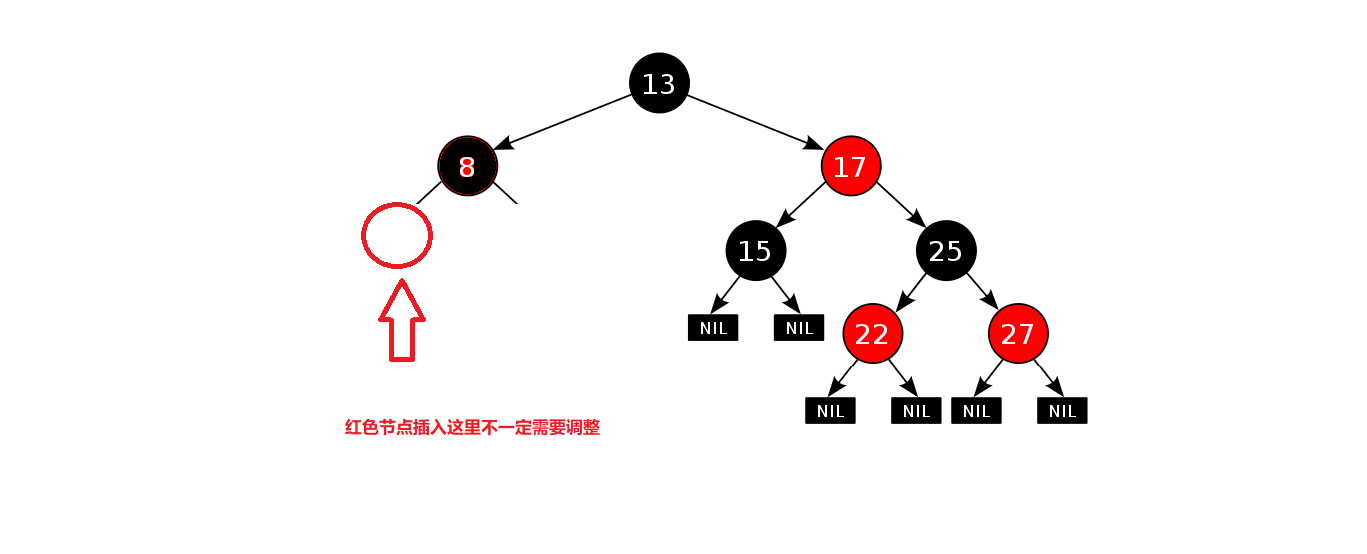
еҰӮжһңжҸ’е…Ҙзҡ„жҳҜй»‘иүІз»“зӮ№йӮЈе°ұжҳҜдёҚз¬ҰеҗҲ第еӣӣдёӘжҖ§иҙЁпјҲи·Ҝеҫ„дёҠеқҮеҢ…еҗ«зӣёеҗҢзҡ„й»‘иүІз»“зӮ№пјүпјҢжӯӨж—¶жҲ‘们еҝ…йЎ»иҰҒеҺ»иҝӣиЎҢз»ҙжҠӨжҜҸжқЎи·Ҝеҫ„зҡ„й»‘иүІз»“зӮ№
еҰӮжһңжҸ’е…Ҙзҡ„жҳҜзәўиүІз»“зӮ№йӮЈе°ұжҳҜдёҚз¬ҰеҗҲ第дёүдёӘжҖ§иҙЁпјҲжІЎжңүеҮәзҺ°иҝһз»ӯзҡ„зәўиүІз»“зӮ№пјүпјҢдҪҶжҳҜжҲ‘们并дёҚдёҖе®ҡйңҖиҰҒи°ғж•ҙпјҢеҰӮжһңж №еҲҡеҘҪдёәй»‘иүІпјҢе°ұдёҚйңҖиҰҒиҝӣиЎҢи°ғж•ҙгҖӮ
жүҖд»ҘеҰӮжһңжҸ’е…ҘдёәзәўиүІз»“зӮ№пјҢдёҚдёҖе®ҡдјҡз ҙеқҸз»“жһ„пјҢдҪҶжҳҜеҰӮжһңжҸ’е…Ҙй»‘иүІз»“зӮ№жҲ‘们е°ұеҝ…йЎ»еҺ»иҝӣиЎҢз»ҙжҠӨдәҶ
зәўй»‘ж ‘жҸ’е…Ҙзҡ„ж“ҚдҪңйғЁеҲҶе’ҢAVLж ‘зҡ„жҸ’е…ҘдёҖж ·пјҡ
жүҫеҲ°еҫ…жҸ’е…ҘдҪҚзҪ®
е°Ҷеҫ…жҸ’е…Ҙз»“зӮ№жҸ’е…ҘеҲ°ж ‘дёӯ
и°ғж•ҙпјҡиӢҘжҸ’е…Ҙз»“зӮ№зҡ„зҲ¶з»“зӮ№жҳҜзәўиүІзҡ„пјҢжҲ‘们е°ұйңҖиҰҒеҜ№зәўй»‘ж ‘иҝӣиЎҢи°ғж•ҙ
еүҚдёӨжӯҘеӨ§е·®дёҚе·®
еӣ дёәж–°иҠӮзӮ№зҡ„й»ҳи®ӨйўңиүІжҳҜзәўиүІпјҢеӣ жӯӨпјҡеҰӮжһңе…¶еҸҢдәІиҠӮзӮ№зҡ„йўңиүІжҳҜй»‘иүІпјҢжІЎжңүиҝқеҸҚзәўй»‘ж ‘д»»дҪ•жҖ§иҙЁпјҢеҲҷдёҚйңҖиҰҒи°ғж•ҙпјӣдҪҶеҪ“ж–°жҸ’е…ҘиҠӮзӮ№зҡ„еҸҢдәІиҠӮзӮ№йўңиүІдёәзәўиүІж—¶пјҢе°ұиҝқеҸҚдәҶжҖ§иҙЁдёүдёҚиғҪжңүиҝһеңЁдёҖиө·зҡ„зәўиүІиҠӮзӮ№пјҢжӯӨж—¶йңҖиҰҒеҜ№зәўй»‘ж ‘еҲҶжғ…еҶөжқҘи®Ёи®ә
е…ій”®еңЁдәҺеҜ№зәўй»‘ж ‘иҝӣиЎҢи°ғж•ҙпјҡдёәдәҶиғҪеӨҹеұ•зӨәеҮәеҗ„з§Қжғ…еҶөпјҢиҝҷйҮҢжңүдёҖдёӘеҹәжң¬зҡ„жЁЎеһӢпјҡ
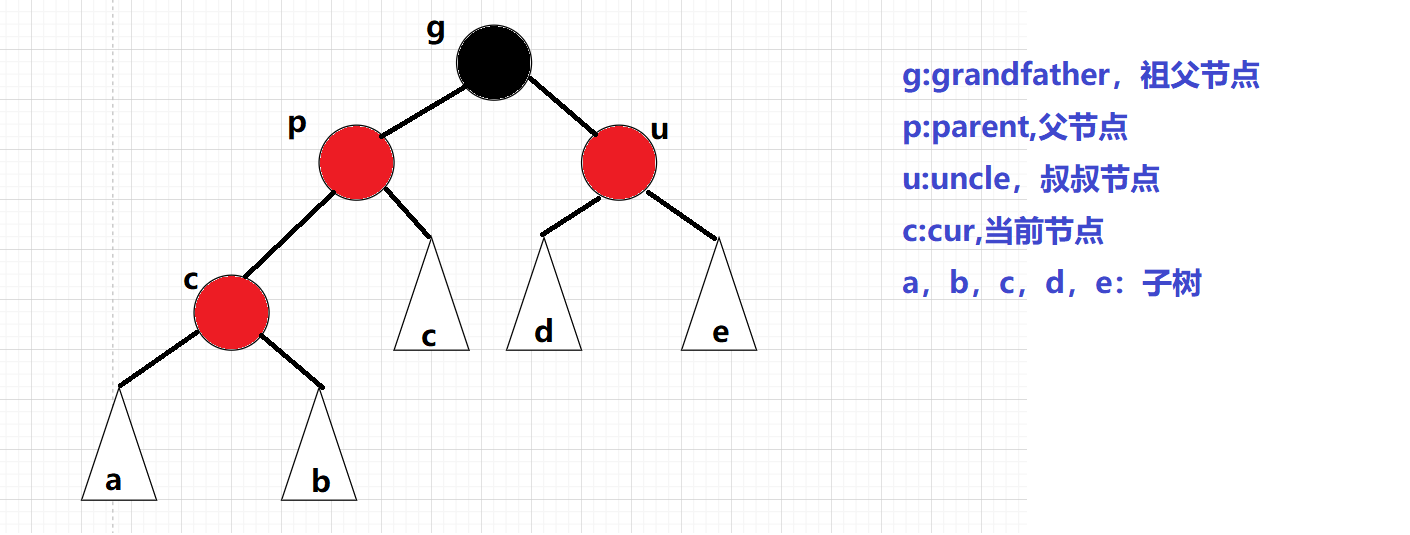
зәҰе®ҡ:curдёәеҪ“еүҚиҠӮзӮ№пјҢpдёәзҲ¶иҠӮзӮ№пјҢgдёәзҘ–зҲ¶иҠӮзӮ№пјҢuдёәеҸ”еҸ”иҠӮзӮ№
жғ…еҶөдёҖпјҡcurдёәзәўпјҢpдёәзәўпјҢgдёәй»‘пјҢuеӯҳеңЁдё”дёәзәў :
curдёәзәўпјҢpдёәзәўпјҢgдёәй»‘пјҢuеӯҳеңЁдё”дёәзәў
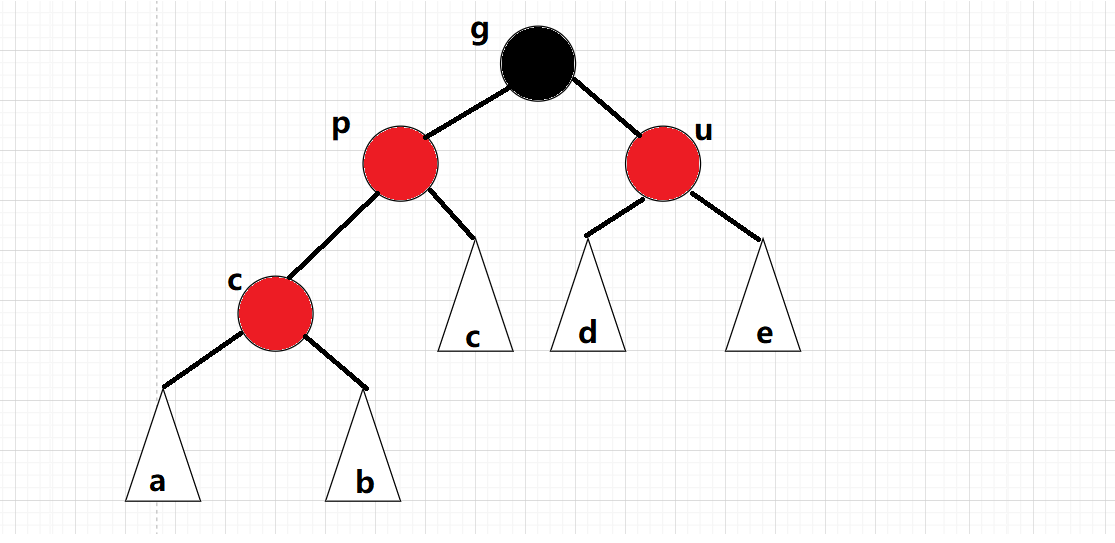
е…ій”®зңӢuз»“зӮ№пјҢж №з»“зӮ№зҡ„йўңиүІдёәй»‘иүІпјҢдёҚиғҪжңүиҝһз»ӯзҡ„зәўиүІз»“зӮ№пјҢжүҖд»ҘдёҠйқўзҡ„жғ…еҶөе·Із»ҸеҮәзҺ°иҝһз»ӯзҡ„зәўиүІз»“зӮ№дәҶпјҢжӯӨж—¶жҲ‘们йңҖиҰҒиҝӣиЎҢи°ғж•ҙпјҡ
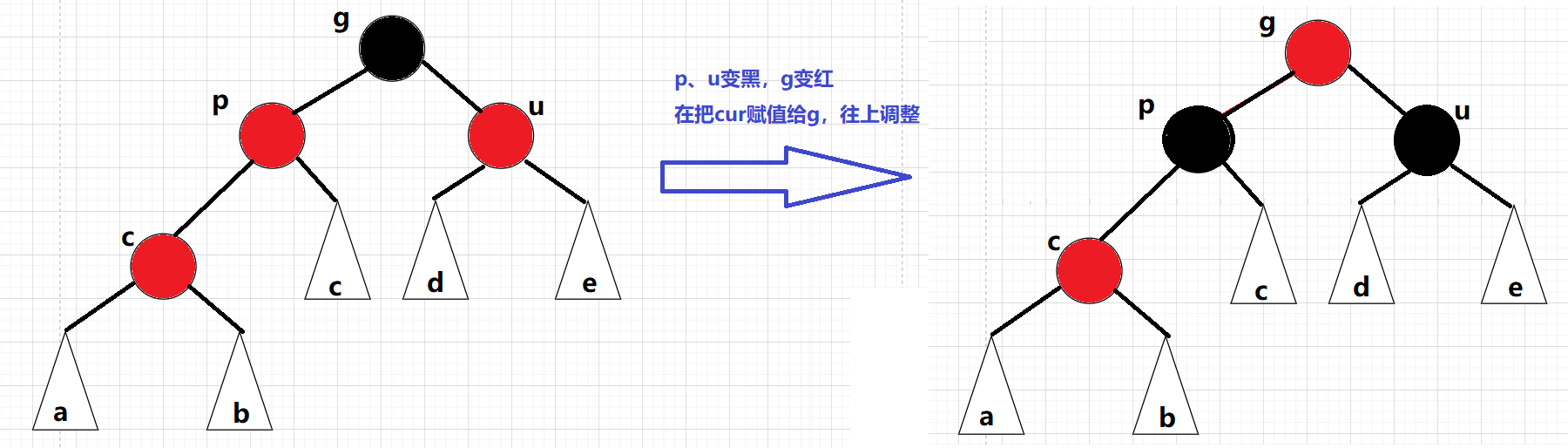
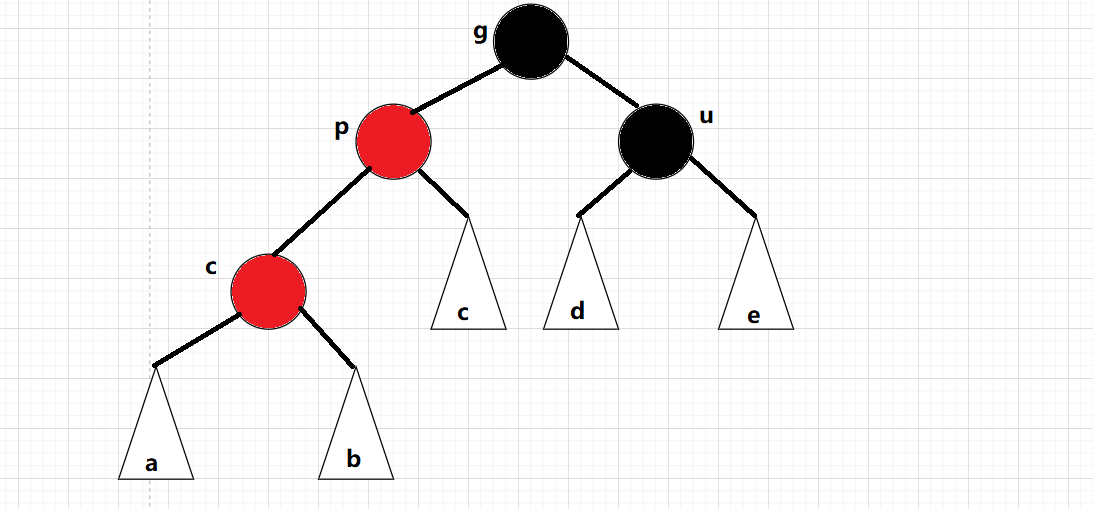
жҠҠpз»“зӮ№ж”№дёәй»‘иүІпјҢеҗҢж—¶жҠҠuз»“зӮ№д№ҹж”№дёәй»‘иүІпјҲз¬ҰеҗҲжҖ§иҙЁеӣӣпјҡжҜҸжқЎи·Ҝеҫ„дёҠзҡ„й»‘иүІиҠӮзӮ№ж•°йҮҸзӣёеҗҢпјүпјҢжңҖеҗҺеңЁжҠҠgз»“зӮ№ж”№дёәзәўиүІпјӣеҰӮжһңgжҳҜеӯҗж ‘зҡ„иҜқпјҢgдёҖе®ҡдјҡжңүеҸҢдәІпјҢдёәдәҶз»ҙжҢҒжҜҸжқЎи·Ҝеҫ„дёҠй»‘иүІиҠӮзӮ№зҡ„ж•°йҮҸпјҢgеҝ…йЎ»еҸҳзәўпјҢдёҚ然дјҡеӨҡеҮәдёҖдёӘй»‘иүІиҠӮзӮ№пјҢеңЁжҠҠgз»“зӮ№еҪ“еҒҡcurз»“зӮ№з»§з»ӯеҫҖдёҠи°ғж•ҙпјҢеҪ“gдёәж №з»“зӮ№ж—¶пјҢеңЁжҠҠgзҪ®дёәй»‘иүІпјҡ
д»Јз Ғе®һзҺ°пјҡ
while (parent && parent->_col == RED)
{
Node* grandfater = parent->_parent;
if (parent == grandfater->_left)
{
Node* uncle = grandfater->_right;
//жғ…еҶөдёҖпјҡuеӯҳеңЁдё”дёәзәў
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfater->_col = RED;
cur = grandfater;
parent = cur->_parent;
}
else//е…¶д»–жғ…еҶө
{
}
}
else//parent==grandfater->_right
{
Node* uncle = grandfater->_left;
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfater->_col = RED;
cur = grandfater;
parent = cur->_parent;
}
else
{
}
}
}
_root->_col = BLACK;жғ…еҶөдәҢпјҡcurдёәзәўпјҢpдёәзәўпјҢgдёәй»‘пјҢuдёҚеӯҳеңЁ/uдёәй»‘пјҢgpcеңЁеҗҢдёҖдҫ§пјҡ
жӯӨж—¶uзҡ„жғ…еҶөпјҡ
еҰӮжһңuз»“зӮ№дёҚеӯҳеңЁпјҢеҲҷcurдёҖе®ҡжҳҜж–°еўһз»“зӮ№пјҢеӣ дёәеҰӮжһңcurдёҚжҳҜж–°еўһз»“зӮ№пјҡеҲҷcurе’ҢpдёҖе®ҡжңүдёҖдёӘиҠӮзӮ№ж—¶й»‘иүІпјҢе°ұдёҚж»Ўи¶іжҜҸжқЎи·Ҝеҫ„йғҪжңүзӣёеҗҢзҡ„й»‘иүІз»“зӮ№зҡ„жҖ§иҙЁгҖӮ
еҰӮжһңuз»“зӮ№еӯҳеңЁпјҢеҲҷе…¶дёҖе®ҡжҳҜй»‘иүІзҡ„пјҢйӮЈд№ҲcиҠӮзӮ№еҺҹжқҘзҡ„йўңиүІдёҖе®ҡжҳҜй»‘иүІпјҢеңЁе…¶еӯҗж ‘и°ғж•ҙиҝҮзЁӢдёӯеҸҳдёәдәҶзәўиүІ
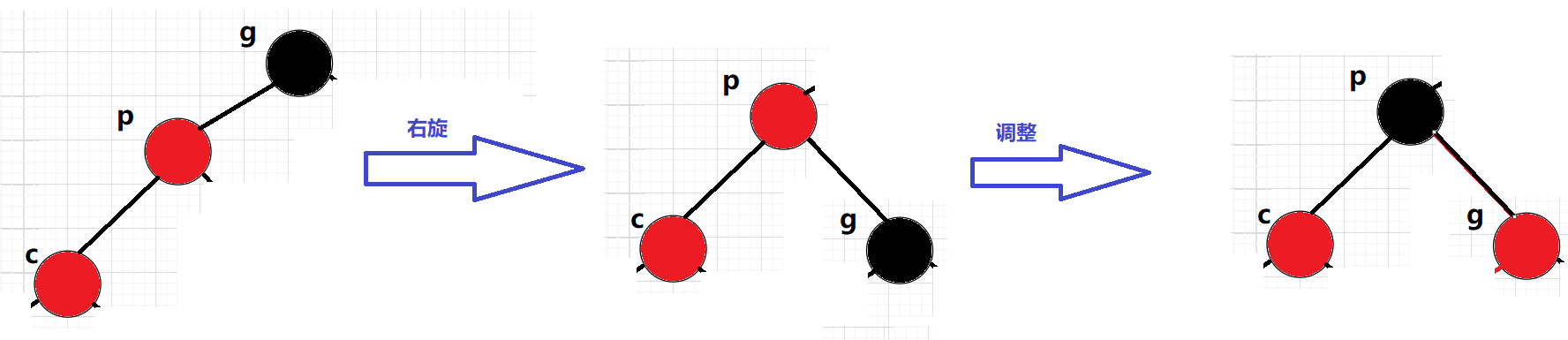
еҰӮжһңpдёәgзҡ„е·Ұеӯ©еӯҗпјҢcurдёәpзҡ„е·Ұеӯ©еӯҗпјҢеҲҷиҝӣиЎҢеҸіеҚ•ж—ӢиҪ¬пјӣ
еҰӮжһңpдёәgзҡ„еҸіеӯ©еӯҗпјҢcurдёәpзҡ„еҸіеӯ©еӯҗпјҢеҲҷиҝӣиЎҢе·ҰеҚ•ж—ӢиҪ¬пјҢ
еҗҢж—¶пјҢpгҖҒgеҸҳиүІ–pеҸҳй»‘пјҢgеҸҳзәў
д»ҘдёӢжғ…еҶөпјҡuдёҚеӯҳеңЁпјҢcurдёәж–°еўһиҠӮзӮ№пјҢиҝӣиЎҢеҸіеҚ•ж—Ӣпјҡ
д»ҘдёӢжғ…еҶөпјҡuз»“зӮ№еӯҳеңЁдё”дёәй»‘пјҡ
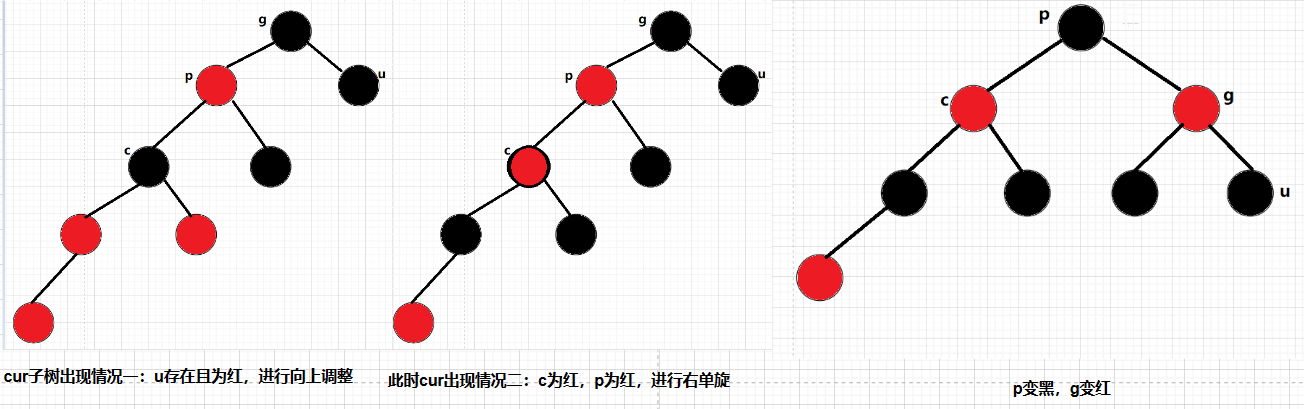
жғ…еҶөдёү: curдёәзәўпјҢpдёәзәўпјҢgдёәй»‘пјҢuдёҚеӯҳеңЁ/uдёәй»‘пјҢgpcдёҚеңЁеҗҢдёҖдҫ§:
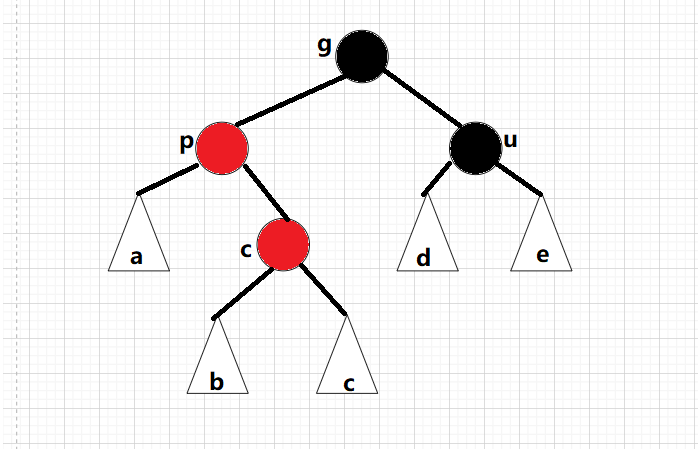
иҝҷж—¶еҖҷжҲ‘们е°ұйңҖиҰҒиҝӣиЎҢеҸҢж—ӢдәҶпјҡ
pдёәgзҡ„е·Ұеӯ©еӯҗпјҢcurдёәpзҡ„еҸіеӯ©еӯҗпјҢеҜ№pеҒҡе·ҰеҚ•ж—ӢиҪ¬пјӣ
pдёәgзҡ„еҸіеӯ©еӯҗпјҢcurдёәpзҡ„е·Ұеӯ©еӯҗпјҢеҜ№pеҒҡеҸіеҚ•ж—ӢиҪ¬; ж—ӢиҪ¬д№ӢеҗҺеҲҷиҪ¬жҚўжҲҗдәҶжғ…еҶө2пјҢеңЁз»§з»ӯиҝӣиЎҢи°ғж•ҙеҚіеҸҜ
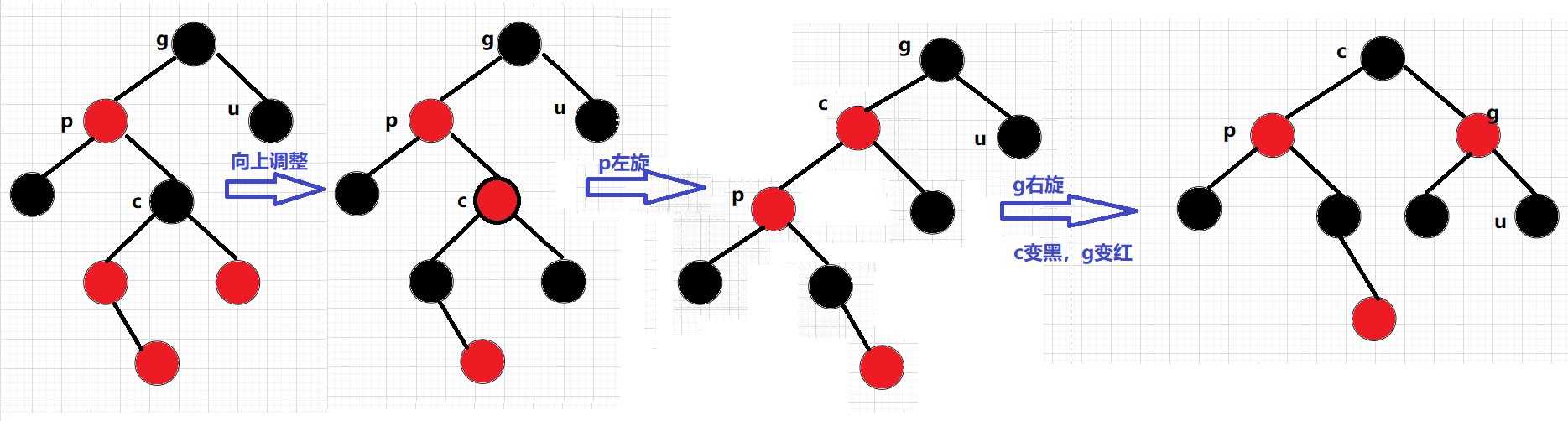
йҖҒдёҠжәҗз Ғпјҡ
#pragma once
#include <iostream>
#include <assert.h>
#include <time.h>
using namespace std;
enum Color
{
RED,
BLACK,
};
template<class K, class V >
struct RBTreeNode
{
pair<K, V> _kv;
RBTreeNode<K, V>* _left;
RBTreeNode<K, V>* _right;
RBTreeNode<K, V>* _parent;
Color _col;
RBTreeNode(const pair<K,V>& kv)
:_kv(kv)
,_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_col(RED)
{}
};
template<class K,class V>
class RBTree
{
typedef RBTreeNode<K, V> Node;
public:
bool Insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
_root->_col = BLACK;
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
cur->_col = RED;
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
cur->_parent = parent;
}
else
{
parent->_left = cur;
cur->_parent = parent;
}
while (parent && parent->_col == RED)
{
Node* grandfater = parent->_parent;
if (parent == grandfater->_left)
{
Node* uncle = grandfater->_right;
//жғ…еҶөдёҖпјҡuеӯҳеңЁдё”дёәзәў
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfater->_col = RED;
//еҗ‘дёҠи°ғж•ҙ
cur = grandfater;
parent = cur->_parent;
}
else
{
//жғ…еҶө2
if (cur == parent->_left)
{
RotateR(grandfater);
parent->_col = BLACK;
grandfater->_col = RED;
}
//жғ…еҶө3
else
{
// g
// p
// c
RotateL(parent);
RotateR(grandfater);
cur->_col = BLACK;
grandfater->_col = RED;
}
break;
}
}
else//parent==grandfater->_right
{
Node* uncle = grandfater->_left;
//жғ…еҶө1пјҡuеӯҳеңЁдё”дёәзәўиүІ
if (uncle && uncle->_col == RED)
{
uncle->_col = parent->_col = BLACK;
grandfater->_col = RED;
//еҗ‘дёҠи°ғж•ҙ
cur = grandfater;
parent = cur->_parent;
}
else
{
//жғ…еҶө2пјҡuдёҚеӯҳеңЁ/uеӯҳеңЁдёәй»‘иүІ
//g
// p
// c
if (cur == parent->_right)
{
RotateL(grandfater);
grandfater->_col = RED;
parent->_col = BLACK;
}
//жғ…еҶө3
// g
// p
// c
else
{
RotateR(parent);
RotateL(grandfater);
cur->_col = BLACK;
grandfater->_col = RED;
}
break;
}
}
}
//ж №еҸҳй»‘
_root->_col = BLACK;
return true;
}
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
Node* ppNode = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
if (ppNode == nullptr)
{
_root = subR;
_root->_parent = nullptr;
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = subR;
}
else
{
ppNode->_right = subR;
}
subR->_parent = ppNode;
}
}
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
Node* ppNode = parent->_parent;
parent->_parent = subL;
subL->_right = parent;
if (ppNode == nullptr)
{
_root = subL;
_root->_parent = nullptr;
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = subL;
}
else
{
ppNode->_right = subL;
}
subL->_parent = ppNode;
}
}
void InOrder()
{
_InOrder(_root);
}
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_kv.first << ":" << root->_kv.second << endl;
_InOrder(root->_right);
}
bool Check(Node*root,int blackNum,int ref)
{
if (root == nullptr)
{
//cout << blackNum << endl;
if (blackNum != ref)
{
cout << "иҝқеҸҚ规еҲҷпјҡжң¬жқЎи·Ҝеҫ„зҡ„й»‘иүІз»“зӮ№зҡ„ж•°йҮҸж №жңҖе·Ұи·Ҝеҫ„дёҚзӣёзӯү" << endl;
return false;
}
return true;
}
if (root->_col == RED && root->_parent->_col == RED)
{
cout << "иҝқеҸҚ规еҲҷпјҡеҮәзҺ°иҝһз»ӯзҡ„зәўиүІз»“зӮ№" << endl;
return false;
}
if (root->_col == BLACK)
{
++blackNum;
}
return Check(root->_left,blackNum,ref)
&& Check(root->_right,blackNum,ref);
}
bool IsBalance()
{
if (_root == nullptr)
{
return true;
}
if (_root->_col != BLACK)
{
return false;
}
int ref = 0;
Node* left = _root;
while (left)
{
if (left->_col == BLACK)
{
++ref;
}
left = left->_left;
}
return Check(_root,0,ref);
}
private:
Node* _root = nullptr;
};
void TestRBTree1()
{
//int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
RBTree<int, int> t;
for (auto e : a)
{
t.Insert(make_pair(e, e));
}
t.InOrder();
cout << t.IsBalance() << endl;
}
void TestRBTree2()
{
srand(time(0));
const size_t N = 100000;
RBTree<int, int> t;
for (size_t i = 0; i < N; i++)
{
size_t x = rand();
t.Insert(make_pair(x, x));
}
cout << t.IsBalance() << endl;
}ж„ҹи°ўеҗ„дҪҚзҡ„йҳ…иҜ»пјҢд»ҘдёҠе°ұжҳҜвҖңC++ RBTreeзәўй»‘ж ‘зҡ„жҖ§иҙЁдёҺе®һзҺ°ж–№жі•жҳҜд»Җд№ҲвҖқзҡ„еҶ…е®№дәҶпјҢз»ҸиҝҮжң¬ж–Үзҡ„еӯҰд№ еҗҺпјҢзӣёдҝЎеӨ§е®¶еҜ№C++ RBTreeзәўй»‘ж ‘зҡ„жҖ§иҙЁдёҺе®һзҺ°ж–№жі•жҳҜд»Җд№ҲиҝҷдёҖй—®йўҳжңүдәҶжӣҙж·ұеҲ»зҡ„дҪ“дјҡпјҢе…·дҪ“дҪҝз”Ёжғ…еҶөиҝҳйңҖиҰҒеӨ§е®¶е®һи·өйӘҢиҜҒгҖӮиҝҷйҮҢжҳҜдәҝйҖҹдә‘пјҢе°Ҹзј–е°ҶдёәеӨ§е®¶жҺЁйҖҒжӣҙеӨҡзӣёе…ізҹҘиҜҶзӮ№зҡ„ж–Үз« пјҢж¬ўиҝҺе…іжіЁпјҒ
е…ҚиҙЈеЈ°жҳҺпјҡжң¬з«ҷеҸ‘еёғзҡ„еҶ…е®№пјҲеӣҫзүҮгҖҒи§Ҷйў‘е’Ңж–Үеӯ—пјүд»ҘеҺҹеҲӣгҖҒиҪ¬иҪҪе’ҢеҲҶдә«дёәдё»пјҢж–Үз« и§ӮзӮ№дёҚд»ЈиЎЁжң¬зҪ‘з«ҷз«ӢеңәпјҢеҰӮжһңж¶үеҸҠдҫөжқғиҜ·иҒ”зі»з«ҷй•ҝйӮ®з®ұпјҡis@yisu.comиҝӣиЎҢдёҫжҠҘпјҢ并жҸҗдҫӣзӣёе…іиҜҒжҚ®пјҢдёҖз»ҸжҹҘе®һпјҢе°Ҷз«ӢеҲ»еҲ йҷӨж¶үе«ҢдҫөжқғеҶ…е®№гҖӮ
жӮЁеҘҪпјҢзҷ»еҪ•еҗҺжүҚиғҪдёӢи®ўеҚ•е“ҰпјҒ