Leetcode-Single Number

Single NumberI

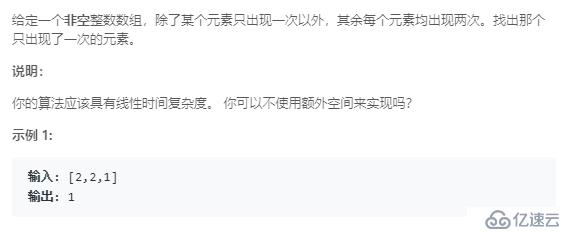
分析：这道题应该是很简单了，直接使用异或运算，把重复出现的数字消掉剩下的就是出现一次的元素

lass Solution {
    public int singleNumber(int[] nums) {
        int tmp = nums[0];
        for(int i = 1;i < nums.length;i++){
            tmp = tmp ^  nums[i];
        }
        return tmp;
    }
}

Single NumberII

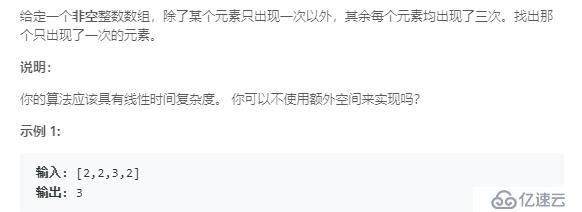
分析：这种题型可以归纳为一个数组中的元素某一元素只出现了K次，而其他元素均出现了M次，然后求出出现K次的元素问题。如果K

为奇数M为偶数，就跟上面第一题是一样的处理方式了；而其他情况则需要考虑使用位运算。我们知道，每个数字的二进制表示是一定的，所以我们通过计算每一位中1的个数，然后除3，若余数为0说明该位上为1的数都出现了三次，若余数不为0，说明我们要找的那个数字该位为1，通过移位运算实现上述过程。同理，若题目要求其他元素均出现了5次，就除5。

class Solution {
    public int singleNumber(int[] nums) {
        int ans = 0;
        for(int i = 0 ; i < 32 ; i++){
            int sum = 0;
            for(int j = 0 ; j < nums.length ; j++){
                if(((nums[j] >> i) & 1) == 1 ){
                    sum++;
                    sum %= 3;
                }
            }
            if(sum != 0){
                ans |= sum << i;//将循环中右移的位移回原位置
            }
        }
        return ans;
        
    }

Single NumberIII

分析：数组中的无关元素出现了偶数次，所以先考虑用异或将它们消除，得到3和5的异或结果。然后我们考虑如何将3和5分离：3（011）和5（101）异或的结果为6(110),我们需要先找到3和5的二进制表示中不相同的一位，这里的方法就是6与-6进行相与，即110与其补码(取反加一)011相与，得到010（即从右往左3和5的第二位不同），我们姑且将它称为分离因子。然后遍历整个数组，每个数与该分离因子相与可将数组分为&x==0和&x!=0的两组，然后在每组内部进行异或运算，得到结果。

class Solution {
    public int[] singleNumber(int[] nums) {
        int diff = 0;
        for(int num : nums) {
            diff ^= num;
        }
        diff &= -diff;
        int[] res = new int[]{0,0};
        for(int i : nums) {
            if((diff & i) == 0) {
                res[0] ^= i;
            }
            if((diff & i) != 0) {
                res[1] ^= i;
            }
        }
        return res;
    }
}