python 普通克里金（Kriging）法的实现

发布时间：2020-08-24 06:21:38 作者：山人青冥
来源：脚本之家阅读：533

克里金法时一种用于空间插值的地学统计方法。

克里金法用半变异测定空间要素，要素即自相关要素。

半变异公式为：

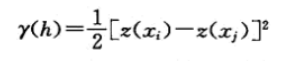
其中γ(h) 是已知点 xi 和 xj 的半变异，***h***表示这两个点之间的距离，z是属性值。

假设不存在漂移，普通克里金法重点考虑空间相关因素，并用拟合的半变异直接进行插值。

估算某测量点z值的通用方程为：

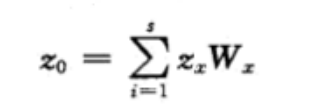
python 普通克里金（Kriging）法的实现

式中，z0是待估计值，zx是已知点x的值，Wx是每个已知点关联的权重，s是用于估计的已知点数目。
权重可以由一组矩阵方程得到。

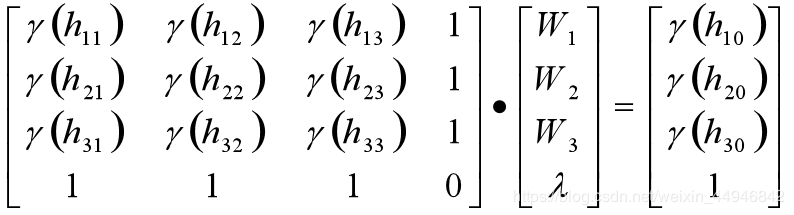
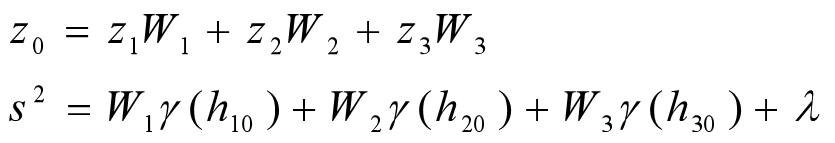
python 普通克里金（Kriging）法的实现

此程序对半变异进行拟合时采用的时最简单的正比例函数拟合

数据为csv格式

保存格式如下：

第一行为第一个点以此类推

最后一行是待求点坐标，其中z为未知值，暂且假设为0

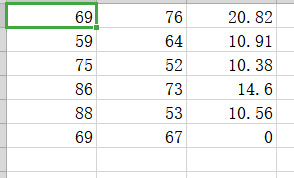
python 普通克里金（Kriging）法的实现

代码如下：

import numpy as np
from math import*
from numpy.linalg import *
h_data=np.loadtxt(open('高程点数据.csv'),delimiter=",",skiprows=0)
print('原始数据如下(x,y,z):\n未知点高程初值设为0\n',h_data)
def dis(p1,p2):
 a=pow((pow((p1[0]-p2[0]),2)+pow((p1[1]-p2[1]),2)),0.5)
 return a
def rh(z1,z2):
 r=1/2*pow((z1[2]-z2[2]),2)
 return r
def proportional(x,y):
 xx,xy=0,0
 for i in range(len(x)):
  xx+=pow(x[i],2)
  xy+=x[i]*y[i]
 k=xy/xx
 return k
r=[];pp=[];p=[];
for i in range(len(h_data)):
 pp.append(h_data[i])
for i in range(len(pp)):
 for j in range(len(pp)):
  p.append(dis(pp[i],pp[j]))
  r.append(rh(pp[i],pp[j]))
r=np.array(r).reshape(len(h_data),len(h_data))
r=np.delete(r,len(h_data)-1,axis =0)
r=np.delete(r,len(h_data)-1,axis =1)

h=np.array(p).reshape(len(h_data),len(h_data))
h=np.delete(h,len(h_data)-1,axis =0)
oh=h[:,len(h_data)-1]
h=np.delete(h,len(h_data)-1,axis =1)

hh=np.triu(h,0)
rr=np.triu(r,0)
r0=[];h0=[];
for i in range(len(h_data)-1):
 for j in range(len(h_data)-1):
  if hh[i][j] !=0:
   a=h[i][j]
   h0.append(a)
  if rr[i][j] !=0:
   a=rr[i][j]
   r0.append(a)
k=proportional(h0,r0)
hnew=h*k
a2=np.ones((1,len(h_data)-1))
a1=np.ones((len(h_data)-1,1))
a1=np.r_[a1,[[0]]]
hnew=np.r_[hnew,a2]
hnew=np.c_[hnew,a1]
print('半方差联立矩阵：\n',hnew)
oh=np.array(k*oh)
oh=np.r_[oh,[1]]
w=np.dot(inv(hnew),oh)
print('权阵运算结果：\n',w)
z0,s2=0,0
for i in range(len(h_data)-1):
 z0=w[i]*h_data[i][2]+z0
 s2=w[i]*oh[i]+s2
s2=s2+w[len(h_data)-1]
print('未知点高程值为：\n',z0)
print('半变异值为：\n',pow(s2,0.5))
input()

运算结果

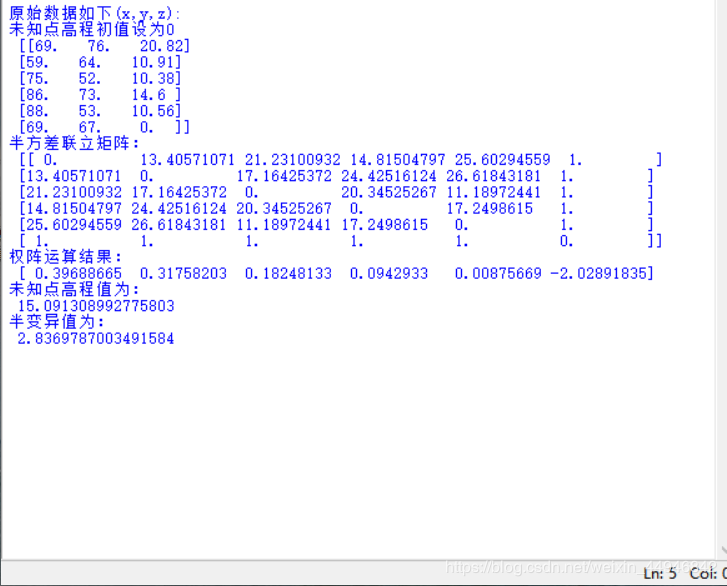
python 普通克里金（Kriging）法的实现

python初学，为了完成作业写了个小程序来帮助计算，因为初学知识有限，有很多地方写的很复杂，可以优化的地方很多。还望读者谅解，欢迎斧正谢谢！

参考文献：
【1】(美)张康聪著;陈健飞等译. 地理信息系统导论（第三版）. 北京：清华大学出版社, 2009.04.

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持亿速云。

python 普通克里金（Kriging）法的实现

相关阅读