жӮЁеҘҪпјҢзҷ»еҪ•еҗҺжүҚиғҪдёӢи®ўеҚ•е“ҰпјҒ
жң¬ж–Үе®һдҫӢи®Іиҝ°дәҶpythonе®һзҺ°зҡ„жұүиҜәеЎ”з®—жі•гҖӮеҲҶдә«з»ҷеӨ§е®¶дҫӣеӨ§е®¶еҸӮиҖғпјҢе…·дҪ“еҰӮдёӢпјҡ

规еҲҷпјҡ
еңҶзӣҳд»ҺдёӢйқўејҖе§ӢжҢүеӨ§е°ҸйЎәеәҸйҮҚж–°ж‘Ҷж”ҫеңЁеҸҰдёҖж №жҹұеӯҗдёҠгҖӮ并且规е®ҡ
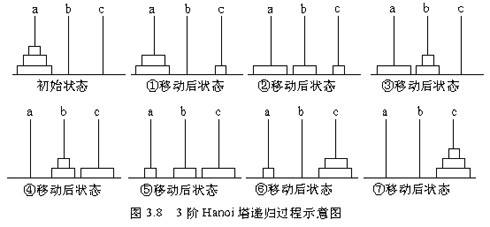
з®—жі•жҖқи·ҜпјҡгҖҗдёүйҳ¶зҡ„移еҠЁжҖқи·ҜгҖ‘
pythonе®һзҺ°пјҡ[жіЁж„Ҹе®һеҸӮе’ҢеҪўеҸӮ]
з”Ёpythonж–№жі•и°ғз”ЁпјҢе®һзҺ°иҫ“е…ҘеңҶзӣҳж•°пјҢжү“еҚ°з§»еҠЁзҡ„иҝҮзЁӢ
def move(n,a,b,c):
if n==1:
print(a,'-->',c)
else:
move(n-1,a,c,b) #е°ҶеүҚn-1дёӘзӣҳеӯҗд»Һa移еҠЁеҲ°bдёҠ
move(1,a,b,c) #е°ҶжңҖеә•дёӢзҡ„жңҖеҗҺдёҖдёӘзӣҳеӯҗд»Һa移еҠЁеҲ°cдёҠ
move(n-1,b,a,c) #е°ҶbдёҠзҡ„n-1дёӘзӣҳеӯҗ移еҠЁеҲ°cдёҠ
move(3,'A','B','C')
зЁӢеәҸжү§иЎҢзҡ„з»“жһңпјҡ
A --> C
A --> B
C --> B
A --> C
B --> A
B --> C
A --> C
зЁӢеәҸеҲҶжһҗпјҡ
ж¶үеҸҠеҲ°йҖ’еҪ’еҮҪж•°пјҢзҗҶи§Јиө·жқҘдјҡе®№жҳ“еҮҢд№ұпјҢжҲ‘们д»Ҙ3дёӘзӣҳеӯҗдёәдҫӢпјҢиҝӣиЎҢжү§иЎҢжӯҘйӘӨеҲҶжһҗ
(3,A,B,C)
->move(2,A,C,B)
->move(1,A,B,C) A->C
->move(1,A,C,B) A->B
->move(1,C,A,B) C->B
->move(1,A,B,C)
гҖҖгҖҖгҖҖгҖҖгҖҖгҖҖгҖҖгҖҖгҖҖгҖҖгҖҖгҖҖгҖҖгҖҖгҖҖгҖҖ A->C
->move(2,B,A,C)
->move(1,B,C,A) B->A
->move(1,B,A,C) B->C
->move(1,A,B,C) A->C
жӣҙеӨҡе…ідәҺPythonзӣёе…іеҶ…е®№ж„ҹе…ҙи¶Јзҡ„иҜ»иҖ…еҸҜжҹҘзңӢжң¬з«ҷдё“йўҳпјҡгҖҠPythonж•°жҚ®з»“жһ„дёҺз®—жі•ж•ҷзЁӢгҖӢгҖҒгҖҠPythonеҠ еҜҶи§ЈеҜҶз®—жі•дёҺжҠҖе·§жҖ»з»“гҖӢгҖҒгҖҠPythonзј–з Ғж“ҚдҪңжҠҖе·§жҖ»з»“гҖӢгҖҒгҖҠPythonеҮҪж•°дҪҝз”ЁжҠҖе·§жҖ»з»“гҖӢгҖҒгҖҠPythonеӯ—з¬ҰдёІж“ҚдҪңжҠҖе·§жұҮжҖ»гҖӢеҸҠгҖҠPythonе…Ҙй—ЁдёҺиҝӣйҳ¶з»Ҹе…ёж•ҷзЁӢгҖӢ
еёҢжңӣжң¬ж–ҮжүҖиҝ°еҜ№еӨ§е®¶PythonзЁӢеәҸи®ҫи®ЎжңүжүҖеё®еҠ©гҖӮ
е…ҚиҙЈеЈ°жҳҺпјҡжң¬з«ҷеҸ‘еёғзҡ„еҶ…е®№пјҲеӣҫзүҮгҖҒи§Ҷйў‘е’Ңж–Үеӯ—пјүд»ҘеҺҹеҲӣгҖҒиҪ¬иҪҪе’ҢеҲҶдә«дёәдё»пјҢж–Үз« и§ӮзӮ№дёҚд»ЈиЎЁжң¬зҪ‘з«ҷз«ӢеңәпјҢеҰӮжһңж¶үеҸҠдҫөжқғиҜ·иҒ”зі»з«ҷй•ҝйӮ®з®ұпјҡis@yisu.comиҝӣиЎҢдёҫжҠҘпјҢ并жҸҗдҫӣзӣёе…іиҜҒжҚ®пјҢдёҖз»ҸжҹҘе®һпјҢе°Ҷз«ӢеҲ»еҲ йҷӨж¶үе«ҢдҫөжқғеҶ…е®№гҖӮ
жӮЁеҘҪпјҢзҷ»еҪ•еҗҺжүҚиғҪдёӢи®ўеҚ•е“ҰпјҒ