жӮЁеҘҪпјҢзҷ»еҪ•еҗҺжүҚиғҪдёӢи®ўеҚ•е“ҰпјҒ
ARIMAжЁЎеһӢ
ARIMAжЁЎеһӢзҡ„е…Ёз§°жҳҜиҮӘеӣһеҪ’移еҠЁе№іеқҮжЁЎеһӢпјҢжҳҜз”ЁжқҘйў„жөӢж—¶й—ҙеәҸеҲ—зҡ„дёҖз§Қеёёз”Ёзҡ„з»ҹи®ЎжЁЎеһӢпјҢдёҖиҲ¬и®°дҪңARIMA(p,d,q)гҖӮ
ARIMAзҡ„йҖӮеә”жғ…еҶө
ARIMAжЁЎеһӢзӣёеҜ№жқҘиҜҙжҜ”иҫғз®ҖеҚ•жҳ“з”ЁгҖӮеңЁеә”з”ЁARIMAжЁЎеһӢж—¶пјҢиҰҒдҝқиҜҒд»ҘдёӢеҮ зӮ№пјҡ
еҲӨж–ӯж—¶еәҸж•°жҚ®зЁіе®ҡ
еҹәжң¬еҲӨж–ӯж–№жі•пјҡзЁіе®ҡзҡ„ж•°жҚ®пјҢжҖ»дҪ“дёҠжҳҜжІЎжңүдёҠеҚҮе’ҢдёӢйҷҚзҡ„и¶ӢеҠҝзҡ„пјҢжҳҜжІЎжңүе‘ЁжңҹжҖ§зҡ„пјҢж–№е·®и¶Ӣеҗ‘дәҺдёҖдёӘзЁіе®ҡзҡ„еҖјгҖӮ
ARIMAж•°еӯҰиЎЁиҫҫ
ARIMA(p,d,q)пјҢе…¶дёӯpжҳҜж•°жҚ®жң¬иә«зҡ„ж»һеҗҺж•°пјҢжҳҜARжЁЎеһӢеҚіиҮӘеӣһеҪ’жЁЎеһӢдёӯзҡ„еҸӮж•°гҖӮdжҳҜж—¶й—ҙеәҸеҲ—ж•°жҚ®йңҖиҰҒеҮ ж¬Ўе·®еҲҶжүҚиғҪеҫ—еҲ°зЁіе®ҡзҡ„ж•°жҚ®гҖӮqжҳҜйў„жөӢиҜҜе·®зҡ„ж»һеҗҺж•°пјҢжҳҜMAжЁЎеһӢеҚіж»‘еҠЁе№іеқҮжЁЎеһӢдёӯзҡ„еҸӮж•°гҖӮ
a) pеҸӮж•°дёҺARжЁЎеһӢ
ARжЁЎеһӢжҸҸиҝ°зҡ„жҳҜеҪ“еүҚеҖјдёҺеҺҶеҸІеҖјд№Ӣй—ҙзҡ„е…ізі»пјҢж»һеҗҺpйҳ¶зҡ„ARжЁЎеһӢеҸҜд»ҘиЎЁзӨәдёәпјҡ
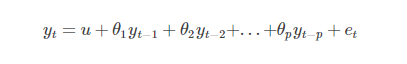
е…¶дёӯuжҳҜеёёж•°пјҢetд»ЈиЎЁиҜҜе·®гҖӮ
b) qеҸӮж•°дёҺMAжЁЎеһӢ
MAжЁЎеһӢжҸҸиҝ°зҡ„жҳҜеҪ“еүҚеҖјдёҺиҮӘеӣһеҪ’йғЁеҲҶзҡ„иҜҜе·®зҙҜи®Ўзҡ„е…ізі»пјҢж»һеҗҺqйҳ¶зҡ„MAжЁЎеһӢеҸҜд»ҘиЎЁзӨәдёәпјҡ
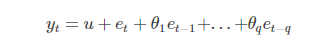
е…¶дёӯuжҳҜеёёж•°пјҢetд»ЈиЎЁиҜҜе·®гҖӮ
c) dеҸӮж•°дёҺе·®еҲҶ
дёҖйҳ¶е·®еҲҶпјҡ
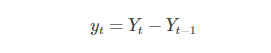
дәҢйҳ¶е·®еҲҶпјҡ
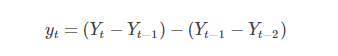
d) ARIMA = AR+MA
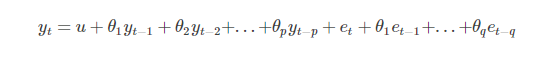
ARIMAжЁЎеһӢдҪҝз”ЁжӯҘйӘӨ

Pythonи°ғз”ЁARIMA
#е·®еҲҶеӨ„зҗҶ diff_series = diff_series.diff(1)#дёҖйҳ¶ diff_series2 = diff_series.diff(1)#дәҢйҳ¶ #ACFдёҺPACF #д»ҺscipyеҜје…ҘеҢ… from scipy import stats import statsmodels.api as sm #з”»еҮәacfе’Ңpacf sm.graphics.tsa.plot_acf(diff_series) sm.graphics.tsa.plot_pacf(diff_series) #arimaжЁЎеһӢ from statsmodels.tsa.arima_model import ARIMA model = ARIMA(train_data,order=(p,d,q),freq='')#freqжҳҜйў‘зҺҮ,ж №жҚ®ж•°жҚ®еЎ«еҶҷ arima = model.fit()#и®ӯз»ғ print(arima) pred = arima.predict(start='',end='')#йў„жөӢ
жҖ»з»“
д»ҘдёҠе°ұжҳҜиҝҷзҜҮж–Үз« зҡ„е…ЁйғЁеҶ…е®№дәҶпјҢеёҢжңӣжң¬ж–Үзҡ„еҶ…е®№еҜ№еӨ§е®¶зҡ„еӯҰд№ жҲ–иҖ…е·ҘдҪңе…·жңүдёҖе®ҡзҡ„еҸӮиҖғеӯҰд№ д»·еҖјпјҢи°ўи°ўеӨ§е®¶еҜ№дәҝйҖҹдә‘зҡ„ж”ҜжҢҒгҖӮеҰӮжһңдҪ жғідәҶи§ЈжӣҙеӨҡзӣёе…іеҶ…е®№иҜ·жҹҘзңӢдёӢйқўзӣёе…ій“ҫжҺҘ
е…ҚиҙЈеЈ°жҳҺпјҡжң¬з«ҷеҸ‘еёғзҡ„еҶ…е®№пјҲеӣҫзүҮгҖҒи§Ҷйў‘е’Ңж–Үеӯ—пјүд»ҘеҺҹеҲӣгҖҒиҪ¬иҪҪе’ҢеҲҶдә«дёәдё»пјҢж–Үз« и§ӮзӮ№дёҚд»ЈиЎЁжң¬зҪ‘з«ҷз«ӢеңәпјҢеҰӮжһңж¶үеҸҠдҫөжқғиҜ·иҒ”зі»з«ҷй•ҝйӮ®з®ұпјҡis@yisu.comиҝӣиЎҢдёҫжҠҘпјҢ并жҸҗдҫӣзӣёе…іиҜҒжҚ®пјҢдёҖз»ҸжҹҘе®һпјҢе°Ҷз«ӢеҲ»еҲ йҷӨж¶үе«ҢдҫөжқғеҶ…е®№гҖӮ
жӮЁеҘҪпјҢзҷ»еҪ•еҗҺжүҚиғҪдёӢи®ўеҚ•е“ҰпјҒ