您好,登录后才能下订单哦!
这期内容当中小编将会给大家带来有关使用python怎么实现梯度下降法,文章内容丰富且以专业的角度为大家分析和叙述,阅读完这篇文章希望大家可以有所收获。
1、简单易用,与C/C++、Java、C# 等传统语言相比,Python对代码格式的要求没有那么严格;2、Python属于开源的,所有人都可以看到源代码,并且可以被移植在许多平台上使用;3、Python面向对象,能够支持面向过程编程,也支持面向对象编程;4、Python是一种解释性语言,Python写的程序不需要编译成二进制代码,可以直接从源代码运行程序;5、Python功能强大,拥有的模块众多,基本能够实现所有的常见功能。
1.最简单的情况,样本只有一个变量,即简单的(x,y)。多变量的则可为使用体重或身高判断男女(这是假设,并不严谨),则变量有两个,一个是体重,一个是身高,则可表示为(x1,x2,y),即一个目标值有两个属性。
2.单个变量的情况最简单的就是,函数hk(x)=k*x这条直线(注意:这里k也是变化的,我们的目的就是求一个最优的 k)。而深度学习中,我们是不知道函数的,也就是不知道上述的k。 这里讨论单变量的情况:
在不知道k的情况下,我们是通过样本(x1,y1),(x2,y2),(xn,yn)来获取k。获取的k的好坏则有损失函数来衡量。
损失函数:就是你预测的值和真实值的差异大小(比如一个样本(1,1)他的真实值是1,而你预测的是0.5,则差异 比较大,如果你预测值为0.9999,则差异就比较小了)。
损失函数为定义如下(此处为单变量的情况)
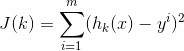
目的是求使损失函数最小的变量k(注意和变量x区分),则将损失函数对k求导(多变量时为求偏导得梯度,这里单变量求导,其实不算梯度),求偏导如下:
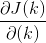
然后迭代,迭代时有个步长alpha,(深度学习中貌似叫学习率)
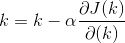
3.例子
假如我们得到样本(1,1),(2,2),(3,3).其实,由这三个样本可以得到函数为y = 1*x。此时损失函数为0.而机器是不知道的,所以我们需要训练。
下面是一段python代码。
import numpy as np import matplotlib.pyplot as plt x=np.arange(-5, 5, 0.001) y=(((x-1)*(x-1)+(x*2-2)*(x*2-2)+(x*3-3)*(x*3-3))*1/6.0) plt.plot(x,y) #plt.show() #显示图形 def sum(x): return ((x*1-1)*1+(x*2-2)*2+(x*3-3)*3) def fun(x): return ((1/3.0)*sum(x)) old = 0 new = 5 step = 0.01 pre = 0.00000001 def src_fun(x): print(((x-1)*(x-1)+(x*2-2)*(x*2-2)+(x*3-3)*(x*3-3))*1/6.0) while abs(new-old)>pre: old = new #src_fun(old) #输出每次迭代的损失值 new = new - step*fun(old) print(new) print(src_fun(new))
下图是损失函数的图像,损失函数中变量是k。下图横坐标为k的不同取值,纵轴为对应的损失大小。由下图可以大致看出,当k为1时,损失函数值为0。注意:这里取的最优值k=1是在我们已有样本的情况下得出的,样本不同,k值自然不同。
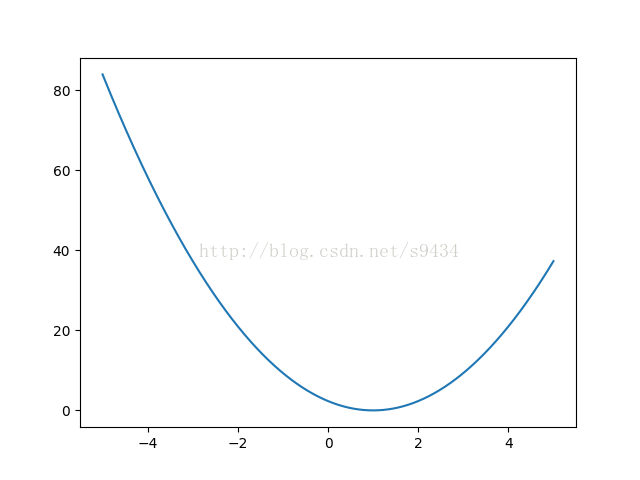
下面是print(new)和print(src_fun(new))的输出结果
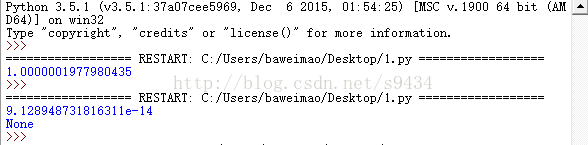
上述就是小编为大家分享的使用python怎么实现梯度下降法了,如果刚好有类似的疑惑,不妨参照上述分析进行理解。如果想知道更多相关知识,欢迎关注亿速云行业资讯频道。
免责声明:本站发布的内容(图片、视频和文字)以原创、转载和分享为主,文章观点不代表本网站立场,如果涉及侵权请联系站长邮箱:is@yisu.com进行举报,并提供相关证据,一经查实,将立刻删除涉嫌侵权内容。