C语言高效实现向量循环移位

发布时间：2020-10-21 23:40:01 作者：随心随意随缘
来源：脚本之家阅读：170

问题：n个元素的向量V循环移位（以左移为例）i个位置，例如12345循环移动2个位置得到34512.

问题本身非常简单，以至于我们一看到问题就能想到对应的解决策略：申请i个字节的动态存储，将向量区间[0,i-1]的i个元素存储至临时存储器，之后将[i,n]的n-i+1个元素向左移动i个位置，并将临时存储器中的i个元素写回原向量区间中[n-i+1,n]。但如果我们强加一些限制：在现有可申请内存的总量k << i以及所要求的时间复杂度为O(n)的情况下如何实现循环移位？问题的复杂度似乎就上了一个量级。而之所以写这篇文章，很大程度上是因为接下来要介绍的三种方法带来了对问题本质更深入的思考。

方法一(姑且称之为求模法)：借助一个临时变量temp，temp ← V[0]，V[0] ← V[i%n]，V[i%n] ← V[(2i)%n]…直到(ki)%n =0时，此时所要完成的操作即为V[((k-1)i)%n] ← V[0]，而由于变量V[0]的值在被V[i%n]覆盖之前已存入temp，取而代之的操作即为：V[((k-1)i)%n] ← temp。图解表示为(图示的移位个数为i=3)：

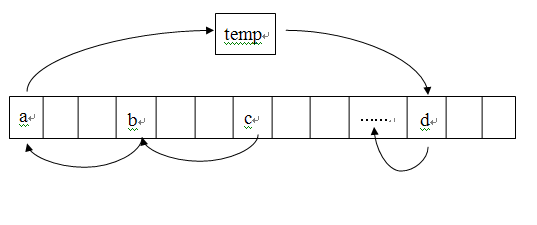
C语言高效实现向量循环移位

整个操作过程借助一个临时变量，经过n次左右的操作即完成整个移位过程，时间复杂度满足O(n)。事实上，向量中所有的元素都进行了移位操作，因此如果当完成V[((k-1)i)%n] ← temp操作时，仍有元素未完成移动，此时从V[1]开始再次进行移动。因为如果没有移动全部的元素，则说明最初的i个元素将分为m(m>1)个等价类，所以从V[1]开始再次移动是可行的，这归功于等价类的性质：任何求模等价类聚集中每个集合中的每个元素间隔的长度相等。所以若0和1同属一个等价类，则该等价类必然包含所有i个元素。

上述过程的伪码表示为：

/*LOOPSHIFT(V,i)*/
cnt←0
j←-1
while cnt≠length[V]
 do j←j+1
   temp←V[j]
   k←i+j
   while k%n≠j
    do V[(k-i)%n]←V[k%n]
     k←k+i
     cnt←cnt+1
   V[(k-i)%n]←temp
   cnt←cnt+1

在继续深入考虑之前先思考以下两种情况：①在13个元素中循环移动5个元素(12/5) ②在14个元素中移动4个元素(14/4)，其中⌈⌉表示上取整，⌊⌋表示下取整。

1)在13/5这种情况中，由于(⌈12/5⌉)×5-12=3，每次在5个元素中以2进行循环迭代，在[0,4]这5个元素中的迭代次序为(不考虑向量中的其他元素)：0→3→1(6%5)→4(9%5)→2(12%5)→0(15%5)，因此最终通过上述代码的一次内层循环即可完成整个移位操作。

2)在14/4这种情况中，由于(⌈14/4⌉)×4-14=2，每次在4个元素中也以2进行循环迭代，在[0,3]这5个元素中的迭代次序为：0→2→0(4%2)→1(退出内层循环，简单从下标为1的元素重新开始移动)→3→1(5%2)，因此最后在外层执行两次迭代才最终完成整个移位操作。

通过这两个例子可以发现外层的迭代次数(即等价类的个数)最终和整个向量的长度以及所要移位的个数有关，具体的关系为：cnt = gcd(n,i) 其中n=length[A]，cnt为外层迭代的次数。

由于任何求模等价类聚集中每个集合中的元素间隔的长度相等(由上可知，即实际过程中未进行模运算之前的值)，据此证明过程如下：

因为length[V]=n且移位个数为i，因此必然存在大于等于n且被i整除的数k=⌈n/i⌉×i

由n= α×gcd(n,i)且i=β×gcd(n,i)，k=⌈n/i⌉×β×gcd(n,i)

因此在i个元素上每次移位的个数为iter=k-n=(⌈n/i⌉×β-α)×gcd(n,i)，即iter能被gcd(n,i)整除

由于对元素求模各等价类的个数即为等价类中每个元素的间隔长度，因此实际在i个元素中进行iter个移位所得的等价类即为：

i×iter/lcm(n,i)=gcd(i,iter)=gcd(i,(⌈n/i⌉×β-α)×gcd(n,i))，由于i=β×gcd(n,i)可得gcd(β,⌈n/i⌉×β-α)=1

由此可知gcd(i,iter)=gcd(n,i)，因此结论得证，共有cnt=gcd(n,i)个等价类，每个等价类的代表所构成的集合为{0,1,…,cnt-1}（用近世代数的术语来说，也就是旋转产生的置换群的陪集个数）。

因此上述伪码可重写为：

/*LOOPSHIFT(V,i) --gcd version*/
for cnt←0 to gcd(n,i)-1    /*n=length[V], "cnt←0 to n"means assign cnt in [0,n] */
 do temp←V[cnt]
   k←i
   for j←1 to (length[V]/gcd(n,i))-1
    do V[(k-i)%n]←V[k%n]
     k←k+i
   V[(k-i)%n]←temp

第二种方法(递归法)：令V=ab(a为要移位的个数，length[a]与length[b]不一定相等)，则旋转向量V实际就是交换向量ab得到ba，假定length[a]<length[b]，分解向量b=αβ，使得length[a]=length[β]，同样借助一个临时变量temp可实现向量a和β的交换，可得到第一次迭代之后的向量为βαa，接下来在对βα向量执行同样地交换，执行一系列交换之后最终得到向量ba，而递归最终到达不动点(fix-point)的条件即为所要交换的两个向量长度相等，即移位值为0。实际就是将原问题分解为一系列性质类似的子问题，利用分治的思想逐个击破，最终达到整体交换的目标。

以上方法的伪码实现为：

/*LOOPSHIFT(V,i) --recurrence version*/
//RECSHIFT(V, i, low, high)   /*low:lower_bound high:higher_bound*/
if low=high || high<i      /*i is a fix value*/
 then return            
if i-low>high-i+1         /*select a min value as the count of reversion*/
 then revcnt←high-i+1
    flag←1          /*set the flag value low bound increase*/
 else revcnt←i-low
for j←0 to revcnt-1  /*swap the elem in the vector i times*/
 do temp←V[low+j] 
   V[low+j]←V[high+1+j-revcnt]
   V[high+1+j-revcnt]←temp
if flag=1
 then low←low+revcnt
 else high←high-revcnt
RECSHIFT(V,i,low,high)  /*call itself*/

第三种方法(求逆法)：令V=ab(其中a为要移位的个数)，①对向量V中的前a个元素做求逆操作得到V'=a'b；②对向量V中的接下来的b个元素做求逆操作得到V''=a'b'；③对整个向量V做求逆操作得到V'''=(a'b')'=ba。(同阶方阵A，B有(AB)'=B'A')为了验证该操作是否可行，以文章开始处所举的例子(12345循环移动2个位置)进行求逆操作：12345→(①)21345→(②)21543→(③)34512，结果成立，说明该操作可行。而求逆操作中所包含的思想其实很简单：我们在观察一个字符串的时候往往是从左往右看的，而要循环移动其中i位，实际是将这i个字符放在整个串的末尾。而如果我们从右往左看呢？我们发现其实原本在字符串中的长度为i的子串到了整个串的末尾(即54321)，我们发现两个子串的长度换好了，但是每个子串是逆序排列的，这个时候对两个子串各做一次求逆操作不就得出了最终的结果了吗？这种方法所带来的思考是：实际解决一个问题的时候，如果发现考虑的思路遇到较大阻碍，换个视角看问题往往能有意想不到的效果。

以上方法的伪码实现为：

/*LOOPSHIFT(V,i) --reverse version*/
//REVERSE(V,i,high)    /*high=high_bound*/
REVERSE(V,0,i-1)
REVERSE(V,i,high)
REVERSE(V,0,high)
//--------------------------------------------------
REVERSE(V,low,high) /*function body*/
for j←0 to ((high-low+1)/2)-1
 do temp←V[low+j]
   V[low+j]←V[high-j]
   V[high-j]←temp

ps:对于第三种方法，著名计算机科学家，unix以及C语言前身B语言的设计者Ken•Thompson在编辑器中使用这种求逆代码时就主张将该代码作为一种常识。

至此三种方法都介绍完了，细心的读者也许发现前两种方法只进行了n次交换操作，而第三种方法进行了2n次操作，因此第三种方法的性能从运行时间的角度来看应该是三种方法中最差的，理论上是如此，多进行操作的算法往往耗时也越长，但实际呢？我们不妨做个试验来验证一下，为了更加真实的模拟现实，n和i的取值分别如下：

n=10000000,i={21,22,…,100}，分别对移位个数在[21,100]之间进行总运行时间的测量，测试代码如下(具备可移植性，在win/linux上均可运行，其中win_xp和linux/ubuntu在本机上测试成功得出相应数据，win_7下的版本在同学的系统上运行得出相应数据)：

//#define __LINUX__
#define __WINDOWS__
 
#include <stdio.h>
#ifdef __WINDOWS__
#include <memory.h>
#include <Windows.h>
#endif
#ifdef __LINUX__
#include <string.h>
#include <sys/time.h>
#include <unistd.h>
#endif
 
#define cntoffun          3
#define cntofi              80
#define start              20
 
#ifdef __WINDOWS__
#define mintomillsec        (60*1000)
#define sectomillsec        1000
#endif
#ifdef __LINUX__
#define sectomicrosec      (1e6)
#define microsectomillisec  (1e-3)
#define startp              0
#define endp              1
#endif
 
/*i from 21 to 100*/
#define v_length            10000000
char vec[v_length];
 
int gcd(int n, int i);
void swap(char *a,char *b);
void loopshift_gcd(char v[],int i,int high);
void recshift(char v[],int i,int low,int high);
void reverse(char v[],int low,int high);
void reverseshift(char v[],int i,int high);
typedef int DWORD;
 
int main()
{
#ifdef __WINDOWS__
 SYSTEMTIME tm;
#endif
#ifdef __LINUX__
 struct timeval tv[2];
#endif
 
 char colofline[]="yrb";
 DWORD s_millsec,e_millsec;
 FILE *fp;
 int i,j;
 size_t timearray[cntoffun][cntofi];
 memset(vec,0,sizeof(vec));
 memset(timearray,0,sizeof(timearray));
 
#ifdef __WINDOWS__
 fp=fopen("F:\\gettimeofrp.m","w");
#endif
#ifdef __LINUX__
 fp=fopen("/home/raine/Desktop/gettimeofrp.m","w");
#endif
 
 for(j=0;j<cntoffun;j++)
 {
 for(i=start+1;i<=(start+cntofi);i++)
 {
  printf("func[%d]\tcount_of_shift[%d]\t",j,i);
#ifdef __WINDOWS__
  GetLocalTime(&tm);
  s_millsec=tm.wMinute*mintomillsec+tm.wSecond*sectomillsec+ \
                    tm.wMilliseconds;
#endif
#ifdef __LINUX__
  gettimeofday(&tv[startp],NULL);
#endif
 
  if (j==0)
  loopshift_gcd(vec,i,v_length-1);
  else if (j==1)
  recshift(vec,i,0,v_length-1);
  else
  reverseshift(vec,i,v_length-1);
  
#ifdef __WINDOWS__
  GetLocalTime(&tm);
  e_millsec=tm.wMinute*mintomillsec+tm.wSecond*sectomillsec+ \
                    tm.wMilliseconds;
  timearray[j][i-start-1] = e_millsec - s_millsec;
#endif
#ifdef __LINUX__
  gettimeofday(&tv[endp],NULL);
  timearray[j][i-start-1] = ((tv[endp].tv_sec-tv[startp].tv_sec)*sectomicrosec+\
                  (tv[endp].tv_usec-tv[startp].tv_usec))*microsectomillisec; 
#endif
  printf("use time %d\n",timearray[j][i-start-1]);
 }
 }
 
 /*matlab code*/
 fprintf(fp,"clear;\nclc;\nord_x=[...\n");
 for(i=start+1;i<=(start+cntofi);i++)
 {
 fprintf(fp,"%d ",i);
 if(i%10==0) fprintf(fp,"...\n");
 }
 fprintf(fp,"];\n\n");
 for(i=0;i<cntoffun;i++)
 { 
 fprintf(fp,"ord_yfunc%d=[...\n",i+1);
 for(j=0;j<cntofi;j++)
 {
  fprintf(fp,"%d ",timearray[i][j]);
  if ((j+1)%10 == 0) fprintf(fp,"...\n");
 }
 fprintf(fp,"];\n\n");
 }
 fprintf(fp,"title('performance of three function');\n");
 fprintf(fp,"xlabel('x=[21:100]');\n");
 fprintf(fp,"ylabel('the time three function use(millisecond)');\n");
 fprintf(fp,"hold on;\n");
 for(i=0;i<cntoffun;i++)
 fprintf(fp,"plot(ord_x,ord_yfunc%d,'%c*-');\n",i+1,colofline[i]);
 fprintf(fp,"legend('func1'");
 for(i=1;i<cntoffun;i++)
 fprintf(fp,",'func%d'",i+1);
 fprintf(fp,");");
 fclose(fp);
 
 printf("\nhave been finished,press any key to quit ^ ^\n");
#ifdef __WINDOWS__
 system("pause");
#endif
}
 
void swap(char *a,char *b)
{
 char temp=*a;*a=*b;*b=temp;
}
 
int gcd(int n,int i) /*n:length[v], i:shift times, n>=i*/
{
 int temp=i;
 while(n%i != 0)
 {
 temp = n%i;
 n=i; i=temp;
 }
 return temp;
}
 
void loopshift_gcd(char v[],int i,int high)
{
 size_t length = gcd(high+1,i);
 size_t cntofelem = ((high+1)/length)-1;
 int cnt, j, k;
 char temp;
 for(cnt=0;cnt<length;cnt++)
 {
 temp=v[cnt];
 k=i;
 for(j=1;j<=cntofelem;j++)
 {
  v[(k-i)%(high+1)] = v[k%(high+1)];
  k+=i;
 }
 v[(k-i)%(high+1)]=temp;
 }
}
 
void recshift(char v[],int i,int low,int high)
{
 int revcnt,j,temp=0;
 if(low == high || high<i) return;
 
 if (i-low>high-i+1)
 revcnt=high-i+1,temp=1;
 else
 revcnt=i-low;
 for(j=0;j<=revcnt-1;j++)
 swap(&v[low+j],&v[high+1+j-revcnt]);
 if(temp == 1)
 low+=revcnt;
 else
 high-=revcnt;
 recshift(v,i,low,high);
}
 
void reverse(char v[],int low,int high)
{
 int j;
 for(j=0;j<(high-low+1)/2;j++)
 swap(&v[low+j],&v[high-j]);
}
 
void reverseshift(char v[],int i,int high)
{
 reverse(v,0,i-1);
 reverse(v,i,high);
 reverse(v,0,high);
}

结果运行之后所得到的M文件(matlab)如下(只展示了xp下所得出的版本)：

%win_xp version
clear;
clc;
ord_x=[...
21 22 23 24 25 26 27 28 29 30 ...
31 32 33 34 35 36 37 38 39 40 ...
41 42 43 44 45 46 47 48 49 50 ...
51 52 53 54 55 56 57 58 59 60 ...
61 62 63 64 65 66 67 68 69 70 ...
71 72 73 74 75 76 77 78 79 80 ...
81 82 83 84 85 86 87 88 89 90 ...
91 92 93 94 95 96 97 98 99 100 ...
];
 
ord_yfunc1=[...
187 157 156 141 156 156 172 187 172 187 ...
204 187 203 219 203 219 219 250 234 234 ...
250 250 266 266 265 281 266 297 281 297 ...
313 312 313 328 312 344 359 360 359 359 ...
375 360 375 375 375 390 391 391 390 391 ...
391 406 390 407 422 406 406 391 406 406 ...
391 422 407 421 422 469 469 422 484 484 ...
422 407 437 422 422 437 453 485 500 453 ...
];
 
ord_yfunc2=[...
16 15 16 15 16 16 15 16 16 15 ...
16 31 16 15 0 0 0 0 31 0 ...
16 16 15 16 16 15 16 15 16 16 ...
15 16 16 15 16 15 16 16 15 16 ...
16 15 16 31 16 15 16 15 16 15 ...
32 15 16 16 15 15 16 16 15 16 ...
15 16 15 16 16 15 16 16 15 15 ...
16 16 15 16 16 15 16 15 16 16 ...
];
 
ord_yfunc3=[...
16 16 15 16 15 16 16 15 16 16 ...
15 15 16 16 15 16 16 15 16 15 ...
32 15 16 16 15 16 15 16 15 16 ...
16 15 16 15 16 16 15 16 16 31 ...
15 16 16 15 16 16 15 16 15 16 ...
31 16 16 15 16 15 16 15 16 16 ...
15 16 16 16 15 16 16 15 16 31 ...
16 15 16 16 15 16 15 16 16 31 ...
];
 
title('performance of three function(Win xp)');
xlabel('x=[21:100]');
ylabel('the time three function use(millisecond)');
hold on;
plot(ord_x,ord_yfunc1,'y*-');
plot(ord_x,ord_yfunc2,'r*-');
plot(ord_x,ord_yfunc3,'b*-');
legend('func1','func2','func3');

执行所得图形化表示如下（顺序分别为win_xp，win_7，GUN/Linux_Ubuntu）：

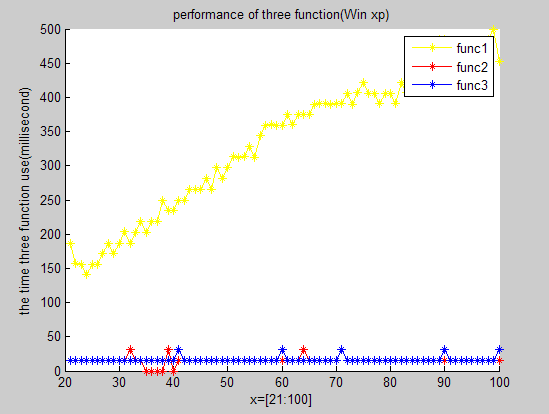
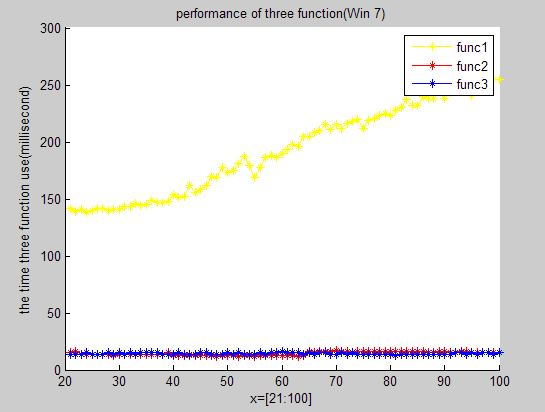
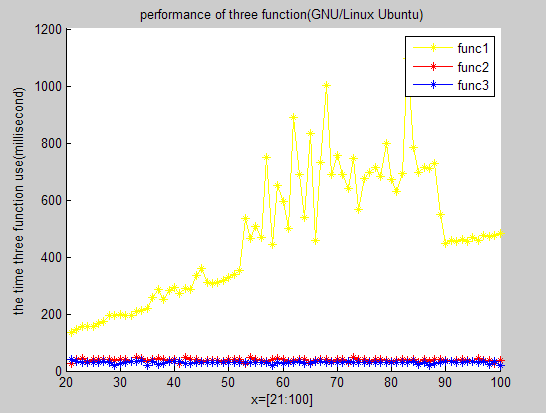
C语言高效实现向量循环移位