java编程无向图结构的存储及DFS操作代码的示例分析

这篇文章将为大家详细讲解有关java编程无向图结构的存储及DFS操作代码的示例分析，小编觉得挺实用的，因此分享给大家做个参考，希望大家阅读完这篇文章后可以有所收获。

图的概念

图是算法中是树的拓展，树是从上向下的数据结构，结点都有一个父结点（根结点除外），从上向下排列。而图没有了父子结点的概念，图中的结点都是平等关系，结果更加复杂。

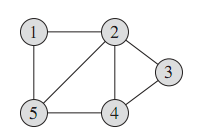
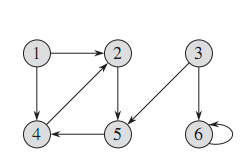
无向图                                                       有向图

图G=(V,E)，其中V代表顶点Vertex，E代表边edge，一条边就是一个定点对(u,v)，其中(u,v)∈V。

这两天遇到一个关于图的算法，在网上找了很久没有找到java版的关于数据结构中图的存储及其相关操作。于是找了一本java版的数据结构书看了一下，以下是根据书上的讲解整理的一个关于无向图的存储和对图的深度优先遍历。不过这个遍历只能遍历连通图，要想遍历非连通图，还需要修改。在这里分享一下代码希望对有需要的人有帮助。

package com.homework;
/** 
 * 定义栈类 
 */
class StackX{
	private final int size = 20;
	private int[] st;
	private int top;
	//初始化栈 
	public StackX(){
		st = new int[size];
		top = -1;
	}
	//进栈 
	public void push(int j){
		st[++top] = j;
	}
	//出栈 
	public int pop(){
		return st[top--];
	}
	//返回栈顶元素 
	public int peak(){
		return st[top];
	}
	//判断栈是否为空 
	public Boolean isEmpty(){
		return (top==-1);
	}
}
/** 
 * 定义图中的节点类 
 * @author Administrator 
 * 
 */
class Vertex{
	public char label;
	public Boolean wasVisited;
	public Vertex(char lab){
		label = lab;
		wasVisited = false;
	}
}
/** 
 * 定义图类 
 * @author Administrator 
 * 
 */
class Graph{
	private final int num = 20;
	private Vertex vertexList[];
	//图中节点数组 
	private int adjMat[][];
	//节点矩阵 
	private int nVerts;
	//当前节点数 
	private StackX theStack;
	//定义一个栈 
	//初始化图的结构 
	public Graph(){
		vertexList = new Vertex[num];
		adjMat = new int[num][num];
		nVerts = 0;
		for (int i=0; i<num; i++){
			for (int j=0; j<num; j++) 
			        adjMat[i][j] = 0;
		}
	}
	//添加节点 
	public void addVertex(char lab){
		vertexList[nVerts++] = new Vertex(lab);
	}
	//添加某两个节点之间的边 
	public void addEdge(int start,int end){
		adjMat[start][end] = 1;
		adjMat[end][start] = 1;
	}
	//输出某个节点 
	public void displayVertex(int v){
		System.out.print(vertexList[v].label);
	}
	//获取未被访问的几点 
	public int getAdjUnvisitedVertex(int v){
		for (int j=0; j<nVerts; j++){
			if(adjMat[v][j]==1 && vertexList[j].wasVisited==false) 
			        return j;
		}
		return -1;
	}
	//深度优先遍历（DFS） 
	public void dfs(){
		vertexList[0].wasVisited=true;
		displayVertex(0);
		theStack= new StackX();
		theStack.push(0);
		while(!theStack.isEmpty()){
			int v = getAdjUnvisitedVertex(theStack.peak());
			if(v==-1)//若不存在该节点 
			theStack.pop(); else 
			      {
				vertexList[v].wasVisited = true;
				displayVertex(v);
				theStack.push(v);
			}
		}
		for (int j=0; j<nVerts; j++) 
		      vertexList[j].wasVisited = false;
	}
}
public class GraphConnect {
	public static void main(String[] args){
		{
			Graph theGraph = new Graph();
			theGraph.addVertex('A');
			theGraph.addVertex('B');
			theGraph.addVertex('C');
			theGraph.addVertex('D');
			theGraph.addVertex('E');
			theGraph.addEdge(0, 1);
			//AB 
			theGraph.addEdge(1, 2);
			//BC 
			theGraph.addEdge(0, 3);
			//AD 
			theGraph.addEdge(3, 4);
			//DE 
			theGraph.addEdge(2, 4);
			//CE 
			System.out.print("The order visited:");
			theGraph.dfs();
			System.out.println();
		}
	}
}

程序运行的结果：

The order visited:ABCED

关于“java编程无向图结构的存储及DFS操作代码的示例分析”这篇文章就分享到这里了，希望以上内容可以对大家有一定的帮助，使各位可以学到更多知识，如果觉得文章不错，请把它分享出去让更多的人看到。