您好,登录后才能下订单哦!
作者——Navoneel Chakrabarty
在数据科学领域,分类问题是一个非常普遍和重要的问题。例如:糖尿病视网膜病变、情绪分析、数字识别、癌症类型预测(恶性或良性)等。这些问题往往通过机器学习或深度学习来解决。像糖尿病视网膜病变或青光眼检测这样的项目中,纹理分析经常被使用,而不是传统的图像处理或深度学习等。虽然根据研究论文,深度学习在处理糖尿病视网膜病变方面有着极强的优越性。
补充:纹理分析指通过一定的提取出纹理特征参数,从而获得纹理的定量或定性描述的处理过程·纹理分析方法按其性质而言,可分为两大类:统计分析方法和结构分析方法。纹理分析在遥感图像、 X、细胞和处理方面有广泛的应用。关于纹理,还没有一个统一的数学模型。它起源于表征纺织品表面性质的纹理概念,可以用来描述任何物质组成成分的排列情况,例如医学上X 射线照片中的、血管纹理、航天(或航空)地形照片中的岩性纹理等。图像处理中的视觉纹理通常理解为某种基本模式(色调基元)的重复排列。

现在,我们再回到主题。相关研究论文如下:
"糖尿病视网膜病变检测的深度学习方法"链接:https://ieeexplore.ieee.org/document/8596839
在分类问题中,一个特定类的预测往往要涉及多个类。换句话说,它还可以以这样一种方式构建:将特定实例(特征空间几何中的数据点)保存在特定区域下(某一类),并且与其他区域分离(其他类)。这种与其他区域的分离的"现象"我们称之为决策边界的可视化。在特征空间中决策边界的可视化是在散点图上完成的。其中每个点表示数据集的一个数据点,轴线表示特征。决策边界将数据点划分为多个区域,这些区域就是(我前面所谈及的)数据点所属的类。
决策边界的重要性/意义:
在使用数据集训练机器学习模型之后,我们通常需要可视化特征空间中数据点的类。散点图上的决策边界就是出于这个目的。而散点图更是包含着属于不同类别的数据点(用颜色或形状表示),决策边界可以通过多种不同的策略绘制:
单线决策边界:在散点图上绘制决策边界的基本策略是找到一条将数据点分隔成不同类区域的单线。现在,利用训练过的模型找到与机器学习算法相关的参数,进而找到这条直线。然后利用得到的参数和机器学习算法找到直线坐标。如果你不知道ML算法的工作原理,那么你将无法继续进行下去。
基于轮廓的决策边界:另一种策略是绘制轮廓,这些轮廓是用匹配或紧密匹配的颜色包围数据点的区域——描绘数据点所属的类,以及描绘预测类的轮廓。这是最常用的策略,因为它不使用模型训练后得到的机器学习算法的参数和相关计算。但另一方面,我们并不能很好地用一条直线来分离数据点,也就是说这条直线只能通过训练后得到的参数及其坐标计算得到。
单线决策边界的范例演练:
在这里,我将演示基于逻辑回归的机器学习模型的单线决策边界。
进入逻辑回归假设
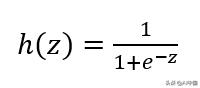
其中z被定义为:
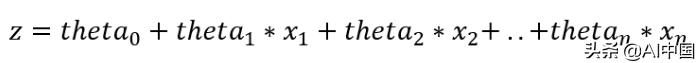
theta_1、theta_2 theta_3,....其中,theta_n为逻辑回归的参数,x_1、x_2、…、x_n为特征。
因此,h(z)是一个Sigmoid函数,其范围是从0到1(包括0和1)。
在绘制决策边界时,取h(z) = Logistic回归中使用的阈值,通常为0.5。即:
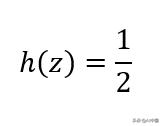
然后:
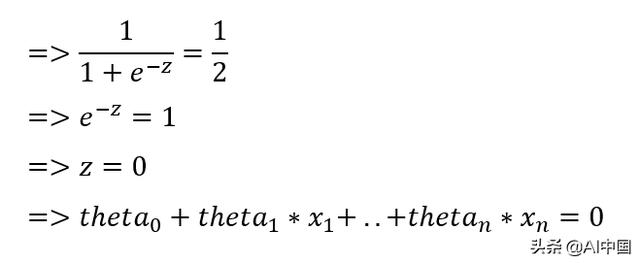
现在,在绘制决策边界时,需要考虑两个特征,并沿散点图的x轴和y轴绘制。所以,
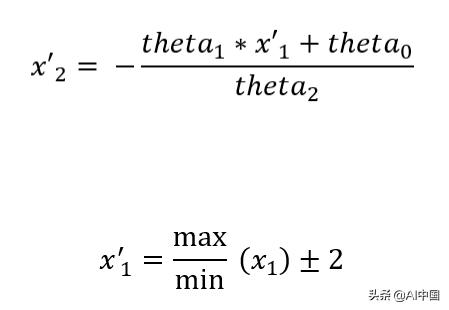
也就是说
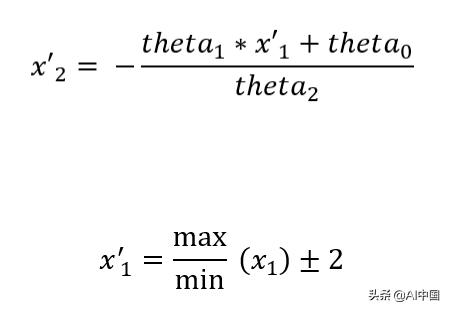
其中x_1是数据集的原始特征
因此,得到2个x ' _1的值以及2个相应的x ' _2的值。x ' _1是单线决策边界的x极值,x ' _2是单线决策边界的y极值。
在虚构数据集上的应用:
该数据集包含100名学生在2次考试中获得的分数和标签(1,0),该标签指示该学生是否将被大学录取(用1和0表示)。相关数据集链接:https://github.com/navoneel1092283/logistic_regression.git
问题陈述:"根据在两次考试中获得的分数,用逻辑回归预测该学生是否会被大学录取。"
在这里,两门考试的分数将是考虑的两个特征。
下面是具体的实现方法:
相关链接:https://hackernoon.com/logistic-regression-in-python-from-scratch-954c0196d258




对数据集进行逻辑回归:

得到(参数)向量,

获取数据点的预测或预测类:

绘制单线决策边界:




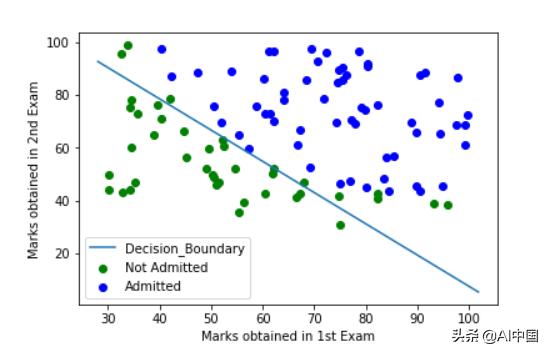
得到单线决策边界
这样,任何基于逻辑回归的机器学习模型都可以绘制出单线决策边界。对于基于其他机器学习算法的模型而言,则必须知道相应的假设等等。
基于轮廓的决策边界的范例演练:
利用刚才的数据集和训练模型,绘制基于轮廓的决策边界。


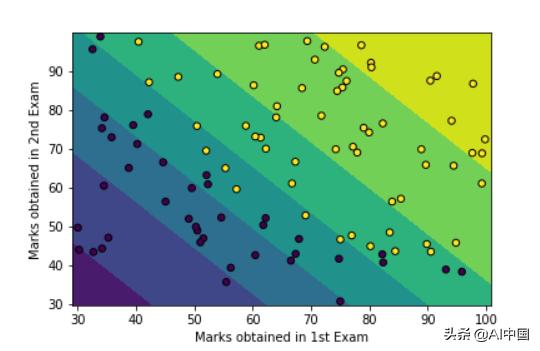
得到基于轮廓的决策边界,其中黄色->允许,蓝色->不允许
这种方法显然更方便,因为机器学习算法不需要假设,也不需要数学。所需要的只是高级Python编程的诀窍。
因此,它是绘制任意机器学习模型决策边界的一种通用方法。
在现实生活中和一些高级项目中,都会涉及到许多特征。那么,如何在二维散点图中绘制决策边界呢?
面对这种情况,我认为有多种解决办法:
1.利用随机森林分类器等给特征进行重要性评分,得到2个最重要的特征,然后在散点图上绘制决策边界。
2.主成分分析(PCA)或线性判别分析(LDA)等降维技术可用于将N个特征嵌入到2个特征中,从而将N个特征的信息解释或减少为2个特征(n_components = 2)。然后再基于这两个特征在散点图上绘制决策边界。
这就是决策边界可视化。
免责声明:本站发布的内容(图片、视频和文字)以原创、转载和分享为主,文章观点不代表本网站立场,如果涉及侵权请联系站长邮箱:is@yisu.com进行举报,并提供相关证据,一经查实,将立刻删除涉嫌侵权内容。