您好,登录后才能下订单哦!
这篇文章将为大家详细讲解有关图的广度优先遍历算法类似于二叉树的示例分析,小编觉得挺实用的,因此分享给大家做个参考,希望大家阅读完这篇文章后可以有所收获。
图的广度优先遍历即横向优先遍历,类似于二叉树的按层遍历。广度优先遍历是从根结点开始沿着树的宽度搜索遍历,即按层次的去遍历;从上往下对每一层依次访问,在每层中,从左往右(或右往左)访问结点,访问完一层就进入下一层,直到没有结点可以访问为止。
1.前言
和树的遍历类似,图的遍历也是从图中某点出发,然后按照某种方法对图中所有顶点进行访问,且仅访问一次。
但是图的遍历相对树而言要更为复杂。因为图中的任意顶点都可能与其他顶点相邻,所以在图的遍历中必须记录已被访问的顶点,避免重复访问。
根据搜索路径的不同,我们可以将遍历图的方法分为两种:广度优先搜索和深度优先搜索。
顶点对(u,v)是无序的,即(u,v)和(v,u)是同一条边。常用一对圆括号表示。
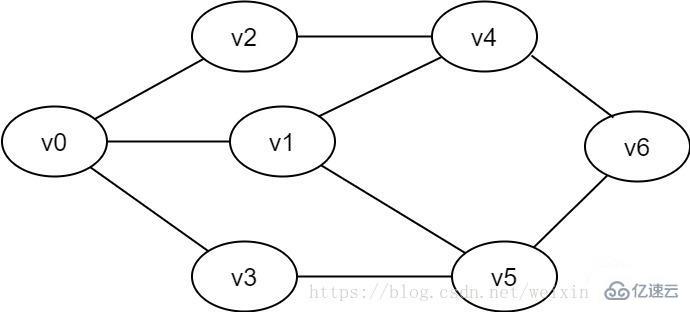
图2-1-1 无向图示例
顶点对<u,v>是有序的,它是指从顶点u到顶点 v的一条有向边。其中u是有向边的始点,v是有向边的终点。常用一对尖括号表示。
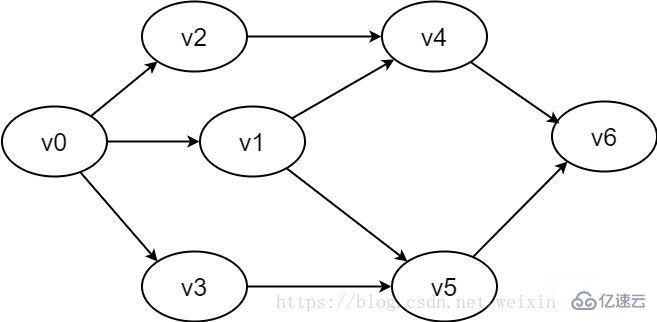
图2-1-2 有向图示例
图的每条边上可能存在具有某种含义的数值,称该数值为该边上的权。而这种带权的图被称为网。
连通图:在无向图G中,从顶点v到顶点v'有路径,则称v和v'是联通的。若图中任意两顶点v、v'∈V,v和v'之间均联通,则称G是连通图。上述两图均为连通图。
非连通图:若无向图G中,存在v和v'之间不连通,则称G是非连通图。
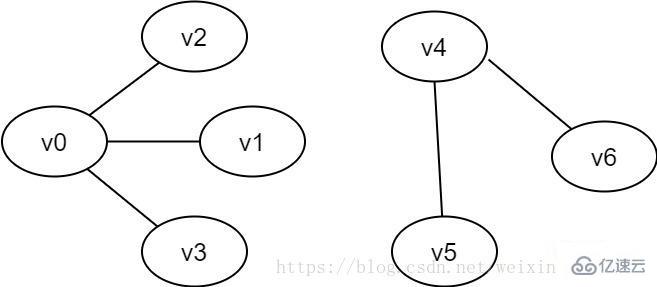
图2-3 非连通图示例
广度优先搜索类似于树的层次遍历过程。它需要借助一个队列来实现。如图2-1-1所示,要想遍历从v0到v6的每一个顶点,我们可以设v0为第一层,v1、v2、v3为第二层,v4、v5为第三层,v6为第四层,再逐个遍历每一层的每个顶点。
具体过程如下:
1.准备工作:创建一个visited数组,用来记录已被访问过的顶点;创建一个队列,用来存放每一层的顶点;初始化图G。
2.从图中的v0开始访问,将的visited[v0]数组的值设置为true,同时将v0入队。
3.只要队列不空,则重复如下操作:
(1)队头顶点u出队。
(2)依次检查u的所有邻接顶点w,若visited[w]的值为false,则访问w,并将visited[w]置为true,同时将w入队。
白色表示未被访问,灰色表示即将访问,黑色表示已访问。
visited数组:0表示未访问,1表示以访问。
队列:队头出元素,队尾进元素。
1.初始时全部顶点均未被访问,visited数组初始化为0,队列中没有元素。
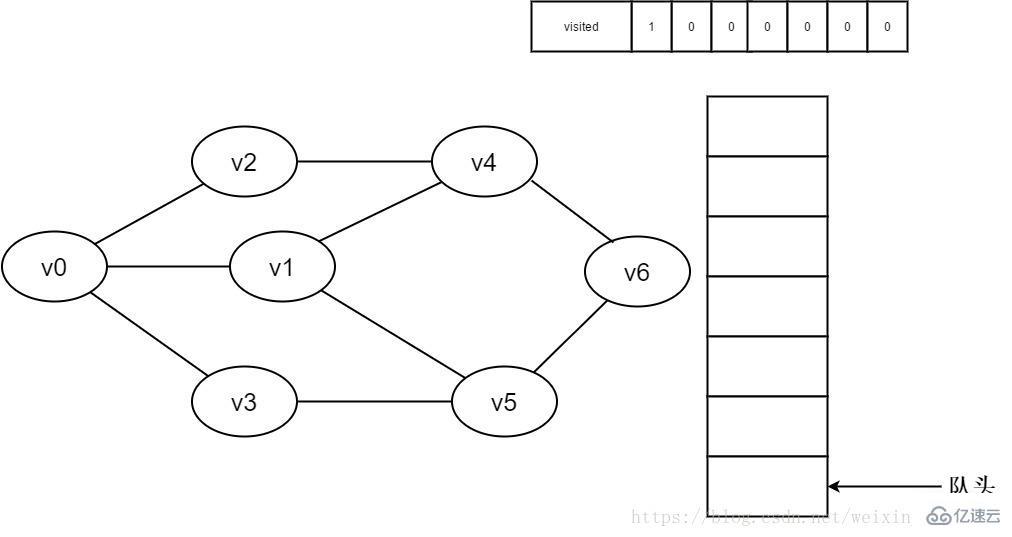
图3-2-1
2.即将访问顶点v0。
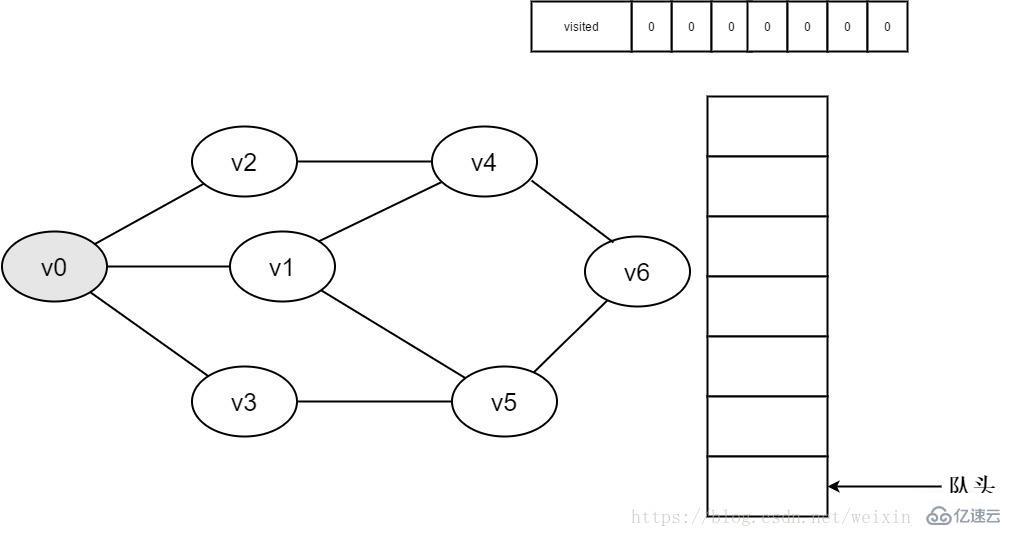
图3-2-2
3.访问顶点v0,并置visited[0]的值为1,同时将v0入队。
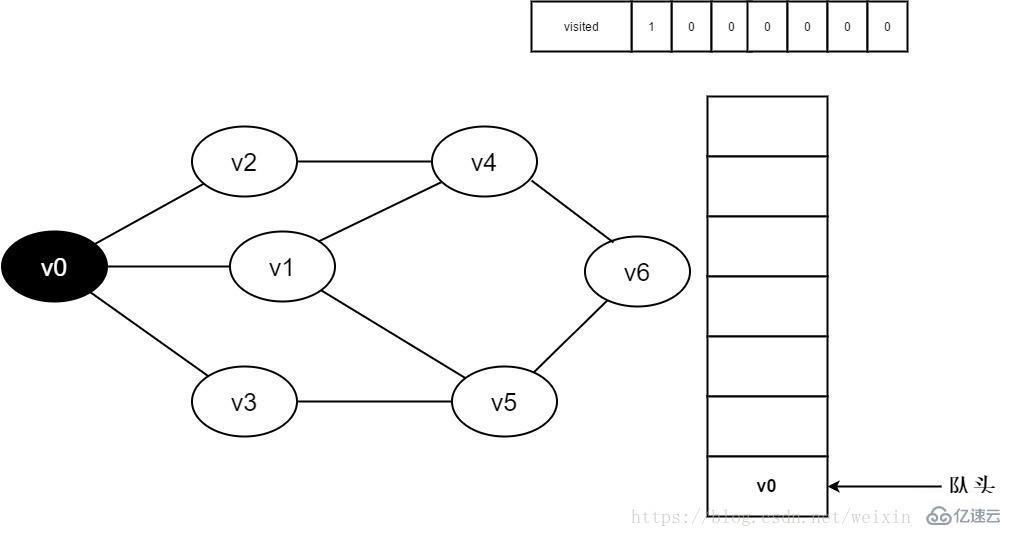
图3-2-3
4.将v0出队,访问v0的邻接点v2。判断visited[2],因为visited[2]的值为0,访问v2。
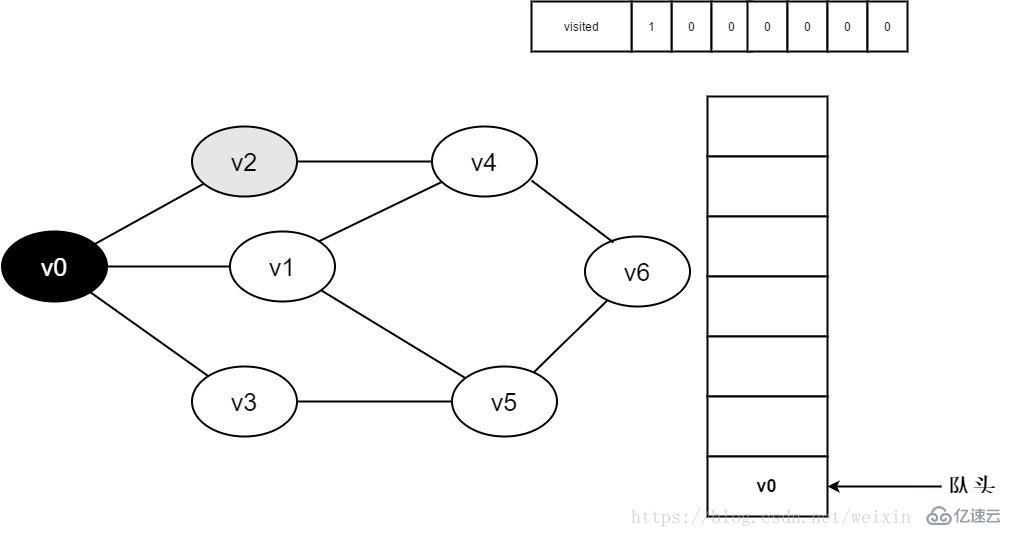
图3-2-4
5.将visited[2]置为1,并将v2入队。
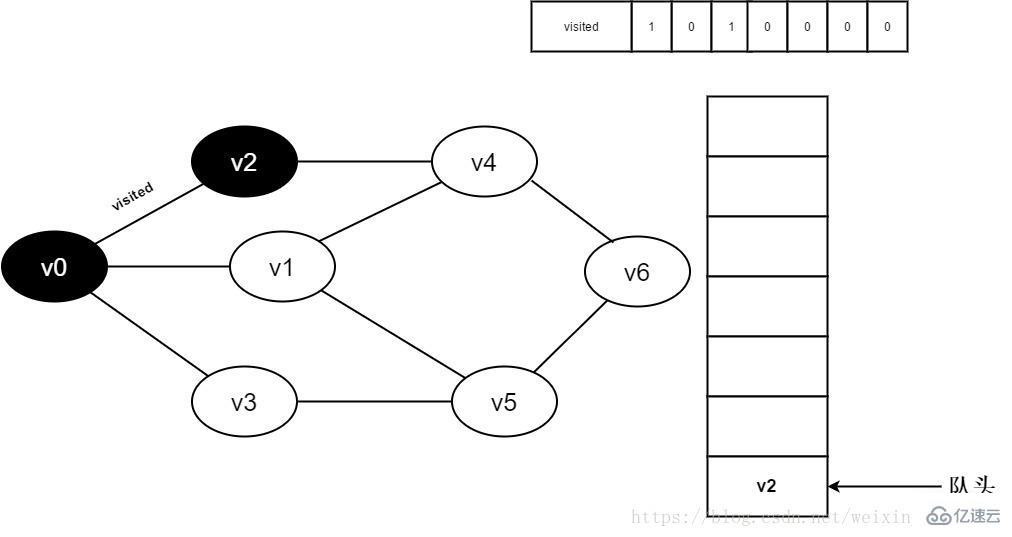
图3-2-5
6.访问v0邻接点v1。判断visited[1],因为visited[1]的值为0,访问v1。
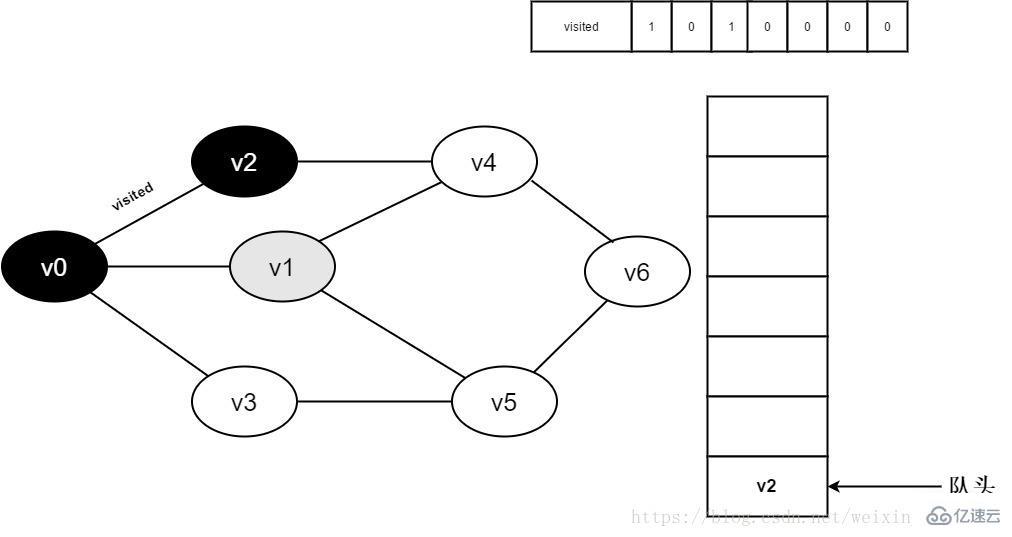
图3-2-6
7.将visited[1]置为0,并将v1入队。
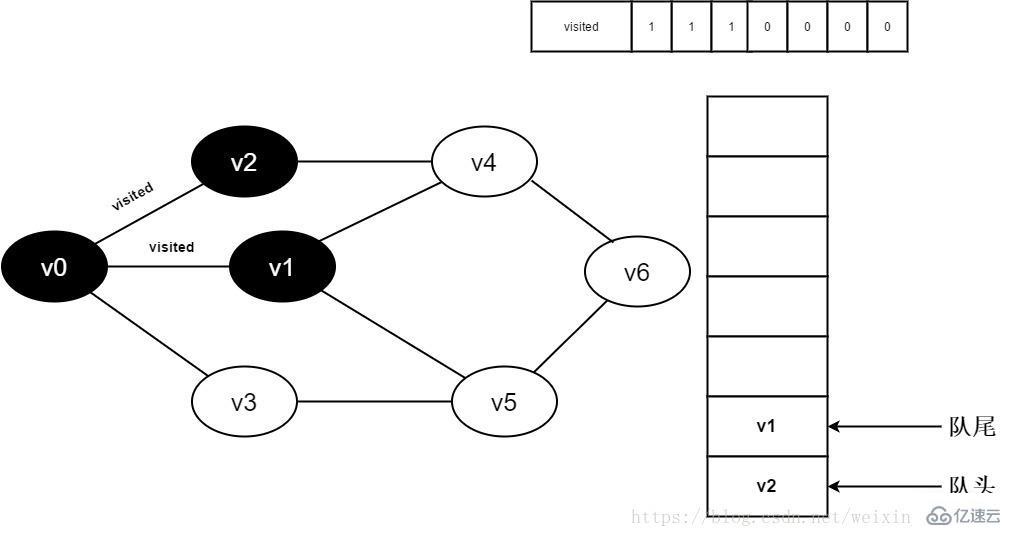
图3-2-7
8.判断visited[3],因为它的值为0,访问v3。将visited[3]置为0,并将v3入队。
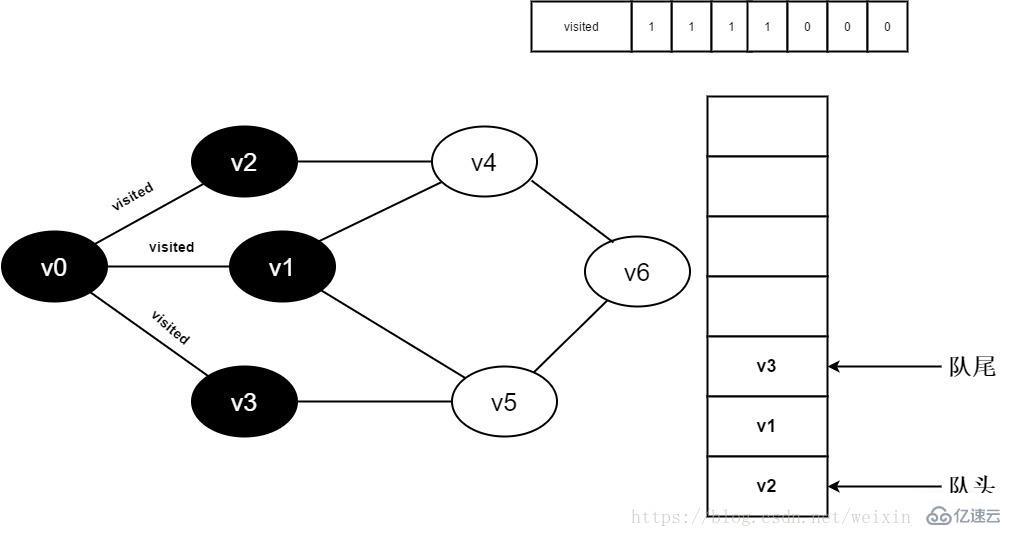
图3-2-8
9.v0的全部邻接点均已被访问完毕。将队头元素v2出队,开始访问v2的所有邻接点。
开始访问v2邻接点v0,判断visited[0],因为其值为1,不进行访问。
继续访问v2邻接点v4,判断visited[4],因为其值为0,访问v4,如下图:

图3-2-9
10.将visited[4]置为1,并将v4入队。
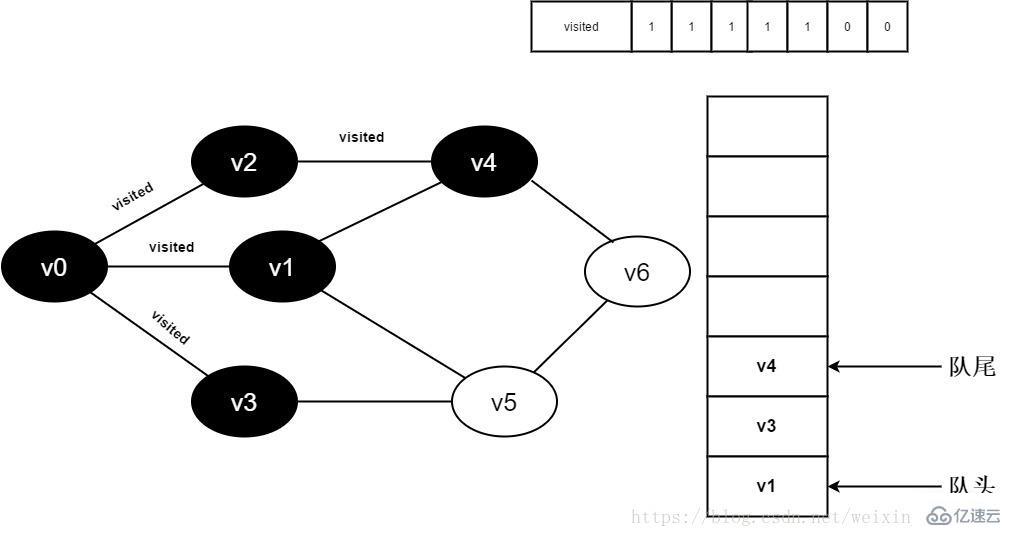
图3-2-10
11.v2的全部邻接点均已被访问完毕。将队头元素v1出队,开始访问v1的所有邻接点。
开始访问v1邻接点v0,因为visited[0]值为1,不进行访问。
继续访问v1邻接点v4,因为visited[4]的值为1,不进行访问。
继续访问v1邻接点v5,因为visited[5]值为0,访问v5,如下图:
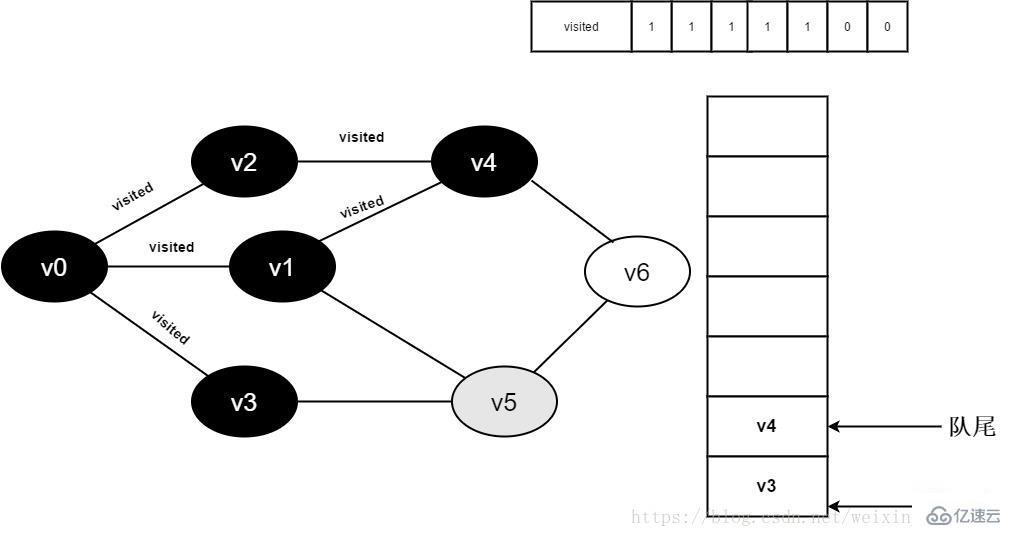
图3-2-11
12.将visited[5]置为1,并将v5入队。
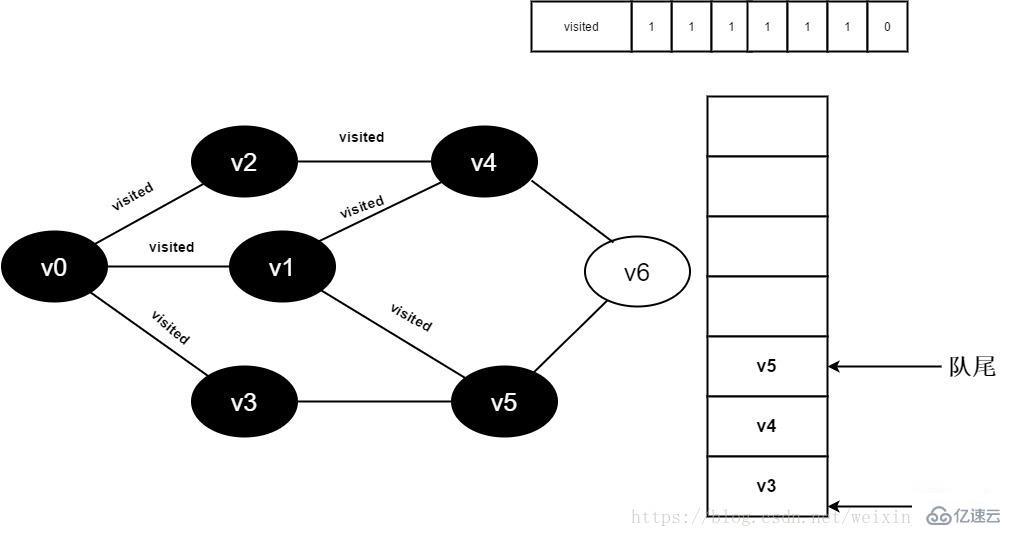
图3-2-12
13.v1的全部邻接点均已被访问完毕,将队头元素v3出队,开始访问v3的所有邻接点。
开始访问v3邻接点v0,因为visited[0]值为1,不进行访问。
继续访问v3邻接点v5,因为visited[5]值为1,不进行访问。
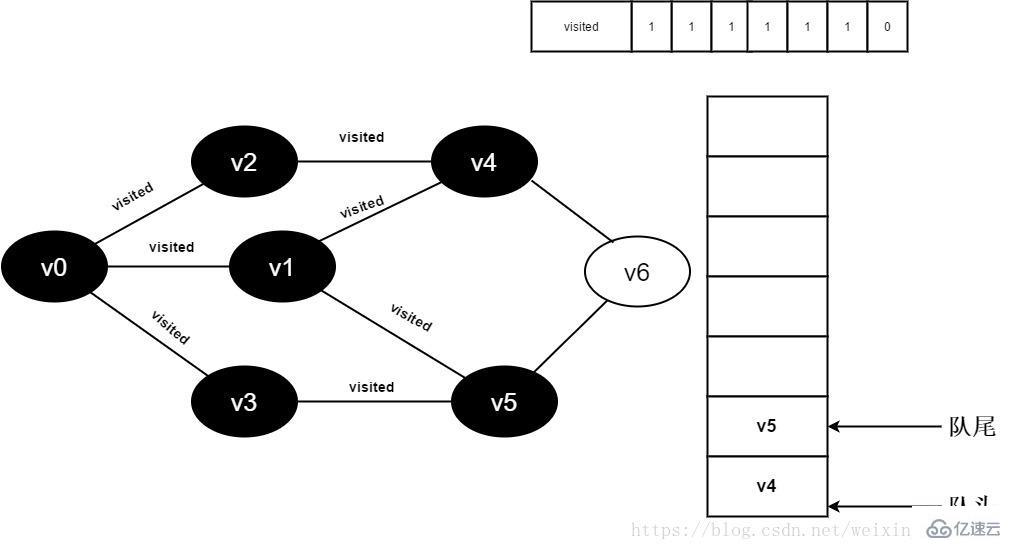
图3-2-13
14.v3的全部邻接点均已被访问完毕,将队头元素v4出队,开始访问v4的所有邻接点。
开始访问v4的邻接点v2,因为visited[2]的值为1,不进行访问。
继续访问v4的邻接点v6,因为visited[6]的值为0,访问v6,如下图:
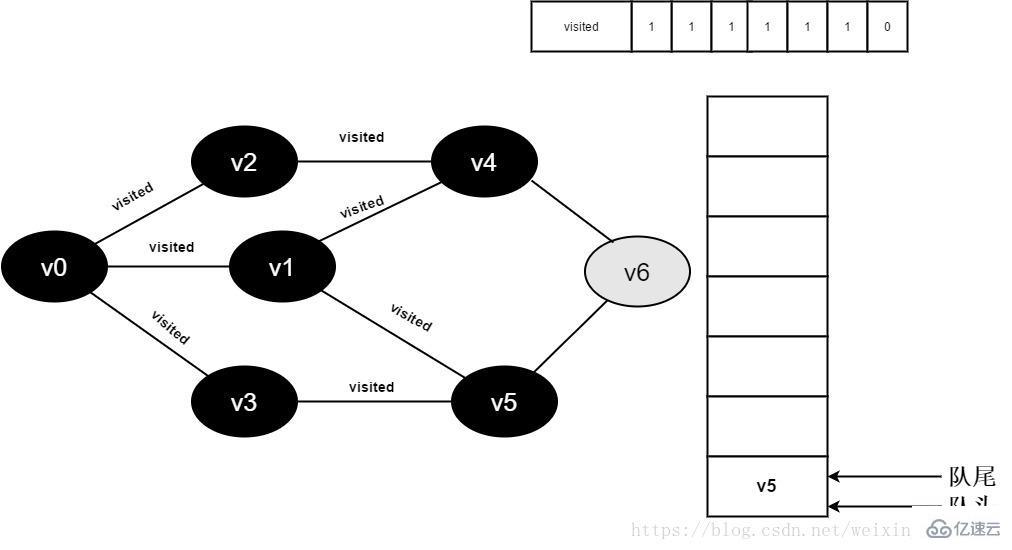
图3-2-14
15.将visited[6]值为1,并将v6入队。
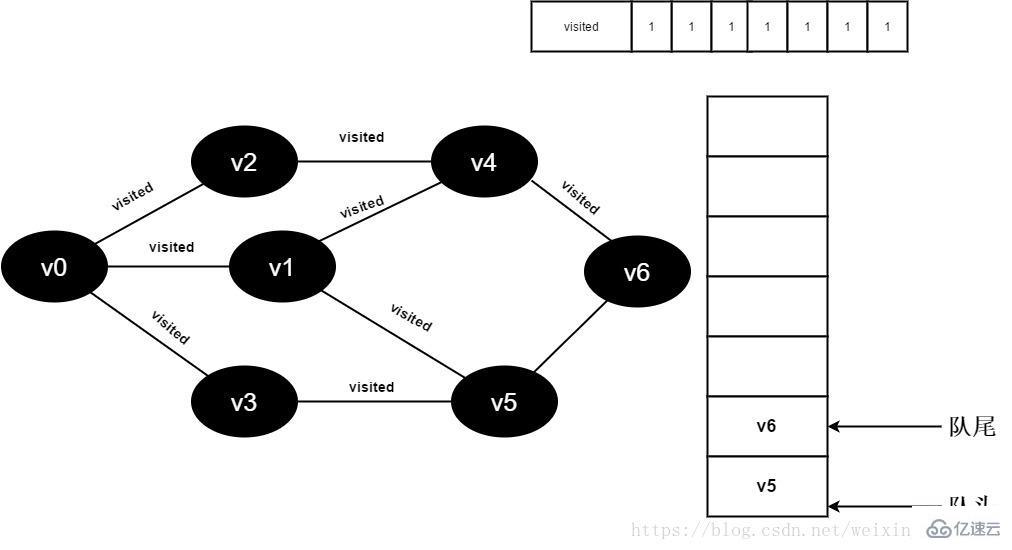
图3-2-15
16.v4的全部邻接点均已被访问完毕,将队头元素v5出队,开始访问v5的所有邻接点。
开始访问v5邻接点v3,因为visited[3]的值为1,不进行访问。
继续访问v5邻接点v6,因为visited[6]的值为1,不进行访问。
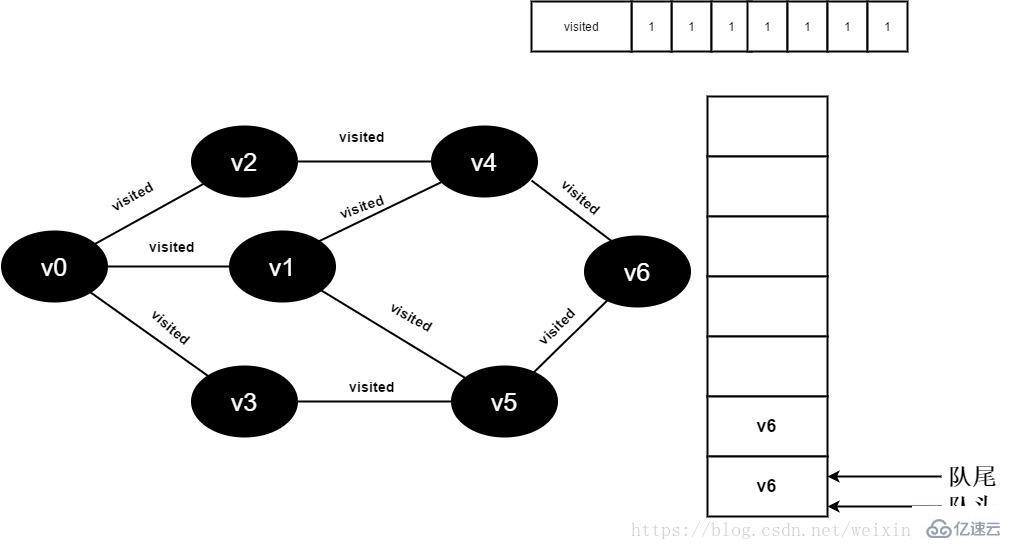
图3-2-16
17.v5的全部邻接点均已被访问完毕,将队头元素v6出队,开始访问v6的所有邻接点。
开始访问v6邻接点v4,因为visited[4]的值为1,不进行访问。
继续访问v6邻接点v5,因为visited[5]的值文1,不进行访问。
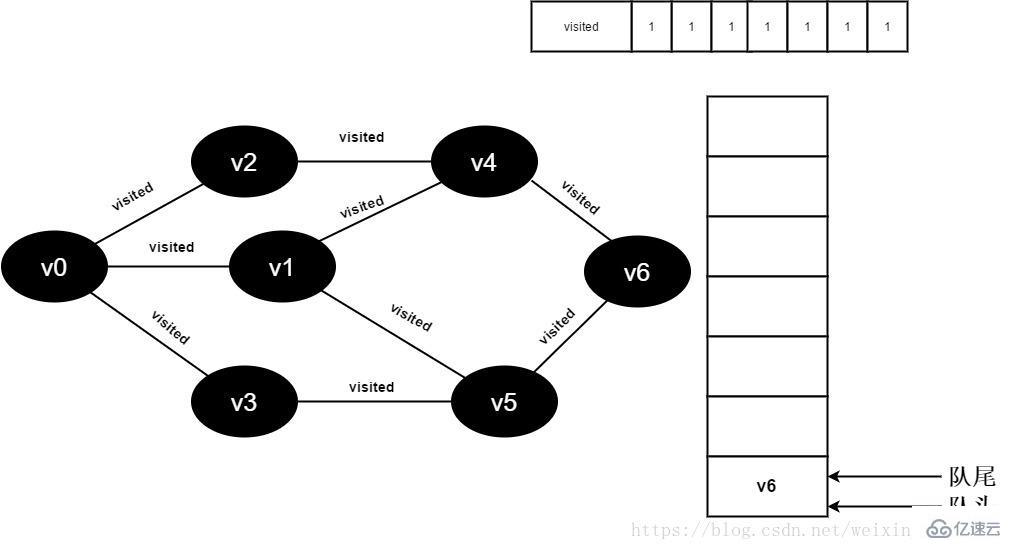
图3-2-17
18.队列为空,退出循环,全部顶点均访问完毕。
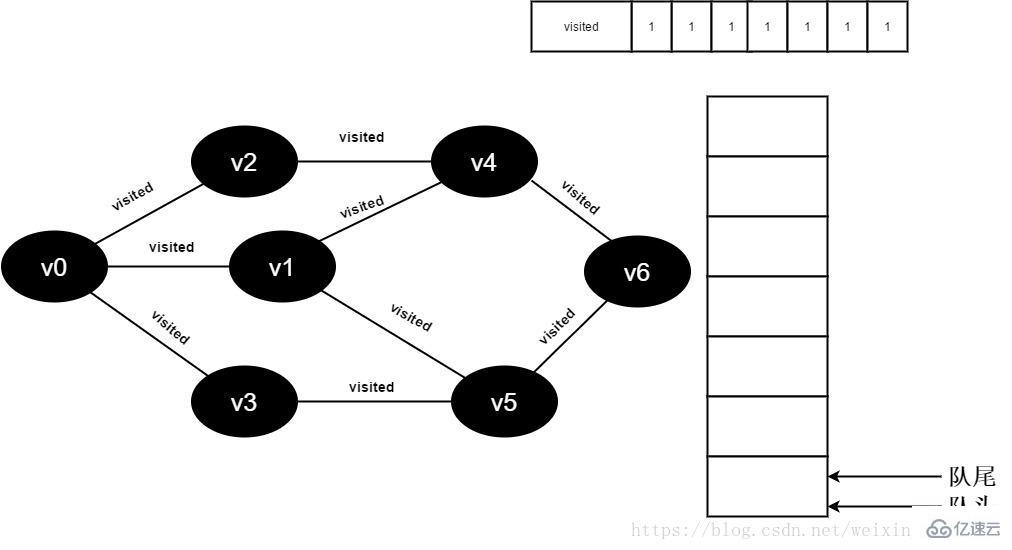
图3-2-18
/*一些量的定义*/ queue<char> q; //定义一个队列,使用库函数queue #define MVNum 100 //表示最大顶点个数 bool visited[MVNum]; //定义一个visited数组,记录已被访问的顶点
/*邻接矩阵存储表示*/
typedef struct AMGraph
{
char vexs[MVNum]; //顶点表
int arcs[MVNum][MVNum]; //邻接矩阵
int vexnum, arcnum; //当前的顶点数和边数
}
AMGraph;/*找到顶点v的对应下标*/
int LocateVex(AMGraph &G, char v)
{
int i;
for (i = 0; i < G.vexnum; i++)
if (G.vexs[i] == v)
return i;
}/*采用邻接矩阵表示法,创建无向图G*/
int CreateUDG_1(AMGraph &G)
{
int i, j, k;
char v1, v2;
scanf("%d%d", &G.vexnum, &G.arcnum); //输入总顶点数,总边数
getchar(); //获取'\n’,防止其对之后的字符输入造成影响
for (i = 0; i < G.vexnum; i++)
scanf("%c", &G.vexs[i]); //依次输入点的信息
for (i = 0; i < G.vexnum; i++)
for (j = 0; j < G.vexnum; j++)
G.arcs[i][j] = 0; //初始化邻接矩阵边,0表示顶点i和j之间无边
for (k = 0; k < G.arcnum; k++)
{
getchar();
scanf("%c%c", &v1, &v2); //输入一条边依附的顶点
i = LocateVex(G, v1); //找到顶点i的下标
j = LocateVex(G, v2); //找到顶点j的下标
G.arcs[i][j] = G.arcs[j][i] = 1; //1表示顶点i和j之间有边,无向图不区分方向
}
return 1;
}/*采用邻接矩阵表示图的广度优先遍历*/
void BFS_AM(AMGraph &G,char v0)
{
/*从v0元素开始访问图*/
int u,i,v,w;
v = LocateVex(G,v0); //找到v0对应的下标
printf("%c ", v0); //打印v0
visited[v] = 1; //顶点v0已被访问
q.push(v0); //将v0入队
while (!q.empty())
{
u = q.front(); //将队头元素u出队,开始访问u的所有邻接点
v = LocateVex(G, u); //得到顶点u的对应下标
q.pop(); //将顶点u出队
for (i = 0; i < G.vexnum; i++)
{
w = G.vexs[i];
if (G.arcs[v][i] && !visited[i])//顶点u和w间有边,且顶点w未被访问
{
printf("%c ", w); //打印顶点w
q.push(w); //将顶点w入队
visited[i] = 1; //顶点w已被访问
}
}
}
}/*找到顶点对应的下标*/
int LocateVex(ALGraph &G, char v)
{
int i;
for (i = 0; i < G.vexnum; i++)
if (v == G.vertices[i].data)
return i;
}/*邻接表存储表示*/
typedef struct ArcNode //边结点
{
int adjvex; //该边所指向的顶点的位置
ArcNode *nextarc; //指向下一条边的指针
int info; //和边相关的信息,如权值
}ArcNode;
typedef struct VexNode //表头结点
{
char data;
ArcNode *firstarc; //指向第一条依附该顶点的边的指针
}VexNode,AdjList[MVNum]; //AbjList表示一个表头结点表
typedef struct ALGraph
{
AdjList vertices;
int vexnum, arcnum;
}ALGraph;/*采用邻接表表示法,创建无向图G*/
int CreateUDG_2(ALGraph &G)
{
int i, j, k;
char v1, v2;
scanf("%d%d", &G.vexnum, &G.arcnum); //输入总顶点数,总边数
getchar();
for (i = 0; i < G.vexnum; i++) //输入各顶点,构造表头结点表
{
scanf("%c", &G.vertices[i].data); //输入顶点值
G.vertices[i].firstarc = NULL; //初始化每个表头结点的指针域为NULL
}
for (k = 0; k < G.arcnum; k++) //输入各边,构造邻接表
{
getchar();
scanf("%c%c", &v1, &v2); //输入一条边依附的两个顶点
i = LocateVex(G, v1); //找到顶点i的下标
j = LocateVex(G, v2); //找到顶点j的下标
ArcNode *p1 = new ArcNode; //创建一个边结点*p1
p1->adjvex = j; //其邻接点域为j
p1->nextarc = G.vertices[i].firstarc; G.vertices[i].firstarc = p1; // 将新结点*p插入到顶点v1的边表头部
ArcNode *p2 = new ArcNode; //生成另一个对称的新的表结点*p2
p2->adjvex = i;
p2->nextarc = G.vertices[j].firstarc;
G.vertices[j].firstarc = p1;
}
return 1;
}/*采用邻接表表示图的广度优先遍历*/
void BFS_AL(ALGraph &G, char v0)
{
int u,w,v;
ArcNode *p;
printf("%c ", v0); //打印顶点v0
v = LocateVex(G, v0); //找到v0对应的下标
visited[v] = 1; //顶点v0已被访问
q.push(v0); //将顶点v0入队
while (!q.empty())
{
u = q.front(); //将顶点元素u出队,开始访问u的所有邻接点
v = LocateVex(G, u); //得到顶点u的对应下标
q.pop(); //将顶点u出队
for (p = G.vertices[v].firstarc; p; p = p->nextarc) //遍历顶点u的邻接点
{
w = p->adjvex;
if (!visited[w]) //顶点p未被访问
{
printf("%c ", G.vertices[w].data); //打印顶点p
visited[w] = 1; //顶点p已被访问
q.push(G.vertices[w].data); //将顶点p入队
}
}
}
}/*广度优先搜索非连通图*/
void BFSTraverse(AMGraph G)
{
int v;
for (v = 0; v < G.vexnum; v++)
visited[v] = 0; //将visited数组初始化
for (v = 0; v < G.vexnum; v++)
if (!visited[v]) BFS_AM(G, G.vexs[v]); //对尚未访问的顶点调用BFS
}深度优先搜索类似于树的先序遍历,具体过程如下:
准备工作:创建一个visited数组,用于记录所有被访问过的顶点。
1.从图中v0出发,访问v0。
2.找出v0的第一个未被访问的邻接点,访问该顶点。以该顶点为新顶点,重复此步骤,直至刚访问过的顶点没有未被访问的邻接点为止。
3.返回前一个访问过的仍有未被访问邻接点的顶点,继续访问该顶点的下一个未被访问领接点。
4.重复2,3步骤,直至所有顶点均被访问,搜索结束。
1.初始时所有顶点均未被访问,visited数组为空。
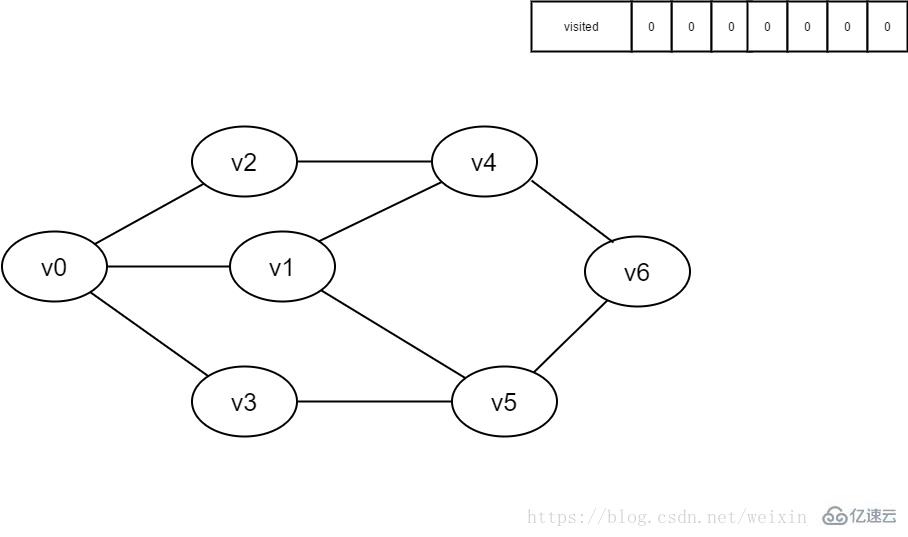
图4-2-1
2.即将访问v0。
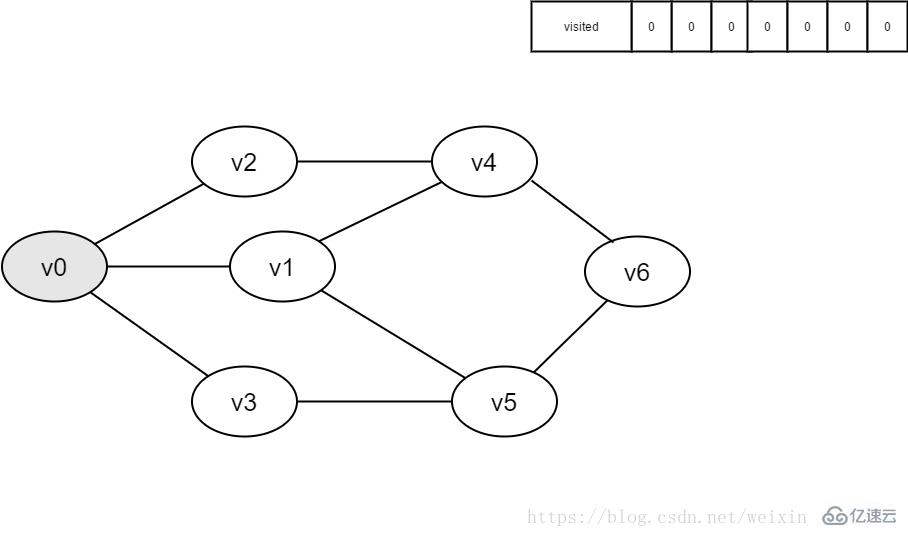
图4-2-2
3.访问v0,并将visited[0]的值置为1。
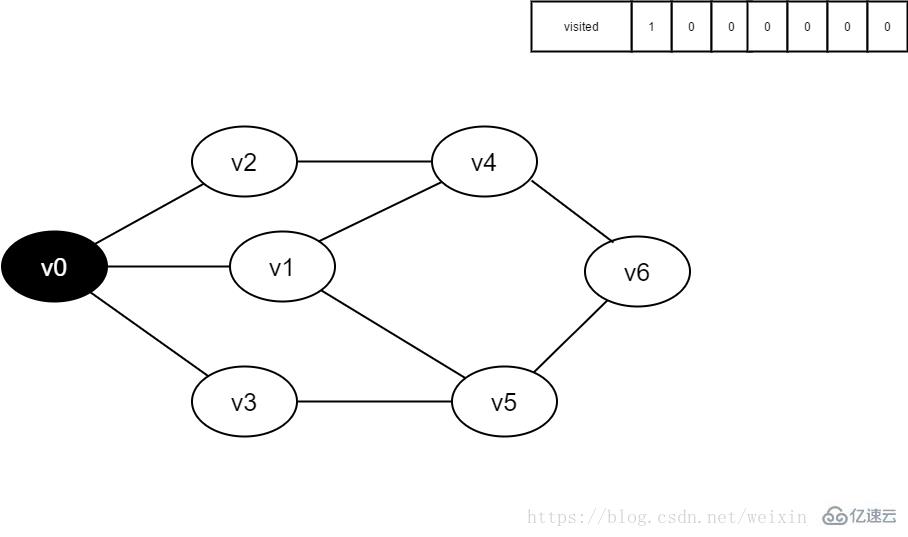
图4-2-3
4.访问v0的邻接点v2,判断visited[2],因其值为0,访问v2。
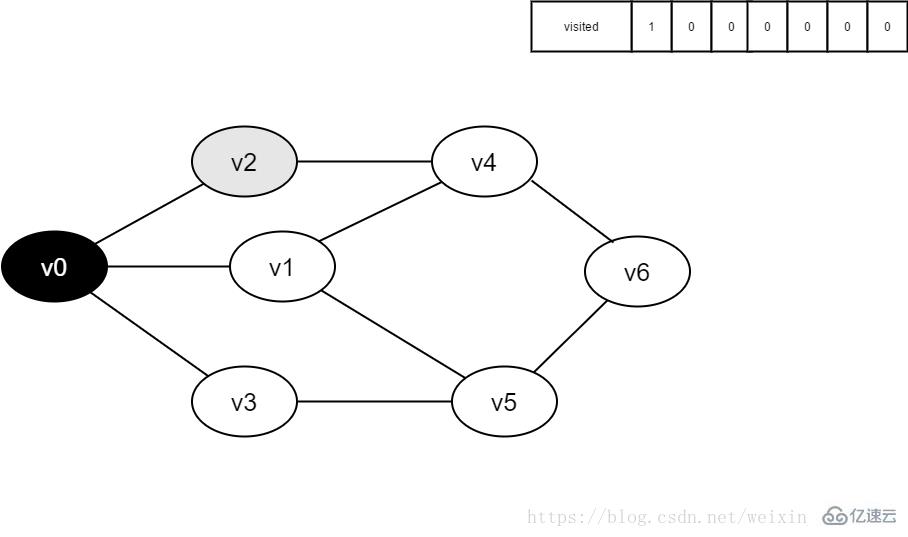
图4-2-4
5.将visited[2]置为1。
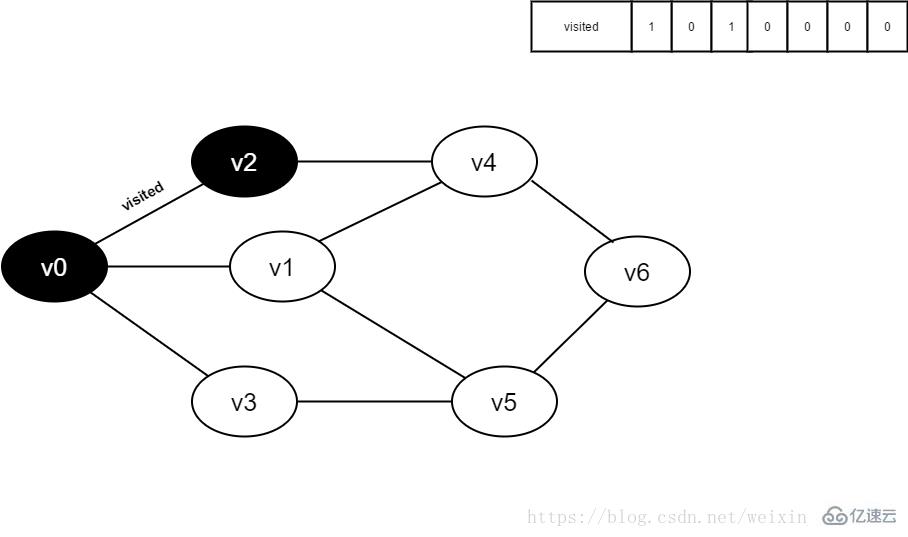
图4-2-5
6.访问v2的邻接点v0,判断visited[0],其值为1,不访问。
继续访问v2的邻接点v4,判断visited[4],其值为0,访问v4。
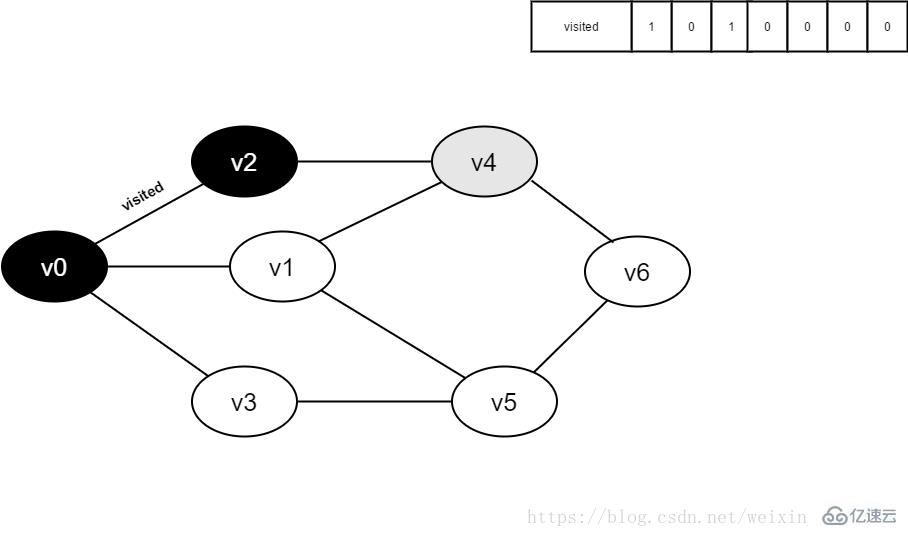
图4-2-6
7.将visited[4]置为1。
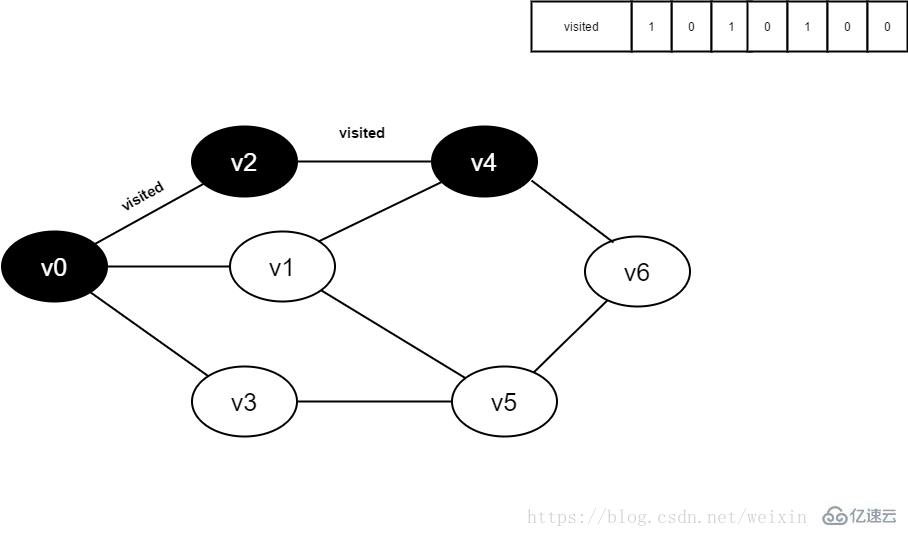
图4-2-7
8.访问v4的邻接点v1,判断visited[1],其值为0,访问v1。
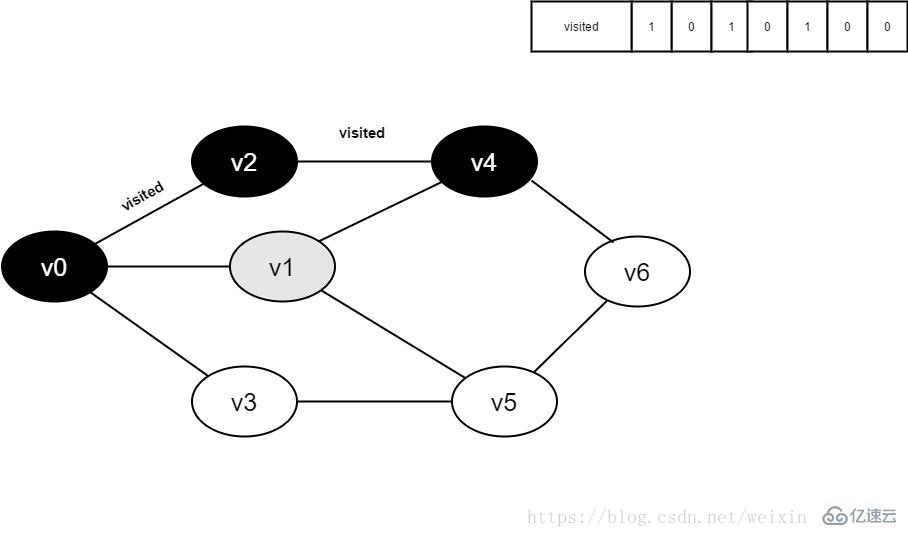
图4-2-8
9.将visited[1]置为1。
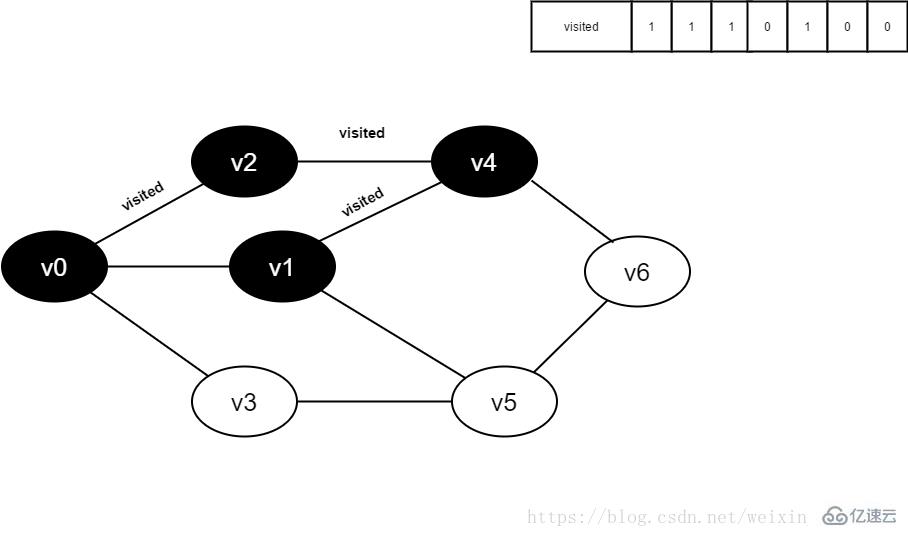
图4-2-9
10.访问v1的邻接点v0,判断visited[0],其值为1,不访问。
继续访问v1的邻接点v4,判断visited[4],其值为1,不访问。
继续访问v1的邻接点v5,判读visited[5],其值为0,访问v5。
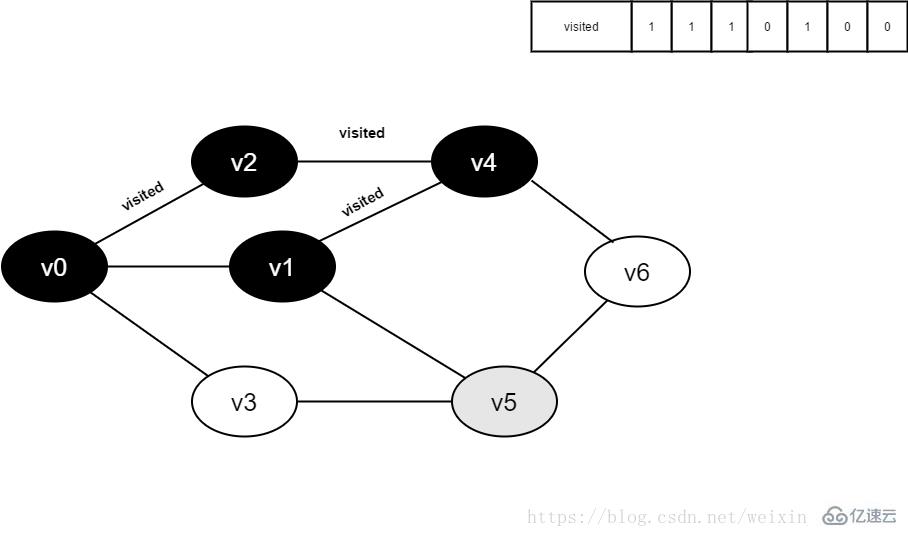
图4-2-10
11.将visited[5]置为1。
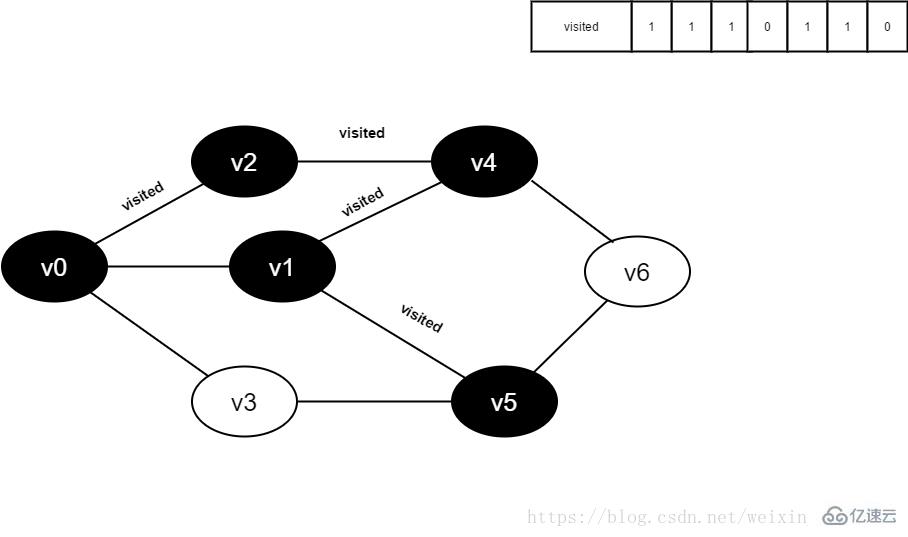
图4-2-11
12.访问v5的邻接点v1,判断visited[1],其值为1,不访问。
继续访问v5的邻接点v3,判断visited[3],其值为0,访问v3。
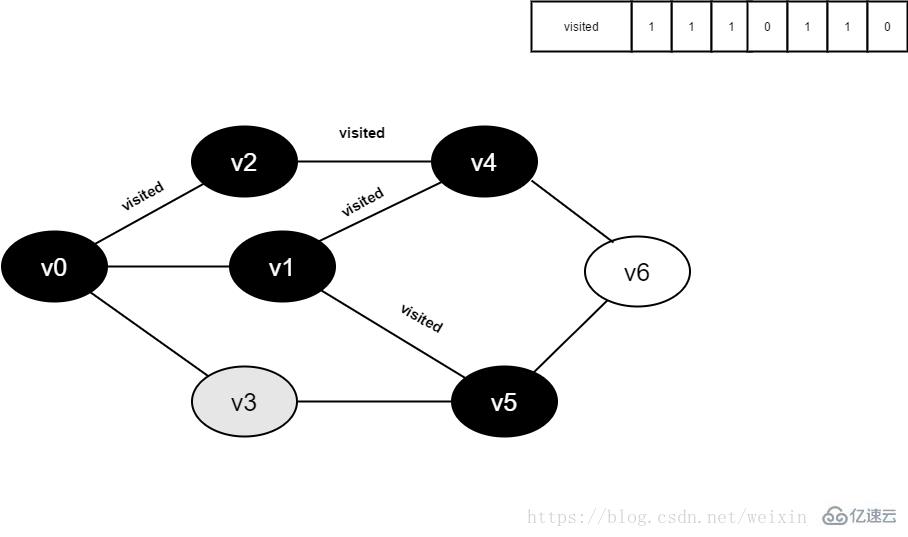
图4-2-12
13.将visited[1]置为1。
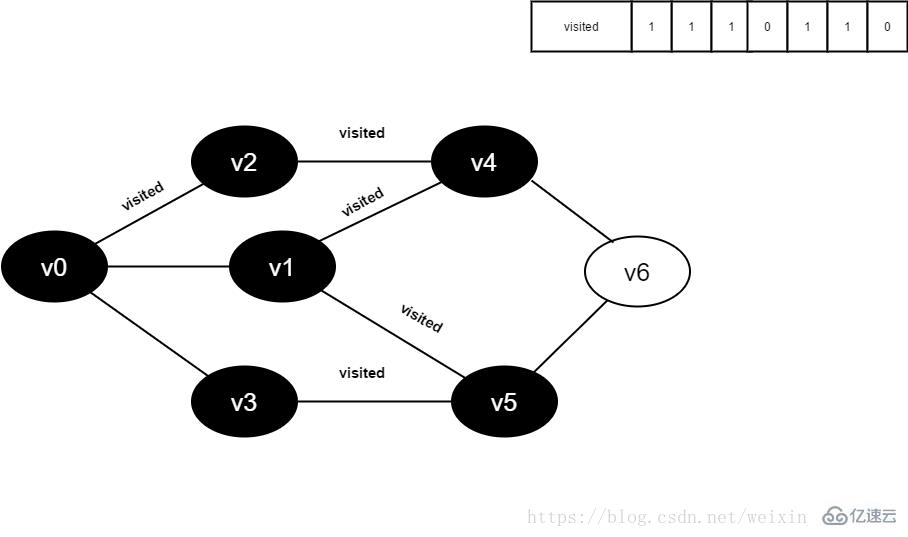
图4-2-13
14.访问v3的邻接点v0,判断visited[0],其值为1,不访问。
继续访问v3的邻接点v5,判断visited[5],其值为1,不访问。
v3所有邻接点均已被访问,回溯到其上一个顶点v5,遍历v5所有邻接点。
访问v5的邻接点v6,判断visited[6],其值为0,访问v6。
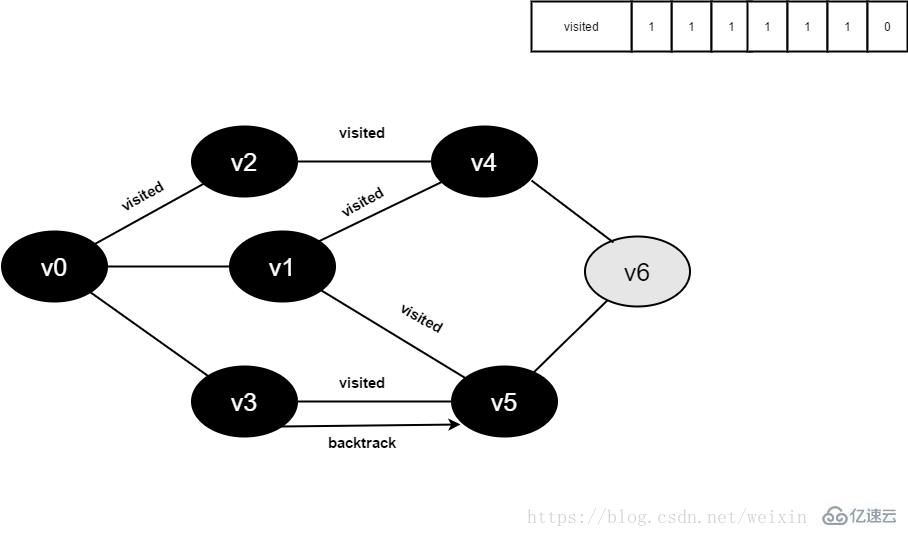
图4-2-14
15.将visited[6]置为1。
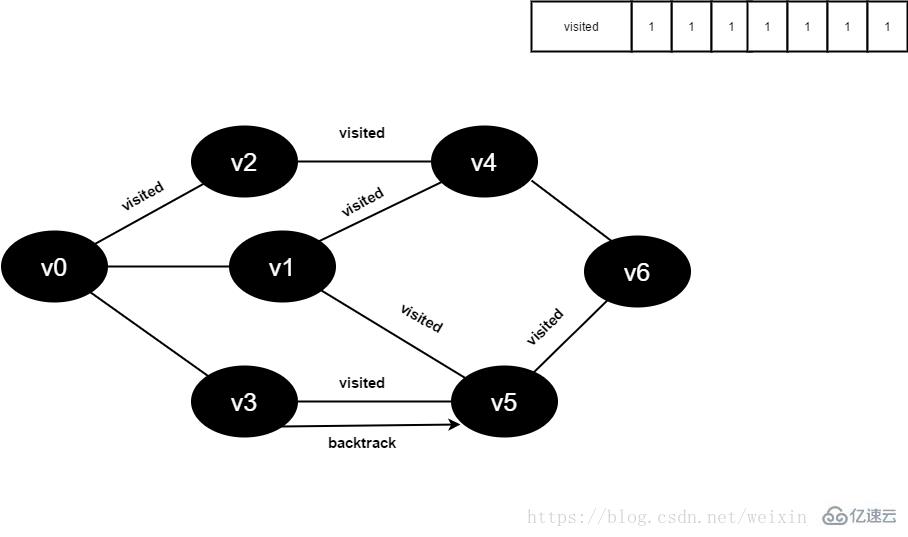
图4-2-15
16.访问v6的邻接点v4,判断visited[4],其值为1,不访问。
访问v6的邻接点v5,判断visited[5],其值为1,不访问。
v6所有邻接点均已被访问,回溯到其上一个顶点v5,遍历v5剩余邻接点。
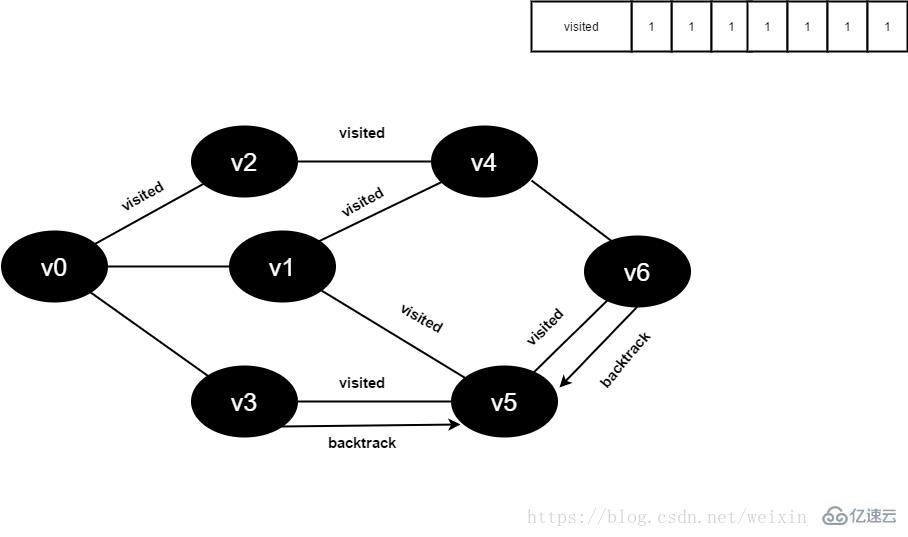
图4-2-16
17.v5所有邻接点均已被访问,回溯到其上一个顶点v1。
v1所有邻接点均已被访问,回溯到其上一个顶点v4,遍历v4剩余邻接点v6。
v4所有邻接点均已被访问,回溯到其上一个顶点v2。
v2所有邻接点均已被访问,回溯到其上一个顶点v1,遍历v1剩余邻接点v3。
v1所有邻接点均已被访问,搜索结束。
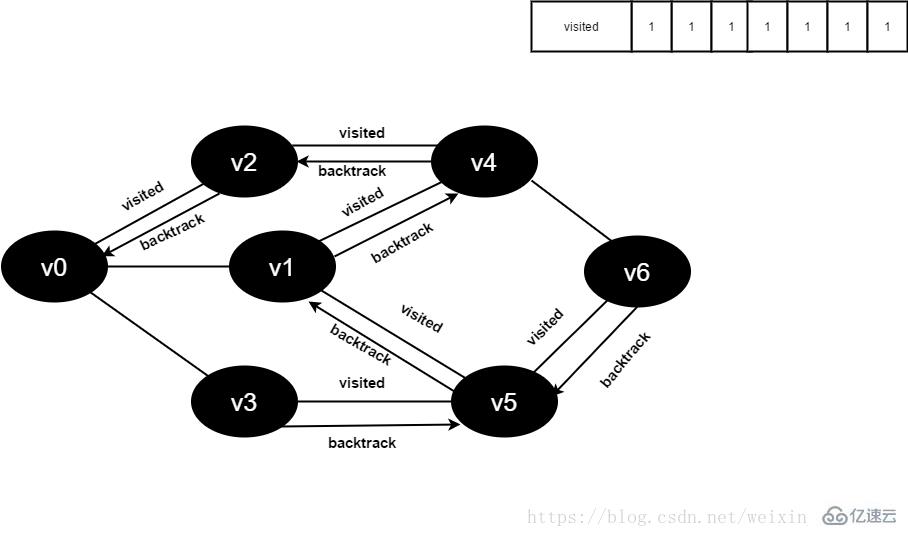
图4-2-17
邻接矩阵的创建在上述已描述过,这里不再赘述
void DFS_AM(AMGraph &G, int v)
{
int w;
printf("%c ", G.vexs[v]);
visited[v] = 1;
for (w = 0; w < G.vexnum; w++)
if (G.arcs[v][w]&&!visited[w]) //递归调用
DFS_AM(G,w);
}邻接表的创建在上述已描述过,这里不再赘述。
void DFS_AL(ALGraph &G, int v)
{
int w;
printf("%c ", G.vertices[v].data);
visited[v] = 1;
ArcNode *p = new ArcNode;
p = G.vertices[v].firstarc;
while (p)
{
w = p->adjvex;
if (!visited[w]) DFS_AL(G, w);
p = p->nextarc;
}
}关于“图的广度优先遍历算法类似于二叉树的示例分析”这篇文章就分享到这里了,希望以上内容可以对大家有一定的帮助,使各位可以学到更多知识,如果觉得文章不错,请把它分享出去让更多的人看到。
免责声明:本站发布的内容(图片、视频和文字)以原创、转载和分享为主,文章观点不代表本网站立场,如果涉及侵权请联系站长邮箱:is@yisu.com进行举报,并提供相关证据,一经查实,将立刻删除涉嫌侵权内容。