жӮЁеҘҪпјҢзҷ»еҪ•еҗҺжүҚиғҪдёӢи®ўеҚ•е“ҰпјҒ
иҝҷзҜҮж–Үз« дё»иҰҒи®Іи§ЈдәҶвҖңеҰӮдҪ•зҗҶи§ЈеёғйҡҶиҝҮж»ӨеҷЁз®—жі•зҡ„е®һзҺ°еҺҹзҗҶвҖқпјҢж–Үдёӯзҡ„и®Іи§ЈеҶ…е®№з®ҖеҚ•жё…жҷ°пјҢжҳ“дәҺеӯҰд№ дёҺзҗҶи§ЈпјҢдёӢйқўиҜ·еӨ§е®¶и·ҹзқҖе°Ҹзј–зҡ„жҖқи·Ҝж…ўж…ўж·ұе…ҘпјҢдёҖиө·жқҘз ”з©¶е’ҢеӯҰд№ вҖңеҰӮдҪ•зҗҶи§ЈеёғйҡҶиҝҮж»ӨеҷЁз®—жі•зҡ„е®һзҺ°еҺҹзҗҶвҖқеҗ§пјҒ
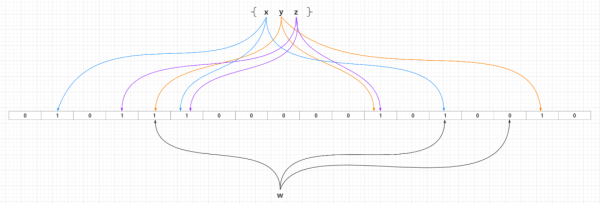
еёғйҡҶиҝҮж»ӨеҷЁзҡ„дёҖдәӣжҰӮеҝөдё»иҰҒеҢ…жӢ¬пјҡ
з®Җд»Ӣ
з®—жі•
еҸӮж•°
дјҳеҠҝе’ҢеҠЈеҠҝ
еёғйҡҶиҝҮж»ӨеҷЁз®Җд»Ӣ
еёғйҡҶиҝҮж»ӨеҷЁжҳҜгҖҢдёҖз§Қз©әй—ҙй«ҳж•ҲжҰӮзҺҮжҖ§зҡ„ж•°жҚ®з»“жһ„гҖҚ(зҷҫ科дёӯеҺҹж–ҮжҳҜa space-efficient probabilistic data structure)пјҢиҜҘж•°жҚ®з»“жһ„дәҺ1970е№ҙз”ұBurton Howard BloomжҸҗеҮәпјҢгҖҢдҪңз”ЁжҳҜжөӢиҜ•дёҖдёӘе…ғзҙ жҳҜеҗҰжҹҗдёӘйӣҶеҗҲзҡ„дёҖдёӘжҲҗе‘ҳгҖҚгҖӮеёғйҡҶиҝҮж»ӨеҷЁжҳҜеҸҜиғҪеҮәзҺ°false positive(иҝҷдёӘжҳҜдё“жңүеҗҚиҜҚ"еҒҮйҳіжҖ§"пјҢеҸҜд»ҘзҗҶи§ЈдёәиҜҜеҲӨзҡ„жғ…еҶөпјҢдёӢж–ҮеҰӮжһңз”ЁеҲ°иҝҷдёӘеҗҚиҜҚдјҡдҝқз•ҷиӢұж–ҮеҚ•иҜҚдҪҝз”Ё)еҢ№й…Қзҡ„пјҢжҚўиЁҖд№ӢпјҢеёғйҡҶиҝҮж»ӨеҷЁеңЁдҪҝз”Ёзҡ„ж—¶еҖҷжңүеҸҜиғҪиҝ”еӣһз»“жһң"еҸҜиғҪеӯҳеңЁдәҺйӣҶеҗҲдёӯ"жҲ–иҖ…"еҝ…е®ҡдёҚеӯҳеңЁдәҺйӣҶеҗҲдёӯ"гҖӮ
еёғйҡҶиҝҮж»ӨеҷЁз®—жі•жҸҸиҝ°
еңЁеңәжҷҜеӨҚжқӮзҡ„зҪ‘з»ңзҲ¬иҷ«дёӯпјҢзҲ¬еҸ–еҲ°зҡ„зҪ‘йЎөURLдҫқиө–жңүеҸҜиғҪжҲҗзҺҜпјҢдҫӢеҰӮеңЁURL-1йЎөйқўдёӯеұ•зӨәдәҶURL-2пјҢ然еҗҺеҸҲеңЁURL-2дёӯзҡ„йЎөйқўеұ•зӨәдәҶURL-1пјҢиҝҷдёӘж—¶еҖҷйңҖиҰҒдёҖз§Қж–№жЎҲи®°еҪ•е’ҢеҲӨж–ӯеҺҶеҸІи®ҝй—®иҝҮзҡ„URLгҖӮиҝҷдёӘж—¶еҖҷеҸҜиғҪдјҡжғіеҲ°дёӢйқўзҡ„ж–№жЎҲпјҡ
ж–№жЎҲдёҖпјҡдҪҝз”Ёж•°жҚ®еә“еӯҳеӮЁе·Із»Ҹи®ҝй—®иҝҮзҡ„URLпјҢдҫӢеҰӮMySQLиЎЁдёӯеҹәдәҺURLе»әз«Ӣе”ҜдёҖзҙўеј•жҲ–иҖ…дҪҝз”ЁRedisзҡ„SETж•°жҚ®зұ»еһӢ
ж–№жЎҲдәҢпјҡдҪҝз”ЁHashSet(е…¶е®һиҝҷйҮҢдёҚеұҖйҷҗдәҺHashSetпјҢй“ҫиЎЁгҖҒж ‘е’Ңж•ЈеҲ—иЎЁзӯүж•°жҚ®з»“жһ„йғҪиғҪж»Ўи¶і)еӯҳеӮЁе·Із»Ҹи®ҝй—®иҝҮзҡ„URL
ж–№жЎҲдёүпјҡеҹәдәҺж–№жЎҲдёҖе’Ңж–№жЎҲдәҢиҝӣиЎҢдјҳеҢ–пјҢеӯҳеӮЁURLзҡ„ж‘ҳиҰҒпјҢдҪҝз”Ёж‘ҳиҰҒз®—жі•еҰӮMD5гҖҒSHA-nз®—жі•й’ҲеҜ№URLеӯ—з¬ҰдёІз”ҹжҲҗж‘ҳиҰҒ
ж–№жЎҲеӣӣпјҡдҪҝз”ЁHashеҮҪж•°еӨ„зҗҶеҜ№еә”зҡ„URLз”ҹжҲҗдёҖдёӘе“ҲеёҢз ҒпјҢеҶҚжҠҠе“ҲеёҢз ҒйҖҡиҝҮдёҖдёӘжҳ е°„еҮҪж•°жҳ е°„еҲ°дёҖдёӘеӣәе®ҡе®№йҮҸзҡ„BitSetдёӯзҡ„жҹҗдёҖдёӘжҜ”зү№
еҜ№дәҺж–№жЎҲдёҖгҖҒж–№жЎҲдәҢе’Ңж–№жЎҲдёүпјҢеңЁеҺҶеҸІи®ҝй—®URLж•°жҚ®йҮҸжһҒеӨ§зҡ„жғ…еҶөдёӢпјҢдјҡж¶ҲиҖ—е·ЁеӨ§зҡ„еӯҳеӮЁз©әй—ҙ(зЈҒзӣҳжҲ–иҖ…еҶ…еӯҳ)пјҢеҜ№дәҺж–№жЎҲеӣӣпјҢеҰӮжһңURLжңү100дәҝдёӘпјҢйӮЈд№ҲиҰҒжҠҠеҶІзӘҒеҮ зҺҮйҷҚдҪҺеҲ°1%пјҢйӮЈд№ҲBitSetзҡ„е®№йҮҸйңҖиҰҒи®ҫзҪ®дёә10000дәҝгҖӮ
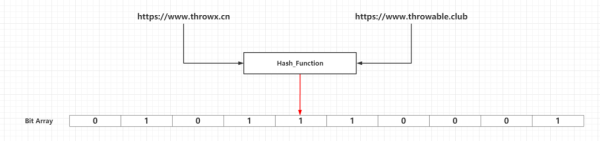
жүҖд»ҘдёҠйқўзҡ„еӣӣз§Қж–№жЎҲйғҪжңүжҳҺжҳҫзҡ„дёҚи¶ід№ӢеӨ„пјҢиҖҢеёғйҡҶиҝҮж»ӨеҷЁз®—жі•зҡ„еҹәжң¬жҖқи·Ҝи·ҹж–№жЎҲеӣӣе·®дёҚеӨҡпјҢжңҖеӨ§зҡ„дёҚеҗҢзӮ№е°ұжҳҜж–№жЎҲеӣӣдёӯеҸӘжҸҗеҲ°дҪҝз”ЁдәҶдёҖдёӘж•ЈеҲ—еҮҪж•°пјҢиҖҢеёғйҡҶиҝҮж»ӨеҷЁдёӯдҪҝз”ЁдәҶk(k >= 1)дёӘзӣёдә’зӢ¬з«Ӣзҡ„й«ҳж•ҲдҪҺеҶІзӘҒзҡ„ж•ЈеҲ—еҮҪж•°гҖӮ
дёҖдёӘеҲқе§ӢеҢ–зҡ„еёғйҡҶиҝҮж»ӨеҷЁжҳҜдёҖдёӘжүҖжңүжҜ”зү№йғҪи®ҫзҪ®дёә0зҡ„й•ҝеәҰдёәmзҡ„жҜ”зү№ж•°з»„пјҢд№ҹе°ұжҳҜи®ӨзҹҘдёӯзҡ„Bit ArrayгҖҒBit SetжҲ–иҖ…Redisдёӯзҡ„Bit MapжҰӮеҝөгҖӮ然еҗҺйңҖиҰҒеј•е…ҘkдёӘдёҚеҗҢзҡ„ж•ЈеҲ—еҮҪж•°пјҢжҹҗдёӘж–°еўһе…ғзҙ йҖҡиҝҮиҝҷkдёӘж•ЈеҲ—еҮҪж•°еӨ„зҗҶд№ӢеҗҺпјҢжҳ е°„еҲ°жҜ”зү№ж•°з»„mдёӘжҜ”зү№дёӯзҡ„kдёӘпјҢ并且жҠҠиҝҷдәӣе‘Ҫдёӯжҳ е°„зҡ„kдёӘжҜ”зү№дҪҚи®ҫзҪ®дёә1пјҢдә§з”ҹдёҖдёӘеқҮеҢҖзҡ„йҡҸжңәеҲҶеёғгҖӮйҖҡеёёжғ…еҶөдёӢпјҢkзҡ„дёҖдёӘиҫғе°Ҹзҡ„еёёж•°пјҢеҸ–еҶідәҺжүҖйңҖзҡ„иҜҜеҲӨзҺҮпјҢиҖҢеёғйҡҶиҝҮж»ӨеҷЁе®№йҮҸmдёҺж•ЈеҲ—еҮҪж•°дёӘж•°kе’ҢйңҖиҰҒж·»еҠ е…ғзҙ ж•°йҮҸе‘ҲжӯЈзӣёе…ігҖӮ
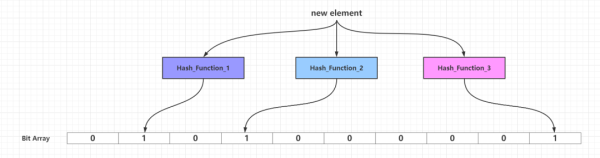
еҪ“йңҖиҰҒж–°еўһзҡ„жүҖжңүе…ғзҙ йғҪж·»еҠ еҲ°еёғйҡҶиҝҮж»ӨеҷЁд№ӢеҗҺпјҢйӮЈд№ҲжҜ”зү№ж•°з»„дёӯзҡ„еҫҲеӨҡжҜ”зү№йғҪиў«и®ҫзҪ®дёә1гҖӮиҝҷдёӘж—¶еҖҷеҰӮжһңйңҖиҰҒеҲӨж–ӯдёҖдёӘе…ғзҙ жҳҜеҗҰеӯҳеңЁдәҺеёғйҡҶиҝҮж»ӨеҷЁдёӯпјҢеҸӘйңҖиҰҒйҖҡиҝҮkдёӘж•ЈеҲ—еҮҪж•°еӨ„зҗҶеҫ—еҲ°жҜ”зү№ж•°з»„зҡ„kдёӘдёӢж ҮпјҢ然еҗҺеҲӨж–ӯжҜ”зү№ж•°з»„еҜ№еә”зҡ„дёӢж ҮжүҖеңЁжҜ”зү№жҳҜеҗҰдёә1гҖӮеҰӮжһңиҝҷkдёӘдёӢж ҮжүҖеңЁжҜ”зү№дёӯгҖҢиҮіе°‘еӯҳеңЁдёҖдёӘ0пјҢйӮЈд№ҲиҝҷдёӘйңҖиҰҒеҲӨж–ӯзҡ„е…ғзҙ еҝ…е®ҡдёҚеңЁеёғйҡҶиҝҮж»ӨеҷЁд»ЈиЎЁзҡ„йӣҶеҗҲдёӯгҖҚ;еҰӮжһңиҝҷkдёӘдёӢж ҮжүҖеңЁжҜ”зү№е…ЁйғЁйғҪдёә1пјҢйӮЈд№ҲйӮЈд№ҲиҝҷдёӘйңҖиҰҒеҲӨж–ӯзҡ„е…ғзҙ гҖҢеҸҜиғҪеӯҳеңЁдәҺгҖҚеёғйҡҶиҝҮж»ӨеҷЁд»ЈиЎЁзҡ„йӣҶеҗҲдёӯжҲ–иҖ…еҲҡеҘҪжҳҜдёҖдёӘFalse PositiveпјҢиҮідәҺиҜҜе·®зҺҮеҲҶжһҗи§ҒдёӢж–Үзҡ„гҖҢеёғйҡҶиҝҮж»ӨеҷЁзҡ„зӣёе…іеҸӮж•°гҖҚдёҖиҠӮгҖӮFalse PositiveеҮәзҺ°зҡ„жғ…еҶөеҸҜд»Ҙи§ҒдёӢеӣҫпјҡ
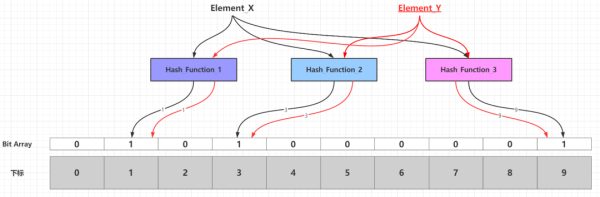
еҪ“ж·»еҠ еҲ°еёғйҡҶиҝҮж»ӨеҷЁзҡ„е…ғзҙ ж•°йҮҸжҜ”иҫғеӨ§пјҢ并且еёғйҡҶиҝҮж»ӨеҷЁзҡ„е®№йҮҸи®ҫзҪ®дёҚеҗҲзҗҶ(иҝҮе°Ҹ)пјҢе®№жҳ“еҮәзҺ°еӨҡдёӘе…ғзҙ йҖҡиҝҮkдёӘж•ЈеҲ—еҮҪж•°пјҢжҳ е°„еҲ°зӣёеҗҢзҡ„kдёӘдҪҚ(еҰӮдёҠеӣҫзҡ„дёӢж Ү1гҖҒ3гҖҒ9жүҖеңЁзҡ„дҪҚ)пјҢиҝҷдёӘж—¶еҖҷе°ұж— жі•еҮҶзЎ®еҲӨж–ӯиҝҷkдёӘдҪҚз”ұе…·дҪ“йӮЈдёӘе…ғзҙ жҳ е°„иҖҢжқҘгҖӮе…¶е®һеҸҜд»ҘжһҒз«ҜдёҖзӮ№жҖқиҖғпјҡеҒҮи®ҫеёғйҡҶиҝҮж»ӨеҷЁе®№йҮҸдёә24пјҢж•ЈеҲ—еҮҪж•°еҸӘжңүдёҖдёӘпјҢйӮЈд№Ҳж·»еҠ жңҖеӨҡ25дёӘдёҚеҗҢе…ғзҙ пјҢеҝ…е®ҡжңүдёӨдёӘдёҚеҗҢзҡ„е…ғзҙ зҡ„жҳ е°„з»“жһңиҗҪеңЁеҗҢдёҖдёӘдҪҚгҖӮ
еёғйҡҶиҝҮж»ӨеҷЁзҡ„зӣёе…іеҸӮж•°
еңЁз®—жі•жҸҸиҝ°дёҖиҠӮе·Із»ҸжҸҗеҲ°иҝҮпјҢеёғйҡҶиҝҮж»ӨеҷЁдё»иҰҒжңүдёӢйқўзҡ„еҸӮж•°пјҡ
еҲқе§ӢеҢ–жҜ”зү№ж•°з»„е®№йҮҸm
ж•ЈеҲ—еҮҪж•°дёӘж•°k
иҜҜеҲӨзҺҮε(ж•°еӯҰз¬ҰеҸ·EpsilonпјҢд»ЈиЎЁFalse Positive Rate)
йңҖиҰҒж·»еҠ еҲ°еёғйҡҶиҝҮж»ӨеҷЁзҡ„е…ғзҙ ж•°йҮҸn
иҖғиҷ‘еҲ°зҜҮе№…еҺҹеӣ пјҢиҝҷйҮҢдёҚеҒҡиҝҷеҮ дёӘеҖјзҡ„е…ізі»жҺЁеҜјпјҢзӣҙжҺҘж•ҙзҗҶеҮәз»“жһңе’Ңе…ізі»ејҸгҖӮ
иҜҜеҲӨзҺҮεзҡ„дј°з®—еҖјдёәпјҡ[1 - e^(-kn/m)]^k
жңҖдјҳж•ЈеҲ—еҮҪж•°ж•°йҮҸkзҡ„жҺЁз®—еҖјпјҡеҜ№дәҺз»ҷе®ҡзҡ„mе’ҢnпјҢеҪ“k = m/n * ln2зҡ„ж—¶еҖҷпјҢиҜҜеҲӨзҺҮεжңҖдҪҺ
жҺЁз®—еҲқе§ӢеҢ–жҜ”зү№е®№йҮҸmзҡ„еҖјпјҢеҪ“k = m/n * ln2зҡ„ж—¶еҖҷпјҢm >= n * log2(e) * log2(1/ε)
иҝҷйҮҢиҙҙдёҖдёӘеҸӮиҖғиө„ж–ҷдёӯm/nгҖҒkе’ҢFalse Positive Rateд№Ӣй—ҙзҡ„е…ізі»еӣҫпјҡ
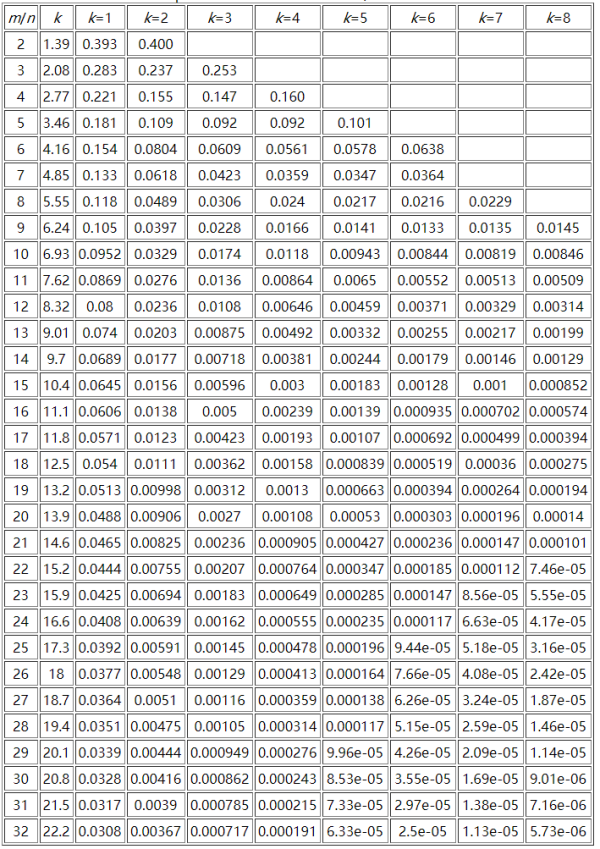
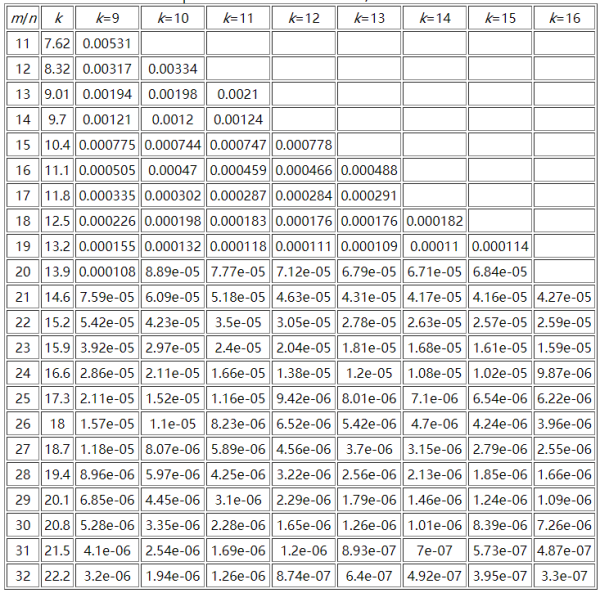
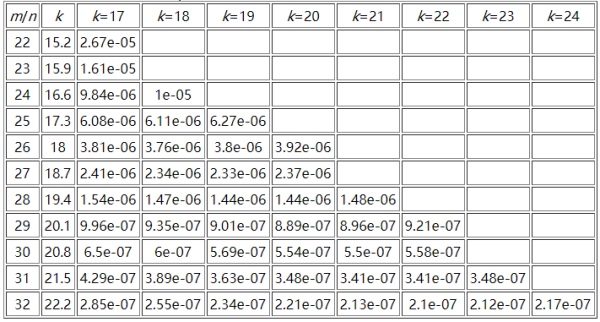
иҝҷйҮҢеҸҜд»ҘжҺЁз®—дёҖдёӢиЎЁж јдёӯжңҖеӨ§еҸӮж•°жүҖйңҖиҰҒзҡ„з©әй—ҙжһҒйҷҗпјҢеҒҮи®ҫnдёә10дәҝпјҢm/n = 32пјҢйӮЈд№Ҳmдёә320дәҝпјҢиҖҢkдёә24пјҢжӯӨж—¶зҡ„иҜҜеҲӨзҺҮдёә2.17e-07(0.000000217)пјҢйңҖиҰҒз©әй—ҙ3814.69727mгҖӮдёҖиҲ¬и§„еҫӢжҳҜпјҡ
еҪ“kеӣәе®ҡзҡ„ж—¶еҖҷпјҢm/nи¶ҠеӨ§пјҢиҜҜеҲӨзҺҮи¶Ҡе°Ҹ
еҪ“m/nеӣәе®ҡзҡ„ж—¶еҖҷпјҢkи¶ҠеӨ§пјҢиҜҜеҲӨзҺҮи¶ҠеӨ§
йҖҡеёёжғ…еҶөдёӢпјҢkйңҖиҰҒеӣәе®ҡпјҢиҖҢnжҳҜж— жі•зЎ®е®ҡеҮҶзЎ®еҖјпјҢжңҖеҘҪиҰҒиҜ„дј°еўһй•ҝи¶ӢеҠҝйў„е…Ҳи®Ўз®—дёҖдёӘжҜ”иҫғеӨ§зҡ„mеҖјеҺ»йҷҚдҪҺиҜҜеҲӨзҺҮпјҢеҪ“然д№ҹиҰҒжқғиЎЎmеҖјиҝҮеӨ§еҜјиҮҙз©әй—ҙж¶ҲиҖ—иҝҮеӨ§зҡ„й—®йўҳгҖӮ
既然еҸӮж•°зҡ„е…ізі»ејҸйғҪе·Із»ҸжңүжҺЁеҜјз»“жһңпјҢеҸҜд»ҘеҹәдәҺе…ізі»ејҸеҶҷдёҖдёӘеҸӮж•°з”ҹжҲҗеҷЁпјҡ
import java.math.BigDecimal; import java.math.RoundingMode; public class BloomFilterParamGenerator { public BigDecimal falsePositiveRate(int m, int n, int k) { double temp = Math.pow(1 - Math.exp(Math.floorDiv(-k * n, m)), k); return BigDecimal.valueOf(temp).setScale(10, RoundingMode.FLOOR); } public BigDecimal kForMinFalsePositiveRate(int m, int n) { BigDecimal k = BigDecimal.valueOf(Math.floorDiv(m, n) * Math.log(2)); return k.setScale(10, RoundingMode.FLOOR); } public BigDecimal bestM(int n, double falsePositiveRate) { double temp = log2(Math.exp(1) + Math.floor(1 / falsePositiveRate)); return BigDecimal.valueOf(n).multiply(BigDecimal.valueOf(temp)).setScale(10, RoundingMode.FLOOR); } public double log2(double x) { return Math.log(x) / Math.log(2); } public static void main(String[] args) { BloomFilterParamGenerator generator = new BloomFilterParamGenerator(); System.out.println(generator.falsePositiveRate(2, 1, 2)); // 0.3995764008 System.out.println(generator.kForMinFalsePositiveRate(32, 1)); // 22.1807097779 System.out.println(generator.bestM(1, 0.3995764009)); // 2.2382615950 } }иҝҷйҮҢзҡ„и®Ўз®—жІЎжңүиҖғиҷ‘дёҘж јзҡ„иҝӣдҪҚе’ҢжҲӘж–ӯпјҢжүҖд»Ҙе’Ңе®һйҷ…зҡ„з»“жһңеҸҜиғҪжңүеҒҸе·®пјҢеҸӘжҸҗдҫӣдёҖдёӘеҸӮиҖғзҡ„дҫӢеӯҗгҖӮ
еёғйҡҶиҝҮж»ӨеҷЁзҡ„дјҳеҠҝе’ҢеҠЈеҠҝ
еёғйҡҶиҝҮж»ӨеҷЁзҡ„дјҳеҠҝпјҡ
еёғйҡҶиҝҮж»ӨеҷЁзӣёеҜ№дәҺе…¶д»–ж•°жҚ®з»“жһ„еңЁж—¶з©әдёҠжңүе·ЁеӨ§дјҳеҠҝпјҢеҚ з”ЁеҶ…еӯҳе°‘пјҢжҹҘиҜўе’ҢжҸ’е…Ҙе…ғзҙ зҡ„ж—¶й—ҙеӨҚжқӮеәҰйғҪжҳҜO(k)
еҸҜд»ҘеҮҶзЎ®еҲӨж–ӯе…ғзҙ дёҚеӯҳеңЁдәҺеёғйҡҶиҝҮж»ӨеҷЁдёӯзҡ„еңәжҷҜ
ж•ЈеҲ—еҮҪж•°еҸҜд»ҘзӢ¬з«Ӣи®ҫи®Ў
еёғйҡҶиҝҮж»ӨеҷЁдёҚйңҖиҰҒеӯҳеӮЁе…ғзҙ жң¬иә«пјҢйҖӮз”ЁдәҺжҹҗдәӣж•°жҚ®ж•Ҹж„ҹе’Ңж•°жҚ®дёҘж јдҝқеҜҶзҡ„еңәжҷҜ
еёғйҡҶиҝҮж»ӨеҷЁзҡ„еҠЈеҠҝпјҡ
дёҚиғҪеҮҶзЎ®еҲӨж–ӯе…ғзҙ еҝ…е®ҡеӯҳеңЁдәҺеёғйҡҶиҝҮж»ӨеҷЁдёӯзҡ„еңәжҷҜпјҢеӯҳеңЁиҜҜеҲӨзҺҮпјҢеңЁkе’Ңmеӣәе®ҡзҡ„жғ…еҶөдёӢпјҢж·»еҠ зҡ„е…ғзҙ и¶ҠеӨҡпјҢиҜҜеҲӨзҺҮи¶Ҡй«ҳ
жІЎжңүеӯҳеӮЁе…ЁйҮҸзҡ„е…ғзҙ пјҢеҜ№дәҺдёҖдәӣеҮҶзЎ®жҹҘиҜўжҲ–иҖ…еҮҶзЎ®з»ҹи®Ўзҡ„еңәжҷҜдёҚйҖӮз”Ё
еҺҹз”ҹзҡ„еёғйҡҶиҝҮж»ӨеҷЁж— жі•е®үе…Ёең°еҲ йҷӨе…ғзҙ
иҝҷйҮҢз•ҷдёҖдёӘеҫҲз®ҖеҚ•зҡ„й—®йўҳз»ҷиҜ»иҖ…пјҡдёәд»Җд№ҲеҺҹз”ҹзҡ„еёғйҡҶиҝҮж»ӨеҷЁж— жі•е®үе…Ёең°еҲ йҷӨе…ғзҙ ?(еҸҜд»Ҙзҝ»зңӢд№ӢеүҚзҡ„False Positiveд»Ӣз»Қ)
еёғйҡҶиҝҮж»ӨеҷЁз®—жі•е®һзҺ°
и‘—еҗҚзҡ„Javaе·Ҙе…·зұ»еә“GuavaдёӯиҮӘеёҰдәҶдёҖдёӘbetaзүҲжң¬зҡ„еёғйҡҶиҝҮж»ӨеҷЁе®һзҺ°пјҢиҝҷйҮҢеҸӮиҖғе…¶дёӯзҡ„жәҗз Ғе®һзҺ°жҖқи·Ҝе’ҢдёҠж–Үдёӯзҡ„з®—жі•жҸҸиҝ°иҝӣиЎҢдёҖж¬ЎеёғйҡҶиҝҮж»ӨеҷЁзҡ„е®һзҺ°гҖӮе…ҲиҖғиҷ‘и®ҫи®Ўж•ЈеҲ—еҮҪж•°пјҢз®ҖеҚ•дёҖзӮ№зҡ„ж–№ејҸе°ұжҳҜеҸӮиҖғJavaBeanзҡ„hashCode()ж–№жі•зҡ„и®ҫи®Ўпјҡ
// дёӢйқўзҡ„ж–№жі•жқҘжәҗдәҺjava.util.Arrays#hashCode public static int hashCode(Object a[]) { if (a == null) return 0; int result = 1; for (Object element : a) result = 31 * result + (element == null ? 0 : element.hashCode()); return result; }дёҠйқўж–№жі•зҡ„31еҸҜд»ҘдҪңдёәдёҖдёӘиҫ“е…Ҙзҡ„seedпјҢжҜҸдёӘж•ЈеҲ—еҮҪж•°и®ҫи®ЎдёҖдёӘзӢ¬з«Ӣзҡ„seedпјҢ并且иҝҷдёӘseedеҖјйҖүз”Ёзҙ ж•°еҹәдәҺеӯ—з¬ҰдёІдёӯзҡ„жҜҸдёӘcharиҝӣиЎҢиҝӯеҠ е°ұиғҪе®һзҺ°и®Ўз®—еҮәжқҘзҡ„з»“жһңжҳҜзӣёеҜ№зӢ¬з«Ӣзҡ„пјҡ
import java.util.Objects; public class HashFunction { /** * еёғйҡҶиҝҮж»ӨеҷЁе®№йҮҸ */ private final int m; /** * з§Қеӯҗ */ private final int seed; public HashFunction(int m, int seed) { this.m = m; this.seed = seed; } public int hash(String element) { if (Objects.isNull(element)) { return 0; } int result = 1; int len = element.length(); for (int i = 0; i < len; i++) { result = seed * result + element.charAt(i); } // иҝҷйҮҢзЎ®дҝқи®Ўз®—еҮәжқҘзҡ„з»“жһңдёҚдјҡи¶…иҝҮm return (m - 1) & result; } }жҺҘзқҖе®һзҺ°еёғйҡҶиҝҮж»ӨеҷЁпјҡ
public class BloomFilter { private static final int[] K_SEED_ARRAY = {5, 7, 11, 13, 31, 37, 61, 67}; private static final int MAX_K = K_SEED_ARRAY.length; private final int m; private final int k; private final BitSet bitSet; private final HashFunction[] hashFunctions; public BloomFilter(int m, int k) { this.k = k; if (k <= 0 && k > MAX_K) { throw new IllegalArgumentException("k = " + k); } this.m = m; this.bitSet = new BitSet(m); hashFunctions = new HashFunction[k]; for (int i = 0; i < k; i++) { hashFunctions[i] = new HashFunction(m, K_SEED_ARRAY[i]); } } public void addElement(String element) { for (HashFunction hashFunction : hashFunctions) { bitSet.set(hashFunction.hash(element), true); } } public boolean contains(String element) { if (Objects.isNull(element)) { return false; } boolean result = true; for (HashFunction hashFunction : hashFunctions) { result = result && bitSet.get(hashFunction.hash(element)); } return result; } public int m() { return m; } public int k() { return k; } public static void main(String[] args) { BloomFilter bf = new BloomFilter(24, 3); bf.addElement("throwable"); bf.addElement("throwx"); System.out.println(bf.contains("throwable")); // true } }иҝҷйҮҢзҡ„ж•ЈеҲ—з®—жі•е’Ңжңүйҷҗзҡ„kеҖјдёҚи¶ід»Ҙеә”еҜ№еӨҚжқӮзҡ„еңәжҷҜпјҢд»…д»…дёәдәҶиҜҙжҳҺеҰӮдҪ•е®һзҺ°еёғйҡҶиҝҮж»ӨеҷЁпјҢжҖ»зҡ„жқҘиҜҙпјҢеҺҹз”ҹеёғйҡҶиҝҮж»ӨеҷЁз®—жі•жҳҜжҜ”иҫғз®ҖеҚ•зҡ„гҖӮеҜ№дәҺдёҖдәӣеӨҚжқӮзҡ„з”ҹдә§еңәжҷҜпјҢеҸҜд»ҘдҪҝз”ЁдёҖдәӣзҺ°жҲҗзҡ„зұ»еә“еҰӮGuavaдёӯзҡ„еёғйҡҶиҝҮж»ӨеҷЁAPIгҖҒRedisдёӯзҡ„еёғйҡҶиҝҮж»ӨеҷЁжҸ’件жҲ–иҖ…Redisson(Redisй«ҳзә§е®ўжҲ·з«Ҝ)дёӯзҡ„еёғйҡҶиҝҮж»ӨеҷЁAPIгҖӮ
еёғйҡҶиҝҮж»ӨеҷЁеә”з”Ё
дё»иҰҒеҢ…жӢ¬пјҡ
Guavaдёӯзҡ„API
Redissonдёӯзҡ„API
дҪҝз”ЁеңәжҷҜ
дҪҝз”ЁGuavaдёӯзҡ„еёғйҡҶиҝҮж»ӨеҷЁAPI
еј•е…ҘGuavaзҡ„дҫқиө–пјҡ
<dependency> <groupId>com.google.guava</groupId> <artifactId>guava</artifactId> <version>30.1-jre</version> </dependency>
дҪҝз”ЁеёғйҡҶиҝҮж»ӨеҷЁпјҡ
import com.google.common.hash.BloomFilter; import com.google.common.hash.Funnels; import java.nio.charset.StandardCharsets; public class GuavaBloomFilter { @SuppressWarnings("UnstableApiUsage") public static void main(String[] args) { BloomFilter<CharSequence> bloomFilter = BloomFilter.create(Funnels.stringFunnel(StandardCharsets.US_ASCII), 10000, 0.0444D); bloomFilter.put("throwable"); bloomFilter.put("throwx"); System.out.println(bloomFilter.mightContain("throwable")); System.out.println(bloomFilter.mightContain("throwx")); } }жһ„йҖ BloomFilterзҡ„жңҖеӨҡеҸӮж•°зҡ„йқҷжҖҒе·ҘеҺӮж–№жі•жҳҜBloomFilter
funnelпјҡдё»иҰҒжҳҜжҠҠд»»ж„Ҹзұ»еһӢзҡ„ж•°жҚ®иҪ¬еҢ–жҲҗHashCodeпјҢжҳҜдёҖдёӘйЎ¶еұӮжҺҘеҸЈпјҢжңүеӨ§йҮҸеҶ…зҪ®е®һзҺ°пјҢи§ҒFunnels
expectedInsertionsпјҡжңҹжңӣжҸ’е…Ҙзҡ„е…ғзҙ дёӘж•°
fppпјҡзҢңжөӢжҳҜFalse Positive PercentпјҢиҜҜеҲӨзҺҮпјҢе°Ҹж•°иҖҢйқһзҷҫеҲҶж•°пјҢй»ҳи®ӨеҖј0.03
strategyпјҡжҳ е°„зӯ–з•ҘпјҢзӣ®еүҚеҸӘжңүMURMUR128_MITZ_32е’ҢMURMUR128_MITZ_64(й»ҳи®Өзӯ–з•Ҙ)
еҸӮж•°еҸҜд»ҘеҸӮз…§дёҠйқўзҡ„иЎЁж јжҲ–иҖ…еҸӮж•°з”ҹжҲҗеҷЁзҡ„жҢҮеҜјпјҢеҹәдәҺе®һйҷ…еңәжҷҜиҝӣиЎҢе®ҡеҲ¶гҖӮ
дҪҝз”ЁRedissonдёӯзҡ„еёғйҡҶиҝҮж»ӨеҷЁAPI
й«ҳзә§Redisе®ўжҲ·з«ҜRedissonе·Із»ҸеҹәдәҺRedisзҡ„bitmapж•°жҚ®з»“жһ„еҒҡдәҶе°ҒиЈ…пјҢеұҸи”ҪдәҶеӨҚжқӮзҡ„е®һзҺ°йҖ»иҫ‘пјҢеҸҜд»ҘејҖз®ұеҚіз”ЁгҖӮеј•е…ҘRedissonзҡ„дҫқиө–пјҡ
<dependency> <groupId>org.redisson</groupId> <artifactId>redisson</artifactId> <version>3.15.1</version> </dependency>
дҪҝз”ЁRedissonдёӯзҡ„еёғйҡҶиҝҮж»ӨеҷЁAPIпјҡ
import org.redisson.Redisson; import org.redisson.api.RBloomFilter; import org.redisson.api.RedissonClient; import org.redisson.config.Config; public class RedissonBloomFilter { public static void main(String[] args) { Config config = new Config(); config.useSingleServer() .setAddress("redis://127.0.0.1:6379"); RedissonClient redissonClient = Redisson.create(config); RBloomFilter<String> bloomFilter = redissonClient.getBloomFilter("ipBlockList"); // 第дёҖдёӘеҸӮж•°expectedInsertionsд»ЈиЎЁжңҹжңӣжҸ’е…Ҙзҡ„е…ғзҙ дёӘж•°пјҢ第дәҢдёӘеҸӮж•°falseProbabilityд»ЈиЎЁжңҹжңӣзҡ„иҜҜеҲӨзҺҮпјҢе°Ҹж•°иЎЁзӨә bloomFilter.tryInit(100000L, 0.03D); bloomFilter.add("127.0.0.1"); bloomFilter.add("192.168.1.1"); System.out.println(bloomFilter.contains("192.168.1.1")); // true System.out.println(bloomFilter.contains("192.168.1.2")); // false } }RedissonжҸҗдҫӣзҡ„еёғйҡҶиҝҮж»ӨеҷЁжҺҘеҸЈRBloomFilterеҫҲз®ҖеҚ•пјҡ

еёёз”Ёзҡ„ж–№жі•жңүtryInit()(еҲқе§ӢеҢ–)гҖҒadd()(ж·»еҠ е…ғзҙ )е’Ңcontains()(еҲӨж–ӯе…ғзҙ жҳҜеҗҰеӯҳеңЁ)гҖӮзӣёеҜ№дәҺGuavaзҡ„еҶ…еӯҳжҖҒзҡ„еёғйҡҶиҝҮж»ӨеҷЁе®һзҺ°пјҢRedissonжҸҗдҫӣдәҶеҹәдәҺRedisе®һзҺ°зҡ„гҖҢеҲҶеёғејҸеёғйҡҶиҝҮж»ӨеҷЁгҖҚпјҢеҸҜд»Ҙж»Ўи¶іеҲҶеёғејҸйӣҶзҫӨдёӯеёғйҡҶиҝҮж»ӨеҷЁзҡ„дҪҝз”ЁгҖӮ
еёғйҡҶиҝҮж»ӨеҷЁдҪҝз”ЁеңәжҷҜ
е…¶е®һеёғйҡҶиҝҮж»ӨеҷЁзҡ„дҪҝз”ЁеңәжҷҜеҸҜд»Ҙз”Ёзҷҫ科дёӯзҡ„дёҖеј зӨәж„ҸеӣҫжқҘжҸҸиҝ°пјҡ
еҹәдәҺдёҠеӣҫе…·дҪ“еҢ–зҡ„дёҖдәӣеңәжҷҜеҲ—дёҫеҰӮдёӢпјҡ
зҪ‘з«ҷзҲ¬иҷ«еә”з”ЁдёӯиҝӣиЎҢURLеҺ»йҮҚ(дёҚеӯҳеңЁдәҺеёғйҡҶиҝҮж»ӨеҷЁдёӯзҡ„URLеҝ…е®ҡжҳҜжңӘзҲ¬еҸ–иҝҮзҡ„URL)
йҳІзҒ«еўҷеә”з”ЁдёӯIPй»‘еҗҚеҚ•еҲӨж–ӯ(дёҚеұҖйҷҗдәҺIPй»‘еҗҚеҚ•пјҢйҖҡз”Ёзҡ„й»‘еҗҚеҚ•еҲӨж–ӯеңәжҷҜеҹәжң¬йғҪеҸҜд»ҘдҪҝз”ЁеёғйҡҶиҝҮж»ӨеҷЁпјҢдёҚеӯҳеңЁдәҺеёғйҡҶиҝҮж»ӨеҷЁдёӯзҡ„IPеҝ…е®ҡжҳҜзҷҪеҗҚеҚ•)
з”ЁдәҺ规йҒҝзј“еӯҳз©ҝйҖҸ(дёҚеӯҳеңЁдәҺеёғйҡҶиҝҮж»ӨеҷЁдёӯзҡ„KEYеҝ…е®ҡдёҚеӯҳеңЁдәҺеҗҺзҪ®зҡ„зј“еӯҳдёӯ)
еёғйҡҶиҝҮж»ӨеҷЁеҸҳдҪ“
еёғйҡҶиҝҮж»ӨеҷЁзҡ„еҸҳдҪ“еҚҒеҲҶеӨҡпјҢдё»иҰҒжҳҜдёәдәҶи§ЈеҶіеёғйҡҶиҝҮж»ӨеҷЁз®—жі•дёӯзҡ„дёҖдәӣзјәйҷ·жҲ–иҖ…еҠЈеҠҝгҖӮеёёи§Ғзҡ„еҸҳдҪ“еҰӮдёӢпјҡ
| еҸҳдҪ“еҗҚз§° | еҸҳдҪ“жҸҸиҝ° |
|---|---|
Counting Bloom Filter | жҠҠеҺҹз”ҹеёғйҡҶиҝҮж»ӨеҷЁжҜҸдёӘдҪҚжӣҝжҚўжҲҗдёҖдёӘе°Ҹзҡ„и®Ўж•°еҷЁпјҲCounterпјүпјҢжүҖи°“и®Ўж•°еҷЁе…¶е®һе°ұжҳҜдёҖдёӘе°Ҹзҡ„ж•ҙж•° |
Compressed Bloom Filter | еҜ№дҪҚж•°з»„иҝӣиЎҢеҺӢзј© |
Hierarchical Bloom Filters | еҲҶеұӮпјҢз”ұеӨҡеұӮеёғйҡҶиҝҮж»ӨеҷЁз»„жҲҗ |
Spectral Bloom Filters | CBFзҡ„жү©еұ•пјҢжҸҗдҫӣжҹҘиҜўйӣҶеҗҲе…ғзҙ зҡ„еҮәзҺ°йў‘зҺҮеҠҹиғҪ |
Bloomier Filters | еӯҳеӮЁеҮҪж•°еҖјпјҢдёҚд»…д»…жҳҜеҒҡдҪҚжҳ е°„ |
Time-Decaying Bloom Filters | и®Ўж•°еҷЁж•°з»„жӣҝжҚўдҪҚеҗ‘йҮҸпјҢдјҳеҢ–жҜҸдёӘи®Ўж•°еҷЁеӯҳеӮЁе…¶еҖјжүҖйңҖзҡ„жңҖе°Ҹз©әй—ҙ |
Space Code Bloom Filter | - |
Filter Banks | - |
Scalable Bloom filters | - |
Split Bloom Filters | - |
Retouched Bloom filters | - |
Generalized Bloom Filters | - |
Distance-sensitive Bloom filters | - |
Data Popularity Conscious Bloom Filters | - |
Memory-optimized Bloom Filter | - |
Weighted Bloom filter | - |
Secure Bloom filters | - |
иҝҷйҮҢжҢ‘йҖүCounting Bloom Filter(з®Җз§°CBF)еҸҳдҪ“зЁҚеҫ®еұ•ејҖдёҖдёӢгҖӮеҺҹз”ҹеёғйҡҶиҝҮж»ӨеҷЁзҡ„еҹәзЎҖж•°жҚ®з»“жһ„жҳҜдҪҚеҗ‘йҮҸпјҢCBFжү©еұ•еҺҹз”ҹеёғйҡҶиҝҮж»ӨеҷЁзҡ„еҹәзЎҖж•°жҚ®з»“жһ„пјҢеә•еұӮж•°з»„зҡ„жҜҸдёӘе…ғзҙ дҪҝз”Ё4дҪҚеӨ§е°Ҹзҡ„и®Ўж•°еҷЁеӯҳеӮЁж·»еҠ е…ғзҙ еҲ°ж•°з»„жҹҗдёӘдёӢж Үж—¶еҖҷжҳ е°„жҲҗеҠҹзҡ„йў‘ж¬ЎпјҢеңЁжҸ’е…Ҙж–°е…ғзҙ зҡ„ж—¶еҖҷпјҢйҖҡиҝҮkдёӘж•ЈеҲ—еҮҪж•°жҳ е°„еҲ°kдёӘе…·дҪ“и®Ўж•°еҷЁпјҢиҝҷдәӣе‘Ҫдёӯзҡ„и®Ўж•°еҷЁеҖјеўһеҠ 1;еҲ йҷӨе…ғзҙ зҡ„ж—¶еҖҷпјҢйҖҡиҝҮkдёӘж•ЈеҲ—еҮҪж•°жҳ е°„еҲ°kдёӘе…·дҪ“и®Ўж•°еҷЁпјҢиҝҷдәӣи®Ўж•°еҷЁеҖјеҮҸе°‘1гҖӮдҪҝз”ЁCBFеҲӨж–ӯе…ғзҙ жҳҜеҗҰеңЁйӣҶеҗҲдёӯзҡ„ж—¶еҖҷпјҡ
жҹҗдёӘе…ғзҙ йҖҡиҝҮkдёӘж•ЈеҲ—еҮҪж•°жҳ е°„еҲ°kдёӘе…·дҪ“и®Ўж•°еҷЁпјҢжүҖжңүи®Ўж•°еҷЁзҡ„еҖјйғҪдёә0пјҢйӮЈд№Ҳе…ғзҙ еҝ…е®ҡдёҚеңЁйӣҶеҗҲдёӯ
жҹҗдёӘе…ғзҙ йҖҡиҝҮkдёӘж•ЈеҲ—еҮҪж•°жҳ е°„еҲ°kдёӘе…·дҪ“и®Ўж•°еҷЁпјҢиҮіе°‘жңү1дёӘи®Ўж•°еҷЁзҡ„еҖјеӨ§дәҺ0пјҢйӮЈд№Ҳе…ғзҙ еҸҜиғҪеңЁйӣҶеҗҲ

е°Ҹз»“дёҖеҸҘиҜқз®ҖеҚ•жҰӮжӢ¬еёғйҡҶиҝҮж»ӨеҷЁзҡ„еҹәжң¬еҠҹиғҪпјҡгҖҢдёҚеӯҳеңЁеҲҷеҝ…дёҚеӯҳеңЁпјҢеӯҳеңЁеҲҷдёҚдёҖе®ҡеӯҳеңЁгҖӮгҖҚ
еңЁдҪҝз”ЁеёғйҡҶиҝҮж»ӨеҷЁеҲӨж–ӯдёҖдёӘе…ғзҙ жҳҜеҗҰеұһдәҺжҹҗдёӘйӣҶеҗҲж—¶пјҢдјҡжңүдёҖе®ҡзҡ„иҜҜеҲӨзҺҮгҖӮд№ҹе°ұжҳҜжңүеҸҜиғҪжҠҠдёҚеұһдәҺжҹҗдёӘйӣҶеҗҲзҡ„е…ғзҙ иҜҜеҲӨдёәеұһдәҺиҝҷдёӘйӣҶеҗҲпјҢиҝҷз§Қй”ҷиҜҜз§°дёәFalse PositiveпјҢдҪҶдёҚдјҡжҠҠеұһдәҺжҹҗдёӘйӣҶеҗҲзҡ„е…ғзҙ иҜҜеҲӨдёәдёҚеұһдәҺиҝҷдёӘйӣҶеҗҲ(зӣёеҜ№дәҺFalse PositiveпјҢ"еҒҮйҳіжҖ§"пјҢеҰӮжһңеұһдәҺжҹҗдёӘйӣҶеҗҲзҡ„е…ғзҙ иҜҜеҲӨдёәдёҚеұһдәҺиҝҷдёӘйӣҶеҗҲзҡ„жғ…еҶөз§°дёәFalse NegativeпјҢ"еҒҮйҳҙжҖ§")гҖӮFalse PositiveпјҢд№ҹе°ұжҳҜй”ҷиҜҜзҺҮжҲ–иҖ…иҜҜеҲӨзҺҮиҝҷдёӘеӣ зҙ зҡ„еј•е…ҘпјҢжҳҜеёғйҡҶиҝҮж»ӨеҷЁеңЁи®ҫи®ЎдёҠжқғиЎЎз©әй—ҙж•ҲзҺҮзҡ„е…ій”®гҖӮ
ж„ҹи°ўеҗ„дҪҚзҡ„йҳ…иҜ»пјҢд»ҘдёҠе°ұжҳҜвҖңеҰӮдҪ•зҗҶи§ЈеёғйҡҶиҝҮж»ӨеҷЁз®—жі•зҡ„е®һзҺ°еҺҹзҗҶвҖқзҡ„еҶ…е®№дәҶпјҢз»ҸиҝҮжң¬ж–Үзҡ„еӯҰд№ еҗҺпјҢзӣёдҝЎеӨ§е®¶еҜ№еҰӮдҪ•зҗҶи§ЈеёғйҡҶиҝҮж»ӨеҷЁз®—жі•зҡ„е®һзҺ°еҺҹзҗҶиҝҷдёҖй—®йўҳжңүдәҶжӣҙж·ұеҲ»зҡ„дҪ“дјҡпјҢе…·дҪ“дҪҝз”Ёжғ…еҶөиҝҳйңҖиҰҒеӨ§е®¶е®һи·өйӘҢиҜҒгҖӮиҝҷйҮҢжҳҜдәҝйҖҹдә‘пјҢе°Ҹзј–е°ҶдёәеӨ§е®¶жҺЁйҖҒжӣҙеӨҡзӣёе…ізҹҘиҜҶзӮ№зҡ„ж–Үз« пјҢж¬ўиҝҺе…іжіЁпјҒ
е…ҚиҙЈеЈ°жҳҺпјҡжң¬з«ҷеҸ‘еёғзҡ„еҶ…е®№пјҲеӣҫзүҮгҖҒи§Ҷйў‘е’Ңж–Үеӯ—пјүд»ҘеҺҹеҲӣгҖҒиҪ¬иҪҪе’ҢеҲҶдә«дёәдё»пјҢж–Үз« и§ӮзӮ№дёҚд»ЈиЎЁжң¬зҪ‘з«ҷз«ӢеңәпјҢеҰӮжһңж¶үеҸҠдҫөжқғиҜ·иҒ”зі»з«ҷй•ҝйӮ®з®ұпјҡis@yisu.comиҝӣиЎҢдёҫжҠҘпјҢ并жҸҗдҫӣзӣёе…іиҜҒжҚ®пјҢдёҖз»ҸжҹҘе®һпјҢе°Ҷз«ӢеҲ»еҲ йҷӨж¶үе«ҢдҫөжқғеҶ…е®№гҖӮ
жӮЁеҘҪпјҢзҷ»еҪ•еҗҺжүҚиғҪдёӢи®ўеҚ•е“ҰпјҒ