python3如何实现常见的排序算法

小编给大家分享一下python3如何实现常见的排序算法，相信大部分人都还不怎么了解，因此分享这篇文章给大家参考一下，希望大家阅读完这篇文章后大有收获，下面让我们一起去了解一下吧！

冒泡排序

冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

def mao(lst):
    for i in range(len(lst)):
        # 由于每一轮结束后，总一定有一个大的数排在后面
        # 而且后面的数已经排好了
        # 即i轮之后，就有i个数字被排好
        # 所以其 len-1 -i到 len-1的位置是已经排好的了
        # 只需要比较0到len -1 -i的位置即可

        # flag 用于标记是否刚开始就是排好的数据
        # 只有当flag状态发生改变时（第一次循环就可以确定），继续排序，否则返回
        flag = False
        for j in range(len(lst) - i - 1):
            if lst[j] > lst[j + 1]:
                lst[j], lst[j + 1] = lst[j + 1], lst[j]
                flag = True
                # 非排好的数据，改变flag
        if not flag:
            return lst
    return lst

print(mao([1, 5, 55, 4, 5, 1, 3, 4, 5, 8, 62, 7]))

选择排序

选择排序是一种简单直观的排序算法。它的工作原理：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

# 选择排序是从前开始排的
# 选择排序是从一个列表中找出一个最小的元素，然后放在第一位上。
# 冒泡排序类似
# 其 0 到 i的位置是排好的，只需要排i+1到len(lst)-1即可

def select_sort(lst):
    for i in range(len(lst)):
        min_index = i  # 用于记录最小的元素的索引
        for j in range(i + 1, len(lst)):
            if lst[j] < lst[min_index]:
                min_index = j

        # 此时，已经确定，min_index为 i+1 到len(lst) - 1 这个区间最小值的索引
        lst[i], lst[min_index] = lst[min_index], lst[i]

    return lst


def select_sort2(lst):
    # 第二种选择排序的方法
    # 原理与第一种一样
    # 不过不需要引用中间变量min_index
    # 只需要找到索引i后面的i+1到len(lst)的元素即可

    for i in range(len(lst)):
        for j in range(len(lst) - i):

            # lst[i + j]是一个i到len(lst)-1的一个数
            # 因为j <= len(lst) -i 即 j + i <= len(lst)
            if lst[i] > lst[i + j]:
                # 说明后面的数更小，更换位置
                lst[i], lst[i + j] = lst[i + j], lst[i]
    return lst


print(select_sort([1, 5, 55, 4, 5, 1, 3, 4, 5, 8, 62, 7]))
print(select_sort2([1, 5, 55, 4, 5, 1, 3, 4, 5, 8, 62, 7]))

快速排序

快速排序是通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

# 原理
# 1. 任取列表中的一个元素i
# 2. 把列表中大于i的元素放于其右边，小于则放于其左边
# 3. 如此重复
# 4. 直到不能在分，即只剩1个元素了
# 5. 然后将这些结果组合起来

def quicksort(lst):
    if len(lst) < 2:    # lst有可能为空
        return lst

    # ['pɪvət] 中心点
    pivot = lst[0]
    less_lst = [i for i in lst[1:] if i <= pivot]
    greater_lst = [i for i in lst[1:] if i > pivot]
    # 最后的结果就是
    #           左边的结果 + 中间值 + 右边的结果
    # 然后细分   左+中+右   + 中间值 + 左 + 中+ 右
    #      ...........    + 中间值 + ............
    return quicksort(less_lst) + [pivot] + quicksort(greater_lst)


print(quicksort([1, 5, 55, 4, 5, 1, 3, 4, 5, 8, 62, 7]))
print(quicksort([1, 5, 8, 62]))

插入排序

插入排序的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

# lst的[0, i) 项是有序的，因为已经排过了
# 那么只需要比对第i项的lst[i]和lst[0 : i]的元素大小即可
# 假如，lst[i]大，则不用改变位置
#     否则，lst[i]改变位置，插到j的位置，而lst[j]自然往后挪一位
#     然后再删除lst[i+1]即可（lst[i+1]是原来的lst[i]）
#
# 重复上面步骤即可，排序完成

def insert_sort(lst: list):
    # 外层开始的位置从1开始，因为从0开始都没得排
    # 只有两个元素以上才能排序
    for i in range(1, len(lst)):
        # 内层需要从0开始，因为lst[0]的位置不一定是最小的
        for j in range(i):
            if lst[i] < lst[j]:
                lst.insert(j, lst[i])
                # lst[i]已经插入到j的位置了，j之后的元素都往后+1位，所以删除lst[i+1]
                del lst[i + 1]
    return lst

print(insert_sort([1, 5, 55, 4, 5, 1, 3, 4, 5, 8, 62, 7]))

希尔排序

希尔排序是1959年Shell发明的，第一个突破O(n2)的排序算法，是简单插入排序的改进版。它与插入排序的不同之处在于，它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。

希尔排序

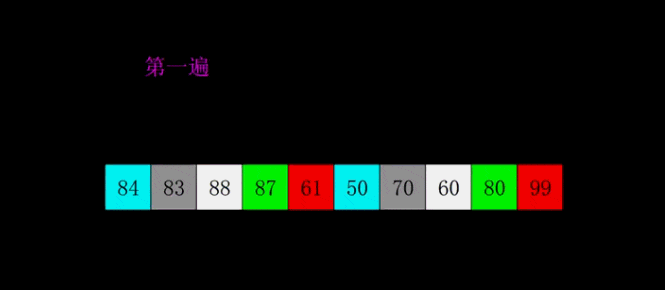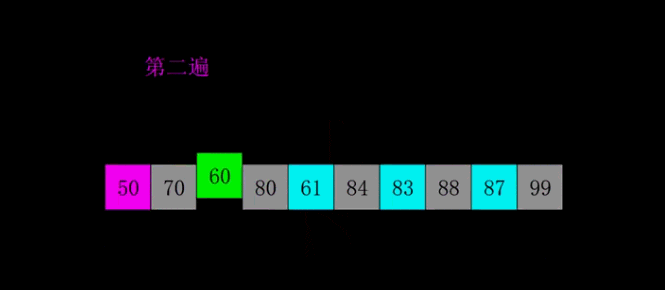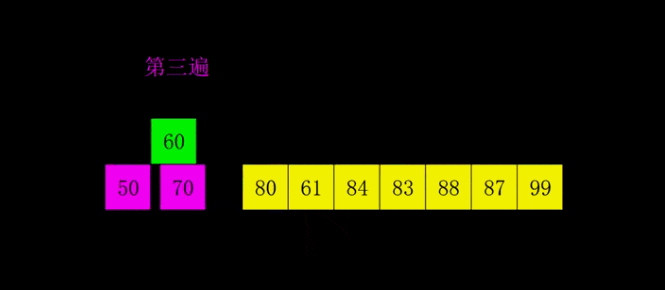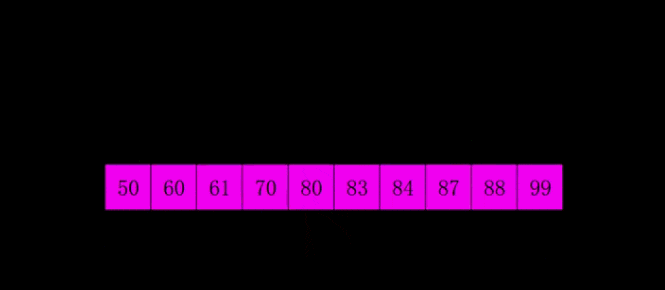
# 希尔排序是对直接插入排序的优化版本
# 1. 分组：
#       每间隔一段距离取一个元素为一组
#       间隔自己确定，一般为lst的一半
# 2. 根据插入排序，把每一组排序好
# 3. 继续分组：
#         同样没间隔一段距离取一个元素为一组
#         间隔要求比  之前的间隔少一半
# 4. 再每组插入排序
# 5. 直到间隔为1，则排序完成
#

def shell_sort(lst):
    lst_len = len(lst)
    gap = lst_len // 2  # 整除2，取间隔
    while gap >= 1:  # 间隔为0时结束
        for i in range(gap, lst_len):
            temp = lst[i]
            j = i
            # 插入排序
            while j - gap >= 0 and lst[j - gap] > temp:
                lst[j] = lst[j - gap]
                j -= gap
            lst[j] = temp
        gap //= 2
    return lst


print(shell_sort([1, 5, 55, 4, 5, 1, 3, 4, 5, 8, 62, 7]))


# 奇数
#       gap = 2
# [5, 2, 4, 3, 1]
# [5, 4, 1] [2, 3]
# [1, 4, 5, 2, 3]
#       gap = 1
# [1, 2, 3, 4, 5]

# 偶数
#       gap = 3
# [5, 2, 4, 3, 1， 6]
# [5, 3] [2, 1] [4,6]
# [3, 5, 1, 2, 4 , 6]
#       gap = 1
# [1, 2, 3, 4, 5, 6]

并归排序

归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。

并归排序

# 利用分治法
# 不断将lst分为左右两个分
# 直到不能再分
# 然后返回
# 将两边的列表的元素进行比对，排序然后返回
# 不断重复上面这一步骤
# 直到排序完成，即两个大的列表比对完成


def merge(left, right):
    # left 可能为只有一个元素的列表，或已经排好序的多个元素列表（之前调用过merge）
    # right 也一样

    res = []
    while left and right:
        item = left.pop(0) if left[0] < right[0] else right.pop(0)
        res.append(item)

    # 此时，left或right已经有一个为空，直接extend插入
    # 而且，left和right是之前已经排好序的列表，不需要再操作了

    res.extend(left)
    res.extend(right)
    return res


def merge_sort(lst):
    lst_len = len(lst)
    if lst_len <= 1:
        return lst
    mid = lst_len // 2

    lst_right = merge_sort(lst[mid:len(lst)])       # 返回的时lst_len <= 1时的 lst 或 merge中进行排序后的列表
    lst_left = merge_sort(lst[:mid])                # 返回的是lst_len <= 1时的 lst 或 merge中进行排序后的列表

    return merge(lst_left, lst_right)               # 进行排序，lst_left lst_right 的元素会不断增加


print(merge_sort([1, 5, 55, 4, 5, 1, 3, 4, 5, 8, 62, 7]))

堆排序

堆排序是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。然后进行排序。

堆排序

# 把列表创成一个大根堆或小根堆
# 然后根据大（小）根堆的特点：根节点最大（小），逐一取值
#
# 升序----使用大顶堆
#
# 降序----使用小顶堆
# 本例以小根堆为例
# 列表lst = [1, 22 ,11, 8, 12, 4, 9]

# 1. 建成一个普通的堆：
#          1
#        /   \
#       22    11
#      / \    / \
#     8  12  4   9
#
# 2. 进行调整，从子开始调整位置，要求： 父节点<= 字节点
#
#          1                                    1                                    1
#        /   \         13和22调换位置         /   \          4和11调换位置          / \
#       22    11       ==============>      13     11       ==============>       13    4
#      / \    / \                          / \    /  \                           / \   /  \
#     13  14 4   9                       22  14  4    9                        22  14 11   9
#
# 3. 取出树上根节点，即最小值，把换上叶子节点的最大值
#
#                   1
#                  /
#             ~~~~/
#          22
#         /   \
#        8     4
#         \   /  \
#         12 11   9
#
# 4. 按照同样的道理，继续形成小根堆，然后取出根节点，。。。。重复这个过程
#
#          1                    1                 1  4                1 4           1 4 8           1 4 8
#           /                    /                  /                    /             /                 /
#       ~~~/                 ~~~/               ~~~/                 ~~~/          ~~~/              ~~~/
#      22                   4                 22                   8             22                9
#     /   \               /   \              /   \               /   \          /   \             /  \
#    8     4             8     9            8     9             12    9        12    9           12  11
#     \   /  \            \   /  \           \   /               \   /              /                /
#     12 11   9           12 11  22          12 11               22 11            11               22
#
# 续上：
#       1 4 8 9          1 4 8 9           1 4 8 9 11     1 4 8 9 11    1 4 8 9 11 12   ==>  1 4 8 9 11 12 22
#            /                  /                  /                /              /
#        ~~~/               ~~~/               ~~~/             ~~~/           ~~~/
#       22                 11                22                12            22
#      /   \              /   \             /                  /
#     12    11           12    22          12                22
#
# 代码实现

def heapify(lst, lst_len, i):
    """创建一个堆"""
    less = i  # largest为最大元素的索引

    left_node_index = 2 * i + 1  # 左子节点索引
    right_node_index = 2 * i + 2  # 右子节点索引

    # lst[i] 就是父节点(假如有子节点的话)：
    #
    #                 lst[i]
    #                  /   \
    #      lst[2*i + 1]    lst[ 2*i + 2]
    #

    # 想要大根堆，即升序， 将判断左右子节点大小的 ‘>' 改为 ‘<' 即可
    #
    if left_node_index < lst_len and lst[less] > lst[left_node_index]:
        less = left_node_index

    if right_node_index < lst_len and lst[less] > lst[right_node_index]:
        # 右边节点最小的时候
        less = right_node_index

    if less != i:
        # 此时，是字节点大于父节点，所以相互交换位置
        lst[i], lst[less] = lst[less], lst[i]  # 交换
        heapify(lst, lst_len, less)
        # 节点变动了，需要再检查一下

def heap_sort(lst):
    res = []
    i = len(lst)
    lst_len = len(lst)

    for i in range(lst_len, -1, -1):
        # 要从叶节点开始比较，所以倒着来
        heapify(lst, lst_len, i)

    # 此时，已经建好了一个小根树
    # 所以，交换元素，将根节点（最小值）放在后面，重复这个过程
    for j in range(lst_len - 1, 0, -1):
        lst[0], lst[j] = lst[j], lst[0]  # 交换，最小的放在j的位置

        heapify(lst, j, 0)      # 再次构建一个[0: j)小根堆 [j: lst_len-1]已经倒序排好了
    return lst

arr = [1, 5, 55, 4, 5, 1, 3, 4, 5, 8, 62, 7]
print(heap_sort(arr))

以上是“python3如何实现常见的排序算法”这篇文章的所有内容，感谢各位的阅读！相信大家都有了一定的了解，希望分享的内容对大家有所帮助，如果还想学习更多知识，欢迎关注亿速云行业资讯频道！