您好,登录后才能下订单哦!
这篇文章主要介绍了Python中Sklearn库如何使用,具有一定借鉴价值,感兴趣的朋友可以参考下,希望大家阅读完这篇文章之后大有收获,下面让小编带着大家一起了解一下。
Python sklearn库是一个丰富的机器学习库,里面包含内容太多,这里对一些工程里常用的操作做个简要的概述,以后还会根据自己用的进行更新。
简单来说 LabelEncoder 是对不连续的数字或者文本进行按序编号,可以用来生成属性/标签
from sklearn.preprocessing import LabelEncoder encoder=LabelEncoder() encoder.fit([1,3,2,6]) t=encoder.transform([1,6,6,2]) print(t)
输出: [0 3 3 1]
OneHotEncoder 用于将表示分类的数据扩维,将[[1],[2],[3],[4]]映射为 0,1,2,3的位置为1(高维的数据自己可以测试):
from sklearn.preprocessing import OneHotEncoder oneHot=OneHotEncoder()#声明一个编码器 oneHot.fit([[1],[2],[3],[4]]) print(oneHot.transform([[2],[3],[1],[4]]).toarray())
输出:[[0. 1. 0. 0.]
[0. 0. 1. 0.]
[1. 0. 0. 0.]
[0. 0. 0. 1.]]
正如keras中的keras.utils.to_categorical(y_train, num_classes)
一般形式:
train_test_split是交叉验证中常用的函数,功能是从样本中随机的按比例选取train data和testdata,形式为:
X_train,X_test, y_train, y_test =train_test_split(train_data,train_target,test_size=0.2, train_size=0.8,random_state=0)
参数解释:
- train_data:所要划分的样本特征集
- train_target:所要划分的样本结果
- test_size:测试样本占比,如果是整数的话就是样本的数量
-train_size:训练样本的占比,(注:测试占比和训练占比任写一个就行)
- random_state:是随机数的种子。
- 随机数种子:其实就是该组随机数的编号,在需要重复试验的时候,保证得到一组一样的随机数。比如你每次都填1,其他参数一样的情况下你得到的随机数组是一样的。但填0或不填,每次都会不一样。
随机数的产生取决于种子,随机数和种子之间的关系遵从以下两个规则:
- 种子不同,产生不同的随机数;种子相同,即使实例不同也产生相同的随机数。
from sklearn.model_selection import train_test_split from sklearn.datasets import load_iris iris=load_iris() train=iris.data target=iris.target # 避免过拟合,采用交叉验证,验证集占训练集20%,固定随机种子(random_state) train_X,test_X, train_y, test_y = train_test_split(train, target, test_size = 0.2, random_state = 0) print(train_y.shape)
得到的结果数据:train_X : 训练集的数据,train_Y:训练集的标签,对应test 为测试集的数据和标签
本节参考与文章:用 Pipeline 将训练集参数重复应用到测试集
pipeline 实现了对全部步骤的流式化封装和管理,可以很方便地使参数集在新数据集上被重复使用。
pipeline 可以用于下面几处:
模块化 Feature Transform,只需写很少的代码就能将新的 Feature 更新到训练集中。
自动化 Grid Search,只要预先设定好使用的 Model 和参数的候选,就能自动搜索并记录最佳的 Model。
自动化 Ensemble Generation,每隔一段时间将现有最好的 K 个 Model 拿来做 Ensemble。
问题是要对数据集 Breast Cancer Wisconsin 进行分类,
该数据集包含 569 个样本,第一列 ID,第二列类别(M=恶性肿瘤,B=良性肿瘤),
第 3-32 列是实数值的特征。
我们要用 Pipeline 对训练集和测试集进行如下操作:
先用 StandardScaler 对数据集每一列做标准化处理,(是 transformer)
再用 PCA 将原始的 30 维度特征压缩的 2 维度,(是 transformer)
最后再用模型 LogisticRegression。(是 Estimator)
调用 Pipeline 时,输入由元组构成的列表,每个元组第一个值为变量名,元组第二个元素是 sklearn 中的 transformer
或 Estimator。
注意中间每一步是 transformer,即它们必须包含 fit 和 transform 方法,或者 fit_transform。
最后一步是一个 Estimator,即最后一步模型要有 fit 方法,可以没有 transform 方法。
然后用 Pipeline.fit对训练集进行训练,pipe_lr.fit(X_train, y_train)
再直接用 Pipeline.score 对测试集进行预测并评分 pipe_lr.score(X_test, y_test)
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
#需要联网
df = pd.read_csv('http://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/wdbc.data',
header=None)
# Breast Cancer Wisconsin dataset
X, y = df.values[:, 2:], df.values[:, 1]
encoder = LabelEncoder()
y = encoder.fit_transform(y)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.2, random_state=0)
pipe_lr = Pipeline([('sc', StandardScaler()),
('pca', PCA(n_components=2)),
('clf', LogisticRegression(random_state=1))
])
pipe_lr.fit(X_train, y_train)
print('Test accuracy: %.3f' % pipe_lr.score(X_test, y_test))还可以用来选择特征:
例如用 SelectKBest 选择特征,
分类器为 SVM,
anova_filter = SelectKBest(f_regression, k=5)
clf = svm.SVC(kernel='linear')
anova_svm = Pipeline([('anova', anova_filter), ('svc', clf)])当然也可以应用 K-fold cross validation:
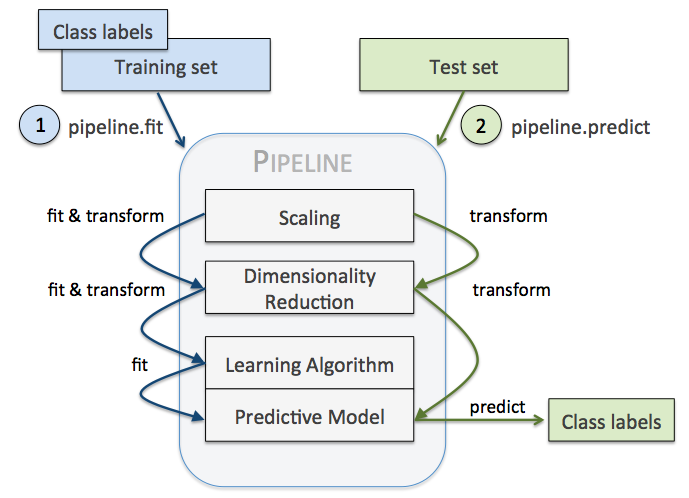
Pipeline 的工作方式:
当管道 Pipeline 执行 fit 方法时,
首先 StandardScaler 执行 fit 和 transform 方法,
然后将转换后的数据输入给 PCA,
PCA 同样执行 fit 和 transform 方法,
再将数据输入给 LogisticRegression,进行训练。
predict_proba返回每组数据预测值的概率,每行的概率和为1,如训练集/测试集有 下例中的两个类别,测试集有三个,则 predict返回的是一个 3*1的向量,而 predict_proba 返回的是 3*2维的向量,如下结果所示。
# conding :utf-8 from sklearn.linear_model import LogisticRegression import numpy as np x_train = np.array([[1, 2, 3], [1, 3, 4], [2, 1, 2], [4, 5, 6], [3, 5, 3], [1, 7, 2]]) y_train = np.array([3, 3, 3, 2, 2, 2]) x_test = np.array([[2, 2, 2], [3, 2, 6], [1, 7, 4]]) clf = LogisticRegression() clf.fit(x_train, y_train) # 返回预测标签 print(clf.predict(x_test)) # 返回预测属于某标签的概率 print(clf.predict_proba(x_test))

1. sklearn.metrics.roc_curve(true_y. pred_proba_score, pos_labal)
计算roc曲线,roc曲线有三个属性:fpr, tpr,和阈值,因此该函数返回这三个变量,l
2. sklearn.metrics.auc(x, y, reorder=False):
计算AUC值,其中x,y分别为数组形式,根据(xi, yi)在坐标上的点,生成的曲线,然后计算AUC值;
import numpy as np from sklearn.metrics import roc_curve from sklearn.metrics import auc y = np.array([1,0,2,2]) pred = np.array([0.1, 0.4, 0.35, 0.8]) fpr, tpr, thresholds = roc_curve(y, pred, pos_label=2) print(tpr) print(fpr) print(thresholds) print(auc(fpr, tpr))
3. sklearn.metrics.roc_auc_score(true_y, pred_proba_y)
直接根据真实值(必须是二值)、预测值(可以是0/1, 也可以是proba值)计算出auc值,中间过程的roc计算省略
GridSearchCV,它存在的意义就是自动调参,只要把参数输进去,就能给出最优化的结果和参数。但是这个方法适合于小数据集,一旦数据的量级上去了,很难得出结果。这个时候就是需要动脑筋了。数据量比较大的时候可以使用一个快速调优的方法——坐标下降。它其实是一种贪心算法:拿当前对模型影响最大的参数调优,直到最优化;再拿下一个影响最大的参数调优,如此下去,直到所有的参数调整完毕。这个方法的缺点就是可能会调到局部最优而不是全局最优,但是省时间省力,巨大的优势面前,还是试一试吧,后续可以再拿bagging再优化。
回到sklearn里面的GridSearchCV,GridSearchCV用于系统地遍历多种参数组合,通过交叉验证确定最佳效果参数。
GridSearchCV的sklearn官方网址:http://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GridSearchCV.html#sklearn.model_selection.GridSearchCV
classsklearn.model_selection.GridSearchCV(estimator,param_grid, scoring=None, fit_params=None, n_jobs=1, iid=True, refit=True,cv=None, verbose=0, pre_dispatch='2*n_jobs', error_score='raise',return_train_score=True)
常用参数解读
estimator:所使用的分类器,如estimator=RandomForestClassifier(min_samples_split=100,min_samples_leaf=20,max_depth=8,max_features='sqrt',random_state=10), 并且传入除需要确定最佳的参数之外的其他参数。每一个分类器都需要一个scoring参数,或者score方法。
param_grid:值为字典或者列表,即需要最优化的参数的取值,param_grid =param_test1,param_test1 = {'n_estimators':range(10,71,10)}。
scoring :准确度评价标准,默认None,这时需要使用score函数;或者如scoring='roc_auc',根据所选模型不同,评价准则不同。字符串(函数名),或是可调用对象,需要其函数签名形如:scorer(estimator, X, y);如果是None,则使用estimator的误差估计函数。
cv :交叉验证参数,默认None,使用三折交叉验证。指定fold数量,默认为3,也可以是yield训练/测试数据的生成器。
refit :默认为True,程序将会以交叉验证训练集得到的最佳参数,重新对所有可用的训练集与开发集进行,作为最终用于性能评估的最佳模型参数。即在搜索参数结束后,用最佳参数结果再次fit一遍全部数据集。
iid:默认True,为True时,默认为各个样本fold概率分布一致,误差估计为所有样本之和,而非各个fold的平均。
verbose:日志冗长度,int:冗长度,0:不输出训练过程,1:偶尔输出,>1:对每个子模型都输出。
n_jobs: 并行数,int:个数,-1:跟CPU核数一致, 1:默认值。
pre_dispatch:指定总共分发的并行任务数。当n_jobs大于1时,数据将在每个运行点进行复制,这可能导致OOM,而设置pre_dispatch参数,则可以预先划分总共的job数量,使数据最多被复制pre_dispatch次
进行预测的常用方法和属性
grid.fit():运行网格搜索
grid_scores_:给出不同参数情况下的评价结果
best_params_:描述了已取得最佳结果的参数的组合
best_score_:成员提供优化过程期间观察到的最好的评分
model=Lasso()
alpha_can=np.logspace(-3,2,10)
np.set_printoptions(suppress=True)#设置打印选项
print("alpha_can=",alpha_can)
#cv :交叉验证参数,默认None 这里为5折交叉
# param_grid:值为字典或者列表,即需要最优化的参数的取值
lasso_model=GridSearchCV(model,param_grid={'alpha':alpha_can},cv=5)#得到最好的参数
lasso_model.fit(x_train,y_train)
print('超参数:\n',lasso_model.best_params_)
print("估计器\n",lasso_model.best_estimator_)
如果有transform,使用Pipeline简化系统搭建流程,将transform与分类器串联起来(Pipelineof transforms with a final estimator)
pipeline= Pipeline([("features", combined_features), ("svm", svm)])
param_grid= dict(features__pca__n_components=[1, 2, 3],
features__univ_select__k=[1,2],
svm__C=[0.1, 1, 10])
grid_search= GridSearchCV(pipeline, param_grid=param_grid, verbose=10)
grid_search.fit(X,y)
print(grid_search.best_estimator_)作用:去均值和方差归一化。且是针对每一个特征维度来做的,而不是针对样本。
【注意:】
并不是所有的标准化都能给estimator带来好处。
# coding=utf-8
# 统计训练集的 mean 和 std 信息
from sklearn.preprocessing import StandardScaler
import numpy as np
def test_algorithm():
np.random.seed(123)
print('use StandardScaler')
# 注:shape of data: [n_samples, n_features]
data = np.random.randn(3, 4)
scaler = StandardScaler()
scaler.fit(data)
trans_data = scaler.transform(data)
print('original data: ')
print(data)
print('transformed data: ')
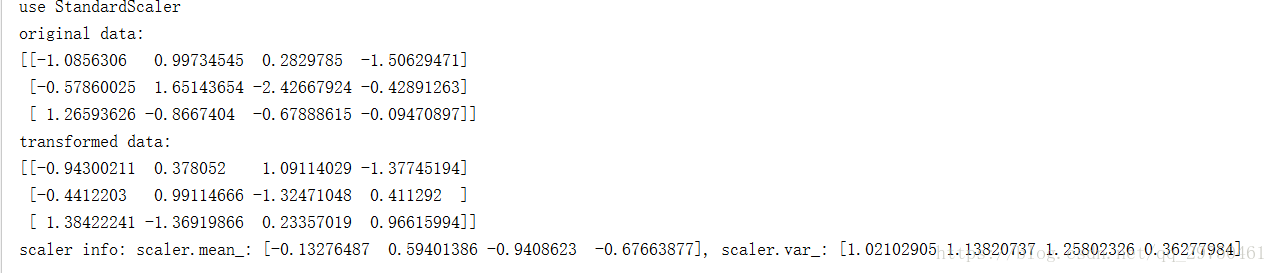
print(trans_data)
print('scaler info: scaler.mean_: {}, scaler.var_: {}'.format(scaler.mean_, scaler.var_))
print('\n')
print('use numpy by self')
mean = np.mean(data, axis=0)
std = np.std(data, axis=0)
var = std * std
print('mean: {}, std: {}, var: {}'.format(mean, std, var))
# numpy 的广播功能
another_trans_data = data - mean
# 注:是除以标准差
another_trans_data = another_trans_data / std
print('another_trans_data: ')
print(another_trans_data)
if __name__ == '__main__':
test_algorithm()运行结果:

使用sklearn.preprocessing.PolynomialFeatures来进行特征的构造。
它是使用多项式的方法来进行的,如果有a,b两个特征,那么它的2次多项式为(1,a,b,a^2,ab, b^2)。
PolynomialFeatures有三个参数
degree:控制多项式的度
interaction_only: 默认为False,如果指定为True,那么就不会有特征自己和自己结合的项,上面的二次项中没有a^2和b^2。
include_bias:默认为True。如果为True的话,那么就会有上面的 1那一项。
import pandas as pd
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.pipeline import Pipeline
path = r"activity_recognizer\1.csv"
# 数据在https://archive.ics.uci.edu/ml/datasets/Activity+Recognition+from+Single+Chest-Mounted+Accelerometer
df = pd.read_csv(path, header=None)
df.columns = ['index', 'x', 'y', 'z', 'activity']
knn = KNeighborsClassifier()
knn_params = {'n_neighbors': [3, 4, 5, 6]}
X = df[['x', 'y', 'z']]
y = df['activity']
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=2, include_bias=False, interaction_only=False)
X_ploly = poly.fit_transform(X)
X_ploly_df = pd.DataFrame(X_ploly, columns=poly.get_feature_names())
print(X_ploly_df.head())运行结果:
x0 x1 x2 x0^2 x0 x1 x0 x2 x1^2 \
0 1502.0 2215.0 2153.0 2256004.0 3326930.0 3233806.0 4906225.0
1 1667.0 2072.0 2047.0 2778889.0 3454024.0 3412349.0 4293184.0
2 1611.0 1957.0 1906.0 2595321.0 3152727.0 3070566.0 3829849.0
3 1601.0 1939.0 1831.0 2563201.0 3104339.0 2931431.0 3759721.0
4 1643.0 1965.0 1879.0 2699449.0 3228495.0 3087197.0 3861225.0
x1 x2 x2^2
0 4768895.0 4635409.0
1 4241384.0 4190209.0
2 3730042.0 3632836.0
3 3550309.0 3352561.0
4 3692235.0 3530641.0
Sklearn API:http://scikit-learn.org/stable/modules/classes.html#module-sklearn.ensemble
import numpy as np
np.random.seed(10)
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import (RandomTreesEmbedding, RandomForestClassifier,
GradientBoostingClassifier)
from sklearn.preprocessing import OneHotEncoder
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_curve,accuracy_score,recall_score
from sklearn.pipeline import make_pipeline
from sklearn.calibration import calibration_curve
import copy
print(__doc__)
from matplotlib.colors import ListedColormap
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_moons, make_circles, make_classification
from sklearn.neural_network import MLPClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.gaussian_process.kernels import RBF
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
# 数据
X, y = make_classification(n_samples=100000)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,random_state = 4000) # 对半分
X_train, X_train_lr, y_train, y_train_lr = train_test_split(X_train,
y_train,
test_size=0.2,random_state = 4000)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)
def yLabel(y_pred):
y_pred_f = copy.copy(y_pred)
y_pred_f[y_pred_f>=0.5] = 1
y_pred_f[y_pred_f<0.5] = 0
return y_pred_f
def acc_recall(y_test, y_pred_rf):
return {'accuracy': accuracy_score(y_test, yLabel(y_pred_rf)), \
'recall': recall_score(y_test, yLabel(y_pred_rf))}h = .02 # step size in the mesh
names = ["Nearest Neighbors", "Linear SVM", "RBF SVM",
"Decision Tree", "Neural Net", "AdaBoost",
"Naive Bayes", "QDA"]
# 去掉"Gaussian Process",太耗时,是其他的300倍以上
classifiers = [
KNeighborsClassifier(3),
SVC(kernel="linear", C=0.025),
SVC(gamma=2, C=1),
#GaussianProcessClassifier(1.0 * RBF(1.0)),
DecisionTreeClassifier(max_depth=5),
#RandomForestClassifier(max_depth=5, n_estimators=10, max_features=1),
MLPClassifier(alpha=1),
AdaBoostClassifier(),
GaussianNB(),
QuadraticDiscriminantAnalysis()]
predictEight = {}
for name, clf in zip(names, classifiers):
predictEight[name] = {}
predictEight[name]['prob_pos'],predictEight[name]['fpr_tpr'],predictEight[name]['acc_recall'] = [],[],[]
predictEight[name]['importance'] = []
print('\n --- Start Model : %s ----\n'%name)
%time clf.fit(X_train, y_train)
# 一些计算决策边界的模型 计算decision_function
if hasattr(clf, "decision_function"):
%time prob_pos = clf.decision_function(X_test)
# # The confidence score for a sample is the signed distance of that sample to the hyperplane.
else:
%time prob_pos= clf.predict_proba(X_test)[:, 1]
prob_pos = (prob_pos - prob_pos.min()) / (prob_pos.max() - prob_pos.min())
# 需要归一化
predictEight[name]['prob_pos'] = prob_pos
# 计算ROC、acc、recall
predictEight[name]['fpr_tpr'] = roc_curve(y_test, prob_pos)[:2]
predictEight[name]['acc_recall'] = acc_recall(y_test, prob_pos) # 计算准确率与召回
# 提取信息
if hasattr(clf, "coef_"):
predictEight[name]['importance'] = clf.coef_
elif hasattr(clf, "feature_importances_"):
predictEight[name]['importance'] = clf.feature_importances_
elif hasattr(clf, "sigma_"):
predictEight[name]['importance'] = clf.sigma_
# variance of each feature per class 在朴素贝叶斯之中体现结果输出类似:
Automatically created module for IPython interactive environment
--- Start Model : Nearest Neighbors ----
CPU times: user 103 ms, sys: 0 ns, total: 103 ms
Wall time: 103 ms
CPU times: user 2min 8s, sys: 3.43 ms, total: 2min 8s
Wall time: 2min 9s
--- Start Model : Linear SVM ----
CPU times: user 25.4 s, sys: 149 ms, total: 25.6 s
Wall time: 25.6 s
CPU times: user 3.47 s, sys: 1.23 ms, total: 3.47 s
Wall time: 3.47 s
案例地址:http://scikit-learn.org/stable/auto_examples/ensemble/plot_feature_transformation.html#sphx-glr-auto-examples-ensemble-plot-feature-transformation-py
'''
model 0 : lm
logistic
'''
print('LM 开始计算...')
lm = LogisticRegression()
%time lm.fit(X_train, y_train)
y_pred_lm = lm.predict_proba(X_test)[:, 1]
fpr_lm, tpr_lm, _ = roc_curve(y_test, y_pred_lm)
lm_ar = acc_recall(y_test, y_pred_lm) # 计算准确率与召回
'''
model 1 : rt + lm
无监督变换 + lg
'''
# Unsupervised transformation based on totally random trees
print('随机森林编码+LM 开始计算...')
rt = RandomTreesEmbedding(max_depth=3, n_estimators=n_estimator,
random_state=0)
# 数据集的无监督变换到高维稀疏表示。
rt_lm = LogisticRegression()
pipeline = make_pipeline(rt, rt_lm)
%time pipeline.fit(X_train, y_train)
y_pred_rt = pipeline.predict_proba(X_test)[:, 1]
fpr_rt_lm, tpr_rt_lm, _ = roc_curve(y_test, y_pred_rt)
rt_lm_ar = acc_recall(y_test, y_pred_rt) # 计算准确率与召回
'''
model 2 : RF / RF+LM
'''
print('\n 随机森林系列 开始计算... ')
# Supervised transformation based on random forests
rf = RandomForestClassifier(max_depth=3, n_estimators=n_estimator)
rf_enc = OneHotEncoder()
rf_lm = LogisticRegression()
rf.fit(X_train, y_train)
rf_enc.fit(rf.apply(X_train)) # rf.apply(X_train)-(1310, 100) X_train-(1310, 20)
# 用100棵树的信息作为X,载入做LM模型
%time rf_lm.fit(rf_enc.transform(rf.apply(X_train_lr)), y_train_lr)
y_pred_rf_lm = rf_lm.predict_proba(rf_enc.transform(rf.apply(X_test)))[:, 1]
fpr_rf_lm, tpr_rf_lm, _ = roc_curve(y_test, y_pred_rf_lm)
rf_lm_ar = acc_recall(y_test, y_pred_rf_lm) # 计算准确率与召回
'''
model 2 : GRD / GRD + LM
'''
print('\n 梯度提升树系列 开始计算... ')
grd = GradientBoostingClassifier(n_estimators=n_estimator)
grd_enc = OneHotEncoder()
grd_lm = LogisticRegression()
grd.fit(X_train, y_train)
grd_enc.fit(grd.apply(X_train)[:, :, 0])
%time grd_lm.fit(grd_enc.transform(grd.apply(X_train_lr)[:, :, 0]), y_train_lr)
y_pred_grd_lm = grd_lm.predict_proba(
grd_enc.transform(grd.apply(X_test)[:, :, 0]))[:, 1]
fpr_grd_lm, tpr_grd_lm, _ = roc_curve(y_test, y_pred_grd_lm)
grd_lm_ar = acc_recall(y_test, y_pred_grd_lm) # 计算准确率与召回
# The gradient boosted model by itself
y_pred_grd = grd.predict_proba(X_test)[:, 1]
fpr_grd, tpr_grd, _ = roc_curve(y_test, y_pred_grd)
grd_ar = acc_recall(y_test, y_pred_grd) # 计算准确率与召回
# The random forest model by itself
y_pred_rf = rf.predict_proba(X_test)[:, 1]
fpr_rf, tpr_rf, _ = roc_curve(y_test, y_pred_rf)
rf_ar = acc_recall(y_test, y_pred_rf) # 计算准确率与召回输出结果为:
LM 开始计算...
随机森林编码+LM 开始计算...
CPU times: user 591 ms, sys: 85.5 ms, total: 677 ms
Wall time: 574 ms
随机森林系列 开始计算...
CPU times: user 76 ms, sys: 0 ns, total: 76 ms
Wall time: 76 ms
梯度提升树系列 开始计算...
CPU times: user 60.6 ms, sys: 0 ns, total: 60.6 ms
Wall time: 60.6 ms
# 8款常规模型
for x,y in predictEight.items():
print('\n ----- The Model : %s , -----\n '%(x) )
print(predictEight[x]['acc_recall'])
# 树模型
names = ['LM','LM + RT','LM + RF','GBT + LM','GBT','RF']
ar_list = [lm_ar,rt_lm_ar,rf_lm_ar,grd_lm_ar,grd_ar,rf_ar]
for x,y in zip(names,ar_list):
print('\n --- %s 准确率与召回为: ---- \n '%x,y)结果输出:
----- The Model : Linear SVM , -----
{'recall': 0.84561049445005043, 'accuracy': 0.89100000000000001}
---- The Model : Decision Tree , -----
{'recall': 0.90918264379414737, 'accuracy': 0.89949999999999997}
----- The Model : AdaBoost , -----
{'recall': 0.028254288597376387, 'accuracy': 0.51800000000000002}
----- The Model : Neural Net , -----
{'recall': 0.91523713420787078, 'accuracy': 0.90249999999999997}
----- The Model : Naive Bayes , -----
{'recall': 0.91523713420787078, 'accuracy': 0.89300000000000002}
Calibration curves may also be referred to as reliability diagrams.
可靠性检验的方式。
# #############################################################################
# Plot calibration plots
names = ["Nearest Neighbors", "Linear SVM", "RBF SVM",
"Decision Tree", "Neural Net", "AdaBoost",
"Naive Bayes", "QDA"]
plt.figure(figsize=(15, 15))
ax1 = plt.subplot2grid((3, 1), (0, 0), rowspan=2)
ax2 = plt.subplot2grid((3, 1), (2, 0))
ax1.plot([0, 1], [0, 1], "k:", label="Perfectly calibrated")
for prob_pos, name in [[predictEight[n]['prob_pos'],n] for n in names] + [(y_pred_lm,'LM'),
(y_pred_rt,'RT + LM'),
(y_pred_rf_lm,'RF + LM'),
(y_pred_grd_lm,'GBT + LM'),
(y_pred_grd,'GBT'),
(y_pred_rf,'RF')]:
prob_pos = (prob_pos - prob_pos.min()) / (prob_pos.max() - prob_pos.min())
fraction_of_positives, mean_predicted_value = calibration_curve(y_test, prob_pos, n_bins=10)
ax1.plot(mean_predicted_value, fraction_of_positives, "s-",
label="%s" % (name, ))
ax2.hist(prob_pos, range=(0, 1), bins=10, label=name,
histtype="step", lw=2)
ax1.set_ylabel("Fraction of positives")
ax1.set_ylim([-0.05, 1.05])
ax1.legend(loc="lower right")
ax1.set_title('Calibration plots (reliability curve)')
ax2.set_xlabel("Mean predicted value")
ax2.set_ylabel("Count")
ax2.legend(loc="upper center", ncol=2)
plt.tight_layout()
plt.show()第一张图
fraction_of_positives,每个概率片段,正数的比例= 正数/总数
Mean predicted value,每个概率片段,正数的平均值
第二张图
每个概率分数段的个数
结果展示为:


大家都知道一些树模型可以输出重要性,回归模型可以输出系数,带有决策平面的(譬如SVM)可以计算点到决策边界的距离。
# 重要性
print('\n -------- RadomFree importances ------------\n')
print(rf.feature_importances_)
print('\n -------- GradientBoosting importances ------------\n')
print(grd.feature_importances_)
print('\n -------- Logistic Coefficient ------------\n')
lm.coef_
# 其他几款模型的特征选择
[[predictEight[n]['importance'],n] for n in names if predictEight[n]['importance'] != [] ]在本次10+机器学习案例之中,可以看到,可以输出重要性的模型有:
随机森林rf.feature_importances_
GBTgrd.feature_importances_
Decision Tree decision.feature_importances_
AdaBoost AdaBoost.feature_importances_
可以计算系数的有:线性模型,lm.coef_ 、 SVM svm.coef_
Naive Bayes得到的是:NaiveBayes.sigma_
解释为:variance of each feature per class
plt.figure(1)
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr_lm, tpr_lm, label='LR')
plt.plot(fpr_rt_lm, tpr_rt_lm, label='RT + LR')
plt.plot(fpr_rf, tpr_rf, label='RF')
plt.plot(fpr_rf_lm, tpr_rf_lm, label='RF + LR')
plt.plot(fpr_grd, tpr_grd, label='GBT')
plt.plot(fpr_grd_lm, tpr_grd_lm, label='GBT + LR')
# 8 款模型
for (fpr,tpr),name in [[predictEight[n]['fpr_tpr'],n] for n in names] :
plt.plot(fpr, tpr, label=name)
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title('ROC curve')
plt.legend(loc='best')
plt.show()
plt.figure(2)
plt.xlim(0, 0.2)
plt.ylim(0.4, 1) # ylim改变 # matt
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr_lm, tpr_lm, label='LR')
plt.plot(fpr_rt_lm, tpr_rt_lm, label='RT + LR')
plt.plot(fpr_rf, tpr_rf, label='RF')
plt.plot(fpr_rf_lm, tpr_rf_lm, label='RF + LR')
plt.plot(fpr_grd, tpr_grd, label='GBT')
plt.plot(fpr_grd_lm, tpr_grd_lm, label='GBT + LR')
for (fpr,tpr),name in [[predictEight[n]['fpr_tpr'],n] for n in names] :
plt.plot(fpr, tpr, label=name)
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title('ROC curve (zoomed in at top left)')
plt.legend(loc='best')
plt.show()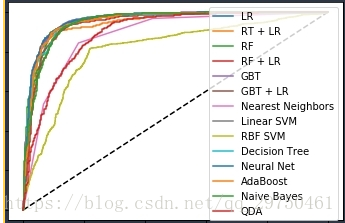

感谢你能够认真阅读完这篇文章,希望小编分享的“Python中Sklearn库如何使用”这篇文章对大家有帮助,同时也希望大家多多支持亿速云,关注亿速云行业资讯频道,更多相关知识等着你来学习!
免责声明:本站发布的内容(图片、视频和文字)以原创、转载和分享为主,文章观点不代表本网站立场,如果涉及侵权请联系站长邮箱:is@yisu.com进行举报,并提供相关证据,一经查实,将立刻删除涉嫌侵权内容。