JavaScript网格中的最小路径怎么实现

这篇“JavaScript网格中的最小路径怎么实现”文章的知识点大部分人都不太理解，所以小编给大家总结了以下内容，内容详细，步骤清晰，具有一定的借鉴价值，希望大家阅读完这篇文章能有所收获，下面我们一起来看看这篇“JavaScript网格中的最小路径怎么实现”文章吧。

问题描述

给你一个下标从 0 开始的整数矩阵 grid ，矩阵大小为 m x n ，由从 0 到 m * n - 1 的不同整数组成。你可以在此矩阵中，从一个单元格移动到 下一行 的任何其他单元格。如果你位于单元格 (x, y) ，且满足 x < m - 1 ，你可以移动到 (x + 1, 0), (x + 1, 1), ..., (x + 1, n - 1) 中的任何一个单元格。注意： 在最后一行中的单元格不能触发移动。

每次可能的移动都需要付出对应的代价，代价用一个下标从 0 开始的二维数组 moveCost 表示，该数组大小为 (m * n) x n ，其中 moveCost[i][j] 是从值为 i 的单元格移动到下一行第 j 列单元格的代价。从 grid 最后一行的单元格移动的代价可以忽略。

grid 一条路径的代价是：所有路径经过的单元格的 值之和 加上 所有移动的 代价之和 。从 第一行 任意单元格出发，返回到达 最后一行 任意单元格的最小路径代价。

示例 1：

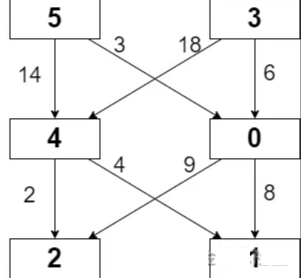
输入：grid = [[5,3],[4,0],[2,1]], moveCost = [[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]]
输出：17
解释：最小代价的路径是 5 -> 0 -> 1 。
- 路径途经单元格值之和 5 + 0 + 1 = 6 。
- 从 5 移动到 0 的代价为 3 。
- 从 0 移动到 1 的代价为 8 。
路径总代价为 6 + 3 + 8 = 17 。

示例 2：

输入：grid = [[5,1,2],[4,0,3]], moveCost = [[12,10,15],[20,23,8],[21,7,1],[8,1,13],[9,10,25],[5,3,2]]
输出：6
解释：
最小代价的路径是 2 -> 3 。 
- 路径途经单元格值之和 2 + 3 = 5 。 
- 从 2 移动到 3 的代价为 1 。 
路径总代价为 5 + 1 = 6 。

提示：

m == grid.length
n == grid[i].length
2 <= m, n <= 50
grid 由从 0 到 m * n - 1 的不同整数组成
moveCost.length == m * n
moveCost[i].length == n
1 <= moveCost[i][j] <= 100

思路分析

这道题目其实并不难，难的是对于题目的理解，题目有点长和绕，我们需要仔细阅读清楚题目给的信息，结合示例一的图片进行理解会更清晰。

1、题目会给出一个 m * n 的矩阵；

一个下标从 0 开始的整数矩阵 grid ，矩阵大小为 m x n ，由从 0 到 m * n - 1 的不同整数组成。

2、每一行的格子可以移动到下一行的任意一格；

在此矩阵中，从一个单元格移动到 下一行 的任何其他单元格。如果你位于单元格 (x, y) ，且满足 x < m - 1 ，你可以移动到 (x + 1, 0), (x + 1, 1), ..., (x + 1, n - 1) 中的任何一个单元格。

3、moveCost[i][j]表示从值为 i 的单元格移动到下一行第 j 列单元格的代价

每次可能的移动都需要付出对应的代价，代价用一个下标从 0 开始的二维数组 moveCost 表示，该数组大小为 (m * n) x n ，其中 moveCost[i][j] 是从值为 i 的单元格移动到下一行第 j 列单元格的代价。

4、求从 第一行 任意单元格出发，返回到达 最后一行 任意单元格的最小路径代价。

grid 一条路径的代价是：所有路径经过的单元格的 值之和 加上 所有移动的 代价之和 。从 第一行 任意单元格出发，返回到达 最后一行 任意单元格的最小路径代价。

理清楚上面的这四个信息之后，我们可以发现这是一道经典的dp动态规划的题目,我们每一个格子的上一步只能是上一行的某一格，我们只需要自顶向下求出移动到每一个格子的最下代价即可。

遍历矩阵的每一个格子，维护上一行到当前格子的最小代价，最后求出最后一行的格子的最小代价即可。

AC代码

/**
 * @param {number[][]} grid
 * @param {number[][]} moveCost
 * @return {number}
 */
 var minPathCost = function(grid, moveCost) {
    let dp = new Array(grid.length);
    let res = Infinity;
    for(let i = 0; i < dp.length; i++){
        dp[i] = new Array(grid[i].length).fill(0);
        for(let j = 0; j <  dp[i].length; j++){
            if(i === 0) dp[i][j] = grid[i][j];
            else{
                let temp = Infinity;
                for(let k = 0; k < dp[i].length; k++){
                    temp = Math.min(temp,dp[i - 1][k] + moveCost[grid[i - 1][k]][j]);
                }
                dp[i][j] = temp + grid[i][j];
            }
            if(i == grid.length - 1){
                res = Math.min(dp[i][j],res);
            }
        }
    }
    return res;
};

以上就是关于“JavaScript网格中的最小路径怎么实现”这篇文章的内容，相信大家都有了一定的了解，希望小编分享的内容对大家有帮助，若想了解更多相关的知识内容，请关注亿速云行业资讯频道。