您好,登录后才能下订单哦!
密码登录
登录注册
点击 登录注册 即表示同意《亿速云用户服务条款》
1 、Prim算法思想
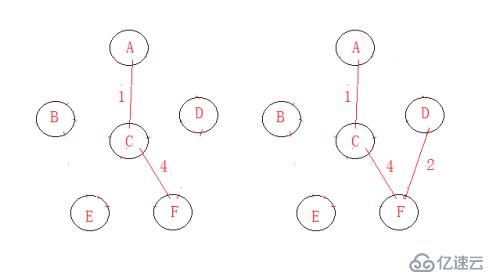
思想:首先找到权值最小的一条边,由这两个顶点出发,分别去找权值最小的(不能有环的出现);由各个顶点,每次都找权值最小的。
连贯的做法:从顶点的连续角度出发,每次从相应顶点出发,到权值最小的边进行连接。
模型如下:


2、Prim算法实现
lowCost[i]:表示以i为终点的边的最小权值,当lowCost[i] = 0;说明以i为终点的边的最小权值=0;也就是表示i点加入了mst数组;
mst[i]:表示对应lowCost[i]的起点,即说明边<mst[i], i>是mst的一条边;
每次进行一次比较,都要随之更改其lowCost和mst数组;
每并入一个顶点,都更改为0,并且修改相应的记录;都会从内部挑选最小的权值,直到最后所有的lowCost[i] = 0;
均由C++实现(邻接矩阵实现):
template<typename Type, typename E>
void GraphMtx<Type, E>::MinSpanTree_Prim(const Type &v){
int n = Graph<Type, E>::getCurVertex();
int *lowCost = new int[n]; //这两个数组是至关重要的
int *mst = new int[n];
int k = getVertexIndex(v);
for(int i = 0; i < n; i++){
if(i != k){
lowCost[i] = edge[k][i]; //i:表示最终顶点,lowCost[i]:表示起始到最终顶点的权值;
mst[i] = k; //起始顶点
}else{
lowCost[i] = 0;
}
}
int min;
int minIndex;
int begin;
int end;
for(i = 0; i < n-1; i++){
min = MAX_COST;
minIndex = -1;
for(int j = 0; j < n; j++){
if(lowCost[j] != 0 && lowCost[j] < min){
min = lowCost[j]; //最小权值
minIndex = j; //终点
}
}
begin = mst[minIndex]; //起点
end = minIndex; //终点
printf("%c-->%c : %d\n", getValue(begin), getValue(end), min);
lowCost[minIndex] = 0; //赋为0并入mst集合
int cost;
for(j = 0; j < n; j++){ //每次都重新更改lowCost和mst数组;
cost = edge[minIndex][j];
if(cost < lowCost[j]){
lowCost[j] = cost;
mst[j] = minIndex;
}
}
}
}3、完整代码、测试代码、测试结果
(1)、完整代码
#ifndef _GRAPH_H_
#define _GRAPH_H_
#include<iostream>
#include<queue>
using namespace std;
#define VERTEX_DEFAULT_SIZE 10
#define MAX_COST 0x7FFFFFFF
template<typename Type, typename E>
class Graph{
public:
bool isEmpty()const{
return curVertices == 0;
}
bool isFull()const{
if(curVertices >= maxVertices || curEdges >= curVertices*(curVertices-1)/2)
return true; //图满有2种情况:(1)、当前顶点数超过了最大顶点数,存放顶点的空间已满
return false; //(2)、当前顶点数并没有满,但是当前顶点所能达到的边数已满
}
int getCurVertex()const{
return curVertices;
}
int getCurEdge()const{
return curEdges;
}
public:
virtual bool insertVertex(const Type &v) = 0; //插入顶点
virtual bool insertEdge(const Type &v1, const Type &v2, E cost) = 0; //插入边
virtual bool removeVertex(const Type &v) = 0; //删除顶点
virtual bool removeEdge(const Type &v1, const Type &v2) = 0; //删除边
virtual int getFirstNeighbor(const Type &v) = 0; //得到第一个相邻顶点
virtual int getNextNeighbor(const Type &v, const Type &w) = 0; //得到下一个相邻顶点
public:
virtual int getVertexIndex(const Type &v)const = 0; //得到顶点下标
virtual void showGraph()const = 0; //显示图
virtual Type getValue(int index)const = 0;
public:
virtual void DFS(const Type &v) = 0;
virtual void BFS(const Type &v) = 0;
protected:
int maxVertices; //最大顶点数
int curVertices; //当前顶点数
int curEdges; //当前边数
};
template<typename Type, typename E>
class GraphMtx : public Graph<Type, E>{ //邻接矩阵继承父类矩阵
#define maxVertices Graph<Type, E>::maxVertices //因为是模板,所以用父类的数据或方法都得加上作用域限定符
#define curVertices Graph<Type, E>::curVertices
#define curEdges Graph<Type, E>::curEdges
public:
GraphMtx(int vertexSize = VERTEX_DEFAULT_SIZE){ //初始化邻接矩阵
maxVertices = vertexSize > VERTEX_DEFAULT_SIZE ? vertexSize : VERTEX_DEFAULT_SIZE;
vertexList = new Type[maxVertices]; //申请顶点空间
for(int i = 0; i < maxVertices; i++){ //都初始化为0
vertexList[i] = 0;
}
edge = new int*[maxVertices]; //申请边的行
for(i = 0; i < maxVertices; i++){ //申请列空间
edge[i] = new int[maxVertices];
}
for(i = 0; i < maxVertices; i++){ //赋初值为0
for(int j = 0; j < maxVertices; j++){
if(i != j){
edge[i][j] = MAX_COST; //初始化时都赋为到其它边要花的代价为无穷大。
}else{
edge[i][j] = 0; //初始化时自己到自己认为花费为0
}
}
}
curVertices = curEdges = 0; //当前顶点和当前边数
}
GraphMtx(Type (*mt)[4], int sz){ //通过已有矩阵的初始化
int e = 0; //统计边数
maxVertices = sz > VERTEX_DEFAULT_SIZE ? sz : VERTEX_DEFAULT_SIZE;
vertexList = new Type[maxVertices]; //申请顶点空间
for(int i = 0; i < maxVertices; i++){ //都初始化为0
vertexList[i] = 0;
}
edge = new int*[maxVertices]; //申请边的行
for(i = 0; i < maxVertices; i++){ //申请列空间
edge[i] = new Type[maxVertices];
}
for(i = 0; i < maxVertices; i++){ //赋初值为矩阵当中的值
for(int j = 0; j < maxVertices; j++){
edge[i][j] = mt[i][j];
if(edge[i][j] != 0){
e++; //统计列的边数
}
}
}
curVertices = sz;
curEdges = e/2;
}
~GraphMtx(){}
public:
bool insertVertex(const Type &v){
if(curVertices >= maxVertices){
return false;
}
vertexList[curVertices++] = v;
return true;
}
bool insertEdge(const Type &v1, const Type &v2, E cost){
int maxEdges = curVertices*(curVertices-1)/2;
if(curEdges >= maxEdges){
return false;
}
int v = getVertexIndex(v1);
int w = getVertexIndex(v2);
if(v==-1 || w==-1){
cout<<"edge no exit"<<endl; //要插入的顶点不存在,无法插入
return false;
}
if(edge[v][w] != MAX_COST){ //当前边已经存在,不能进行插入
return false;
}
edge[v][w] = edge[w][v] = cost; //因为是无向图,对称, 权值赋为cost;
return true;
} //删除顶点的高效方法
bool removeVertex(const Type &v){
int i = getVertexIndex(v);
if(i == -1){
return false;
}
vertexList[i] = vertexList[curVertices-1];
int edgeCount = 0;
for(int k = 0; k < curVertices; k++){
if(edge[i][k] != 0){ //统计删除那行的边数
edgeCount++;
}
}
//删除行
for(int j = 0; j < curVertices; j++){
edge[i][j] = edge[curVertices-1][j];
}
//删除列
for(j = 0; j < curVertices; j++){
edge[j][i] = edge[j][curVertices-1];
}
curVertices--;
curEdges -= edgeCount;
return true;
}
/* //删除顶点用的是数组一个一个移动的方法,效率太低。
bool removeVertex(const Type &v){
int i = getVertexIndex(v);
if(i == -1){
return false;
}
for(int k = i; k < curVertices-1; ++k){
vertexList[k] = vertexList[k+1];
}
int edgeCount = 0;
for(int j = 0; j < curVertices; ++j){
if(edge[i][j] != 0)
edgeCount++;
}
for(int k = i; k < curVertices-1; ++k)
{
for(int j = 0; j < curVertices; ++j)
{
edge[k][j] = edge[k+1][j];
}
}
for(int k = i; k < curVertices-1; ++k)
{
for(int j = 0; j < curVertices; ++j)
{
edge[j][k] = edge[j][k+1];
}
}
curVertices--;
curEdges -= edgeCount;
return true;
}
*/
bool removeEdge(const Type &v1, const Type &v2){
int v = getVertexIndex(v1);
int w = getVertexIndex(v2);
if(v==-1 || w==-1){ //判断要删除的边是否在当前顶点内
return false; //顶点不存在
}
if(edge[v][w] == 0){ //这个边根本不存在,没有必要删
return false;
}
edge[v][w] = edge[w][v] = 0; //删除这个边赋值为0,代表不存在;
curEdges--;
return true;
}
int getFirstNeighbor(const Type &v){
int i = getVertexIndex(v);
if(i == -1){
return -1;
}
for(int col = 0; col < curVertices; col++){
if(edge[i][col] != 0){
return col;
}
}
return -1;
}
int getNextNeighbor(const Type &v, const Type &w){
int i = getVertexIndex(v);
int j = getVertexIndex(w);
if(i==-1 || j==-1){
return -1;
}
for(int col = j+1; col < curVertices; col++){
if(edge[i][col] != 0){
return col;
}
}
return -1;
}
public:
void showGraph()const{
if(curVertices == 0){
cout<<"Nul Graph"<<endl;
return;
}
for(int i = 0; i < curVertices; i++){
cout<<vertexList[i]<<" ";
}
cout<<endl;
for(i = 0; i < curVertices; i++){
for(int j = 0; j < curVertices; j++){
if(edge[i][j] != MAX_COST){
cout<<edge[i][j]<<" ";
}else{
cout<<"@ ";
}
}
cout<<vertexList[i]<<endl;
}
}
int getVertexIndex(const Type &v)const{
for(int i = 0; i < curVertices; i++){
if(vertexList[i] == v){
return i;
}
}
return -1;
}
public:
Type getValue(int index)const{
return vertexList[index];
}
void DFS(const Type &v){
int n = Graph<Type, E>::getCurVertex();
bool *visit = new bool[n];
for(int i = 0; i < n; i++){
visit[i] = false;
}
DFS(v, visit);
delete []visit;
}
void BFS(const Type &v){
int n = Graph<Type, E>::getCurVertex();
bool *visit = new bool[n];
for(int i = 0; i < n; i++){
visit[i] = false;
}
cout<<v<<"-->";
int index = getVertexIndex(v);
visit[index] = true;
queue<int> q; //队列中存放的是顶点下标;
q.push(index);
int w;
while(!q.empty()){
index = q.front();
q.pop();
w = getFirstNeighbor(getValue(index));
while(w != -1){
if(!visit[w]){
cout<<getValue(w)<<"-->";
visit[w] = true;
q.push(w);
}
w = getNextNeighbor(getValue(index), getValue(w));
}
}
delete []visit;
}
public:
void MinSpanTree_Kruskal();
void MinSpanTree_Prim(const Type &v);
protected:
void DFS(const Type &v, bool *visit){
cout<<v<<"-->";
int index = getVertexIndex(v);
visit[index] = true;
int w = getFirstNeighbor(v);
while(w != -1){
if(!visit[w]){
DFS(getValue(w), visit);
}
w = getNextNeighbor(v, getValue(w));
}
}
private:
Type *vertexList; //存放顶点的数组
int **edge; //存放边关系的矩阵
};
//////////////////////////////////////////////////////////////////////////////////////////////////////
typedef struct MstEdge{
int x; //row
int y; //col
int cost;
}MstEdge;
int cmp(const void *a, const void *b){
return (*(MstEdge*)a).cost - (*(MstEdge*)b).cost;
}
bool isSame(int *father, int i, int j){
while(father[i] != i){
i = father[i];
}
while(father[j] != j){
j = father[j];
}
return i == j;
}
void markSame(int *father, int i, int j){
while(father[i] != i){
i = father[i];
}
while(father[j] != j){
j = father[j];
}
father[j] = i;
}
template<typename Type, typename E>
void GraphMtx<Type, E>::MinSpanTree_Kruskal(){
int n = Graph<Type, E>::getCurVertex(); //由于要用到父类的保护数据或方法,有模板的存在,必须加上作用域限定符;
MstEdge *edge1 = new MstEdge[n*(n-1)/2];
int k = 0;
for(int i = 0; i < n; i++){
for(int j = i+1; j < n; j++){
if(edge[i][j] != MAX_COST){
edge1[k].x = i;
edge1[k].y = j;
edge1[k].cost = edge[i][j];
k++;
}
}
}
qsort(edge1, k, sizeof(MstEdge), cmp);
int *father = new int[n];
Type v1, v2;
for(i = 0; i < n; i++){
father[i] = i;
}
for(i = 0; i < n; i++){
if(!isSame(father, edge1[i].x, edge1[i].y)){
v1 = getValue(edge1[i].x);
v2 = getValue(edge1[i].y);
printf("%c-->%c : %d\n", v1, v2, edge1[i].cost);
markSame(father, edge1[i].x, edge1[i].y);
}
}
}
template<typename Type, typename E>
void GraphMtx<Type, E>::MinSpanTree_Prim(const Type &v){
int n = Graph<Type, E>::getCurVertex();
int *lowCost = new int[n];
int *mst = new int[n];
int k = getVertexIndex(v);
for(int i = 0; i < n; i++){
if(i != k){
lowCost[i] = edge[k][i];
mst[i] = k;
}else{
lowCost[i] = 0;
}
}
int min;
int minIndex;
int begin;
int end;
for(i = 0; i < n-1; i++){
min = MAX_COST;
minIndex = -1;
for(int j = 0; j < n; j++){
if(lowCost[j] != 0 && lowCost[j] < min){
min = lowCost[j];
minIndex = j;
}
}
begin = mst[minIndex];
end = minIndex;
printf("%c-->%c : %d\n", getValue(begin), getValue(end), min);
lowCost[minIndex] = 0;
int cost;
for(j = 0; j < n; j++){
cost = edge[minIndex][j];
if(cost < lowCost[j]){
lowCost[j] = cost;
mst[j] = minIndex;
}
}
}
}
#endif(2)、测试代码
#include"Graph2.h"
int main(void){
GraphMtx<char,int> gm;
gm.insertVertex('A'); //0
gm.insertVertex('B'); //1
gm.insertVertex('C'); //2
gm.insertVertex('D'); //3
gm.insertVertex('E'); //4
gm.insertVertex('F'); //5
gm.insertEdge('A','B',6);
gm.insertEdge('A','C',1);
gm.insertEdge('A','D',5);
gm.insertEdge('B','C',5);
gm.insertEdge('B','E',3);
gm.insertEdge('C','E',6);
gm.insertEdge('C','D',5);
gm.insertEdge('C','F',4);
gm.insertEdge('D','F',2);
gm.insertEdge('E','F',6);
gm.showGraph();
gm.MinSpanTree_Kruskal();
cout<<"---------------------------------------------------------"<<endl;
gm.MinSpanTree_Prim('A');
return 0;
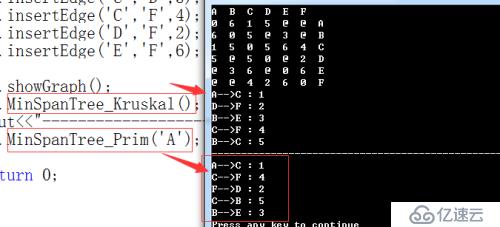
}(3)、测试结果
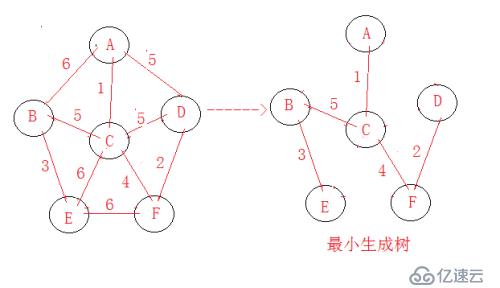
测试图模型:
免责声明:本站发布的内容(图片、视频和文字)以原创、转载和分享为主,文章观点不代表本网站立场,如果涉及侵权请联系站长邮箱:is@yisu.com进行举报,并提供相关证据,一经查实,将立刻删除涉嫌侵权内容。