对称矩阵和稀疏矩阵

对称矩阵

Matrix.h

#pragma once
 
template<class T>
class SymmetricMatrix
{
public:
 SymmetricMatrix(const T* a, size_t N) //对称矩阵 只存下三角
:_a(new T[N*(N + 1) / 2])
,_n(N)
{
size_t index = 0;
for (size_t i = 0; i < N; ++i)
{
for (size_t j = 0; j < N; ++j)
{
if (i >= j)
{
_a[index++] = a[i*N + j];
}
else
{
break;
}
}
}
}
 ~SymmetricMatrix()
 {
 }
void Display()
{
for (size_t i = 0; i < _n; ++i)
{
for (size_t j = 0; j <_n; ++j)
{
if (i >= j)//访问下三角
{
cout << _a[i*(i + 1) / 2 + j] << " ";
}
else  //访问上三角
{
cout << _a[j*(j + 1) / 2 + i] << " ";
}
}
cout << endl;
}
cout << endl;
}
T& Access(size_t i, size_t j)//访问i,j这里的数据
{
if (i < j)//若为上三角，交换
{
swap(i, j);
}
return _a[i(i + 1) / 2 + j];
}
protected:
T* _a;
size_t _n;
};
void Test1()
{
int a[5][5] =
{
{ 0, 1, 2, 3, 4 },
{ 1, 0, 1, 2, 3 },
{ 2, 1, 0, 1, 2 },
{ 3, 2, 1, 0, 1 },
{ 4, 3, 2, 1, 0 },
};
SymmetricMatrix<int> sm((int*)a, 5);
sm.Display();
}
 
Test.cpp
 
#include<iostream>
using namespace std;
#include"Matrix.h"
int main()
{
Test1();
system("pause");
return 0;
}

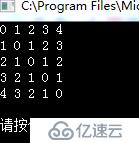
稀疏矩阵

Matrix.h

#include<vector>
template<class T>
struct Triple  //三元组
{
size_t _row;
size_t _col;
T _value;
 
Triple(size_t row=0, size_t col=0, const T& value=T())
:_row(row)
,_col(col)
, _value(value)
 
{}
};
 
template<class T>
class SqarseMatrix  //稀疏矩阵
{
public:
SqarseMatrix(size_t M, size_t N, const T& invalid)
:_M(M)
, _N(N)
, _invalid(invalid)
{}
SqarseMatrix(const T* a, size_t M, size_t N,const T& invalid)
:_M(M)
, _N(N)
, _invalid(invalid)
{
for (size_t i = 0; i < M; ++i)
{
for (size_t j = 0; j < N; ++j)
{
if (a[i*N + j] != invalid)
{
Triple<T> t(i, j, a[i*N + j]);
_a.push_back(t);
}
}
}
}
void Display()
{
size_t index = 0;
for (size_t i = 0; i < _M; ++i)
{
for (size_t j = 0; j <_N; ++j)
{
if (index<_a.size()&&i == _a[index]._row && j == _a[index]._col)//不能超出有效值的范围
{
cout << _a[index]._value << " ";
++index;
}
else //不是有效值则输出非法值
{
cout << _invalid << " ";
}
}
cout << endl;
}
cout << endl;
}
SqarseMatrix<T> Transport()  //转置
{
//o(有效数据的个数*列数)
SqarseMatrix<T> sm(_N,_M,_invalid);
 
for (size_t i = 0; i < _N; ++i)
{
size_t index = 0;
while (index < _a.size())
{
if (_a[index]._col == i)
{
Triple<T> t(_a[index]._col, _a[index]._row, _a[index]._value);
sm._a.push_back(t);
}
++index;
}
}
return sm;
}
 
SqarseMatrix<T> FastTransport()  //快速转置
{
//O(2*有效数据个数+列数)
SqarseMatrix<T> sm(_N, _M, _invalid);
int* rowCounts = new int[_N];
memset(rowCounts, 0, sizeof(int)*_N);//初始化
 
size_t index = 0;
while (index < _a.size())
{
rowCounts[_a[index]._col]++;
++index;
}
int* rowStart = new int[_N];
rowStart[0] = 0;
for (size_t i = 1; i < _N; ++i)
{
rowStart[i] = rowStart[i - 1] + rowCounts[i - 1];
}
index = 0;
sm._a.resize(_a.size());
while (index < _a.size())
{
size_t row = _a[index]._col;//转置前的列就是转置后的行
int& start = rowStart[row];//每行的起始位置，第一个起始位置就是0
Triple<T> t(_a[index]._col, _a[index]._row, _a[index]._value);
sm._a[start] = t;
++start;
 
++index;
}
delete[] rowCounts;
delete[] rowStart;
return sm;
}
protected:
vector<Triple<T>> _a;
size_t _M;
size_t _N;
T _invalid;
};
 
void Test2()
{
int a[6][5] = { { 1, 0, 3, 0, 5 },
                { 0, 0, 0, 0, 0 },
                { 0, 0, 0, 0, 0 },
                { 2, 0, 4, 0, 6 },
                { 0, 0, 0, 0, 0 }};
SqarseMatrix<int> sm((int*)a, 6, 5, 0);
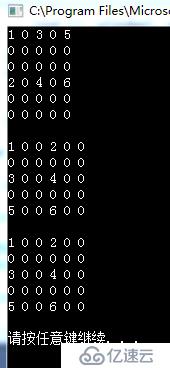
sm.Display();
SqarseMatrix<int> sm2 = sm.Transport();
sm2.Display();
SqarseMatrix<int> sm3 = sm.FastTransport();
sm3.Display();
}
 
Test.cpp
#include<iostream>
using namespace std;
#include"Matrix.h"
int main()
{
//Test1();
Test2();
system("pause");
return 0;
}