OpenCV中几何形状识别与测量

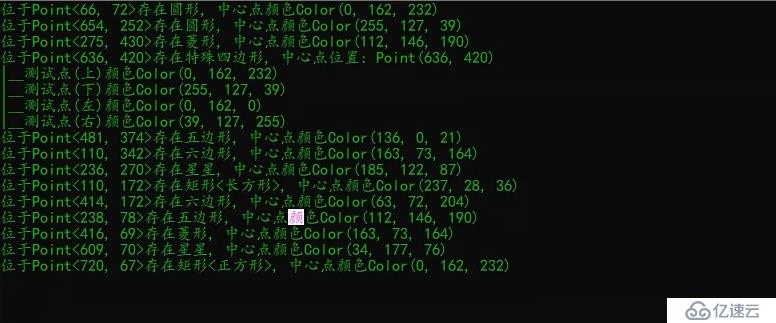
最近使用OpenCV3.3.0构建了一个识别图形的C/C++项目，可以识别的图形如下：三角形、正方形、长方形、菱形、圆形、五边形、六边形、五角星以及由不同颜色的两个三角形构成的特殊矩形。

中值滤波

中值滤波法是一种非线性平滑技术，它将每一像素点的灰度值设置为该点某邻域窗口内的所有像素点灰度值的中值.

中值滤波是基于排序统计理论的一种能有效抑制噪声的非线性信号处理技术，中值滤波的基本原理是把数字图像或数字序列中一点的值用该点的一个邻域中各点值的中值代替，让周围的像素值接近的真实值，从而消除孤立的噪声点。方法是用某种结构的二维滑动模板，将板内像素按照像素值的大小进行排序，生成单调上升（或下降）的为二维数据序列。二维中值滤波输出为g（x,y）=med{f(x-k,y-l),(k,l∈W)} ，其中，f(x,y)，g(x,y)分别为原始图像和处理后图像。W为二维模板，通常为3*3，5*5区域，也可以是不同的的形状，如线状，圆形，十字形，圆环形等。

中值滤波对脉冲噪声有良好的滤除作用，特别是在滤除噪声的同时，能够保护信号的边缘，使之不被模糊。这些优良特性是线性滤波方法所不具有的。此外，中值滤波的算法比较简单，也易于用硬件实现。所以，中值滤波方法一经提出后，便在数字信号处理领得到重要的应用。

Canny边缘检测

Canny边缘检测于1986年由JOHN CANNY首次在论文《A Computational Approach to Edge Detection》中提出，就此拉开了Canny边缘检测算法的序幕。Canny边缘检测是从不同视觉对象中提取有用的结构信息并大大减少要处理的数据量的一种技术，目前已广泛应用于各种计算机视觉系统。

Canny边缘检测算法可以分为以下五个步骤：
（一）使用高斯滤波器，以平滑图像，滤除噪声
为了尽可能减少噪声对边缘检测结果的影响，所以必须滤除噪声以防止由噪声引起的错误检测。为了平滑图像，使用高斯滤波器与图像进行卷积，该步骤将平滑图像，以减少边缘检测器上明显的噪声影响。大小为(2k+1)x(2k+1)的高斯滤波器核的生成方程式由下式给出：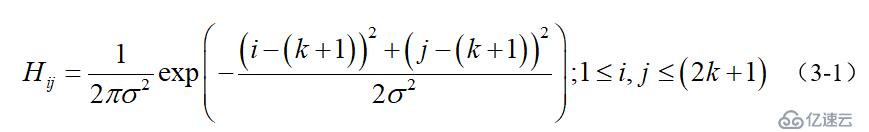

下面是一个sigma = 1.4，尺寸为3*3的高斯卷积核的例子（需要注意归一化）：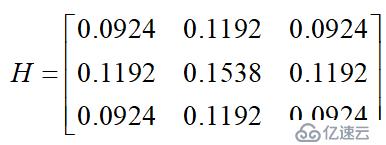

若图像中一个3*3的窗口为A，要滤波的像素点为e，则经过高斯滤波之后，像素点e的亮度值为：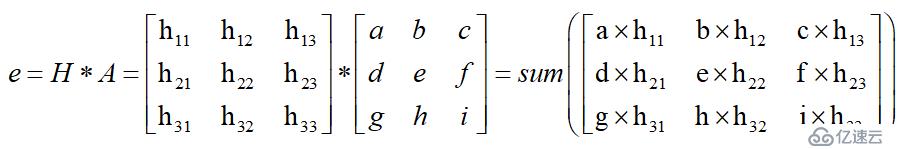

其中*为卷积符号，sum表示矩阵中所有元素相加求和。重要的是需要理解，高斯卷积核大小的选择将影响Canny检测器的性能。尺寸越大，检测器对噪声的敏感度越低，但是边缘检测的定位误差也将略有增加。一般5*5是一个比较不错的trade off。

（二）计算图像中每个像素点的梯度强度和方向
图像中的边缘可以指向各个方向，因此Canny算法使用四个算子来检测图像中的水平、垂直和对角边缘。边缘检测的算子（如Roberts，Prewitt，Sobel等）返回水平Gx和垂直Gy方向的一阶导数值，由此便可以确定像素点的梯度G和方向theta 。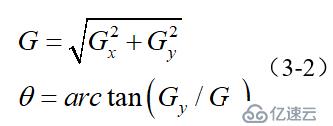

其中G为梯度强度， theta表示梯度方向，arctan为反正切函数。下面以Sobel算子为例讲述如何计算梯度强度和方向。x和y方向的Sobel算子分别为：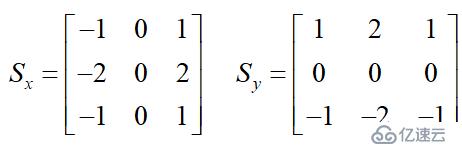

其中Sx表示x方向的Sobel算子，用于检测y方向的边缘； Sy表示y方向的Sobel算子，用于检测x方向的边缘（边缘方向和梯度方向垂直）。在直角坐标系中，Sobel算子的方向如下图所示：

若图像中一个3x3的窗口为A，要计算梯度的像素点为e，则和Sobel算子进行卷积之后，像素点e在x和y方向的梯度值分别为：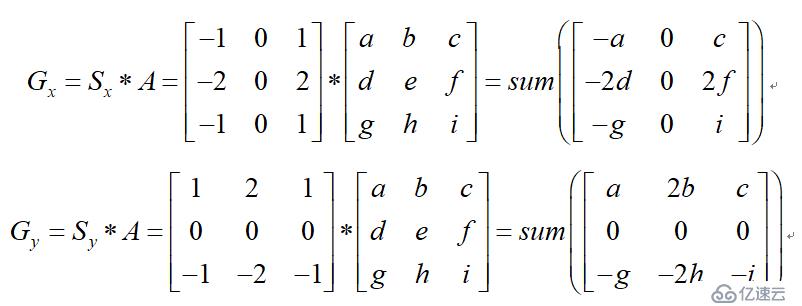

其中*为卷积符号，sum表示矩阵中所有元素相加求和。根据公式（3-2）便可以计算出像素点e的梯度和方向。
（三）应用非极大值（Non-Maximum Suppression）抑制，以消除边缘检测带来的杂散响应
非极大值抑制是一种边缘稀疏技术，非极大值抑制的作用在于“瘦”边。对图像进行梯度计算后，仅仅基于梯度值提取的边缘仍然很模糊。对于标准3，对边缘有且应当只有一个准确的响应。而非极大值抑制则可以帮助将局部最大值之外的所有梯度值抑制为0，对梯度图像中每个像素进行非极大值抑制的算法是：

1. 将当前像素的梯度强度与沿正负梯度方向上的两个像素进行比较。

2. 如果当前像素的梯度强度与另外两个像素相比最大，则该像素点保留为边缘点，否则该像素点将被抑制。

通常为了更加精确的计算，在跨越梯度方向的两个相邻像素之间使用线性插值来得到要比较的像素梯度，现举例如下：

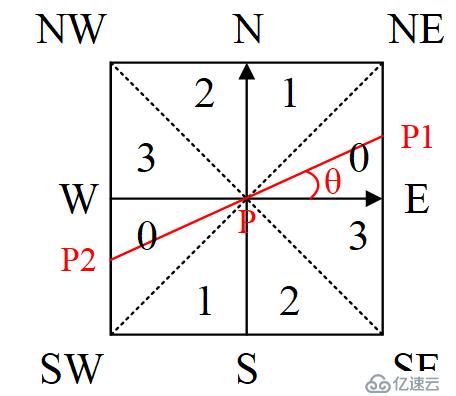
如图所示，将梯度分为8个方向，分别为E、NE、N、NW、W、SW、S、SE，其中0代表00~45o,1代表450~90o，2代表-900~-45o，3代表-450~0o。像素点P的梯度方向为theta，则像素点P1和P2的梯度线性插值为：

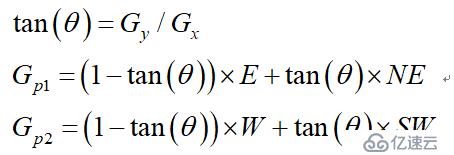
因此非极大值抑制的伪代码描写如下：

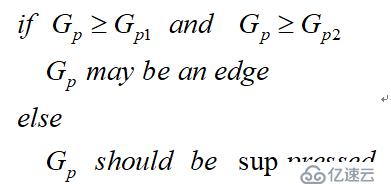
需要注意的是，如何标志方向并不重要，重要的是梯度方向的计算要和梯度算子的选取保持一致。

（四）应用双阈值（Double-Threshold）检测来确定真实的和潜在的边缘

在施加非极大值抑制之后，剩余的像素可以更准确地表示图像中的实际边缘。然而，仍然存在由于噪声和颜色变化引起的一些边缘像素。为了解决这些杂散响应，必须用弱梯度值过滤边缘像素，并保留具有高梯度值的边缘像素，可以通过选择高低阈值来实现。如果边缘像素的梯度值高于高阈值，则将其标记为强边缘像素；如果边缘像素的梯度值小于高阈值并且大于低阈值，则将其标记为弱边缘像素；如果边缘像素的梯度值小于低阈值，则会被抑制。阈值的选择取决于给定输入图像的内容。双阈值检测的伪代码描写如下：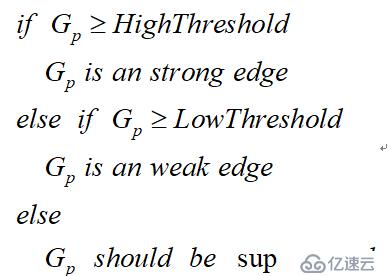

（五）通过抑制孤立的弱边缘最终完成边缘检测

到目前为止，被划分为强边缘的像素点已经被确定为边缘，因为它们是从图像中的真实边缘中提取出来的。然而，对于弱边缘像素，将会有一些争论，因为这些像素可以从真实边缘提取也可以是因噪声或颜色变化引起的。为了获得准确的结果，应该抑制由后者引起的弱边缘。通常，由真实边缘引起的弱边缘像素将连接到强边缘像素，而噪声响应未连接。为了跟踪边缘连接，通过查看弱边缘像素及其8个邻域像素，只要其中一个为强边缘像素，则该弱边缘点就可以保留为真实的边缘。抑制孤立边缘点的伪代码描述如下：

霍夫圆检测

Hough 变换的原理就是利用图像全局特征将边缘像素连接起来组成区域封闭边界，它将图像空间转换到参数空间，在参数空间对点进行描述，达到检测图像边缘的目的。该方法把所有可能落在边缘上的点进行统计计算，根据对数据的统计结果确定属于边缘的程度。Hough 变换的实质就是对图像进行坐标变换，把平面坐标变换为参数坐标，使变换的结果更易识别和检测。

已知圆的一般方程为：(x - a)^2 + (y - b)^2 = r^2，其中，(a, b)为圆心，r为圆的半径。

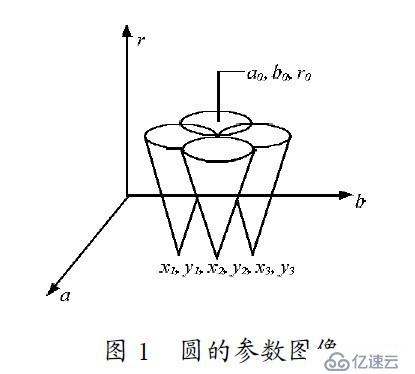
把X-Y平面上的圆转换到a-b-r参数空间，则图像空间中过(x, y)点圆对应参数空间中，高度r变化下的一个三维锥面，如下图：

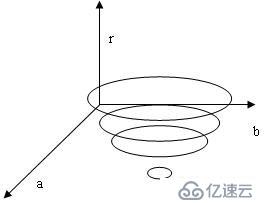
同理，过图像空间中任意一点的圆对应于参数空间中的一个三维锥面。因此，过图像空间上同一圆上的点，对应的参数空间中的三维锥面，在r高度必然相交于一点(a, b, r)。这样通过检测这一点可以得到圆的参数，相应的圆也可求得了。图像平面的方程转化为参数平面上的示意图如图所示：

霍夫直线检测

霍夫直线检测就比较简单了。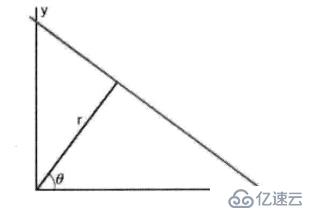

如上图所以，将一条直线由截距是表示为在极坐标系下：

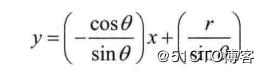
可以化简为：

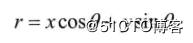
对于一个点（x0,y0）来说，可以通过这个点的一族直线统一定义为：

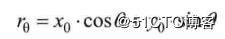
每一对(r0, theta)代表一条通过点（x0,y0）的直线。如果对于一个给定点（x0，y0），我们在极坐标对极径极角平面绘制出所有通过它的直线，将会得到一条正弦曲线。例如x0=8, y0=6的曲线如下所示：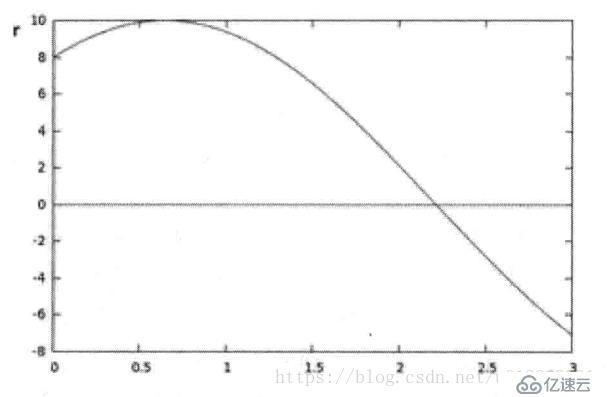

上图是r>0 theta(0,2*PI)。对图像中所有的点进行上述操作，如果两个点在一条直线上，那么两条正弦曲线将会交于一点：

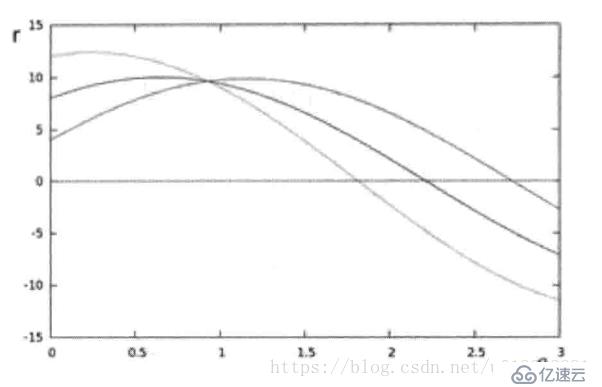
上图所有的三个点在一条直线上，一条直线能够通过在平面theta-r寻找交于一点的曲线数量来检测， 越多的 曲线交于一点就意味着这个交点表示的直线由更多的点组成，通过设置交于一点的曲线数的阈值来决定是否检测到一条直线。霍夫变换即追踪图像中每个点对应曲线间的交点，如果 交点数量超过了阈值，那么可以认为这个交点所代表的参数为原图像中的一条直线。

图像二值化

图像二值化（ Image Binarization）就是将图像上的像素点的灰度值设置为0或255，也就是将整个图像呈现出明显的黑白效果的过程。在数字图像处理中，二值图像占有非常重要的地位，图像的二值化使图像中数据量大为减少，从而能凸显出目标的轮廓。

将256个亮度等级的灰度图像通过适当的阈值选取而获得仍然可以反映图像整体和局部特征的二值化图像。在数字图像处理中，二值图像占有非常重要的地位，首先，图像的二值化有利于图像的进一步处理，使图像变得简单，而且数据量减小，能凸显出感兴趣的目标的轮廓。其次，要进行二值图像的处理与分析，首先要把灰度图像二值化，得到二值化图像。

轮廓发现

当我们通过阈值分割提取到图像中的目标物体后，我们就需要通过边缘检测来提取目标物体的轮廓，使用这两种方法基本能够确定物体的边缘或者前景。接下来，我们通常需要做的是拟合这些边缘的前景，如拟合出包含前景或者边缘像素点的最小外包矩形、圆、凸包等几何形状，为计算它们的面积或者模板匹配等操作打下坚实的基础。一个轮廓代表一系列的点（像素），这一系列的点构成一个有序的点集，所以可以把一个轮廓理解为一个有序的点集。 

在OpenCV中，提供了一个函数返回或者输出一个有序的点集或者有序的点集的集合（指多个有序的点集），函数findContour是从二值图像中来计算轮廓的，它可以使用Canny()函数处理的图像，因为这样的图像含有边缘像素；也可以使用threshold()或者adaptiveThreshold()处理后的图像，其边缘隐含在正负区域的交界处。

多边形拟合

主要功能是把一个连续光滑曲线折线化，对图像轮廓点进行多边形拟合。对比之前黑点连线，之后蓝色连线：

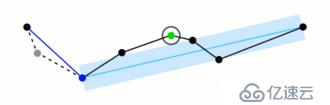
起始曲线是有序的一组点或线，距离维度ε> 0。该算法递归地划分线。 最初给出了第一点和最后一点之间的所有点。 它会自动标记要保存的第一个和最后一个点。 然后找到距离第一点和最后一点组成的线段的最远的点作为终点; 这一点在距离终点之间的近似线段的曲线上显然最远。 如果该点比线段更接近于ε，那么当前未被标记的任何点将被保存，而没有简化的曲线比ε更差的可以丢弃。如果离线段最远的点距离近似值大于ε，则必须保留该点。 该算法以第一个点和最远点递归地调用自身，然后以最远点和最后一个点（包括最远点被标记为保留）递归调用自身。当递归完成时，可以生成一个新的输出曲线，其中包括所有且仅标记为保留的点。

非参数Ramer-Douglas-Peucker ：ε 的选择通常是用户定义的。 像大多数线拟合/多边形近似/主点检测方法一样，通过使用由于数字化/量化的误差界限作为终止条件，可以使其非参数化，这种非参数RDP算法的MATLAB代码在这里可用。

识别结果

环境搭建讲解视频

https://gitee.com/bluemiaomiao/ImageFound/blob/master/video_x264.mp4

实现原理和项目代码

https://gitee.com/bluemiaomiao/ImageFound