您好,登录后才能下订单哦!
红黑树简介
红黑树是一种自平衡二叉查找树,也有着二叉搜索树的特性,保持着右边始终大于左边结点key的特性。前面提到过的AVL树,也是二叉搜索树的一种变形,红黑树没有达到AVL树的高度平衡,换句话说,它的高度,并没有AVL树那么高的要求,但他的应用却更加的广泛,实践中是相当高效的,他可以在O(log n)的时间内做查找、插入、删除操作。在C++ STL中,set、multiset、map、multimap等都应用到的红黑树的变体。
红黑树在平衡二叉搜索树的前提下,每个节点新增了 _color 这一成员变量,用来对各个节点做出标记。接下来,我们就来分析红黑树的插入算法。
一棵AVL树,需要满足以下几条要求。
1、每个结点,不是黑色就是红色
2、树的根结点必须是黑色
3、从根节点到叶子结点的任意一条路上,不允许存在两个连续的红色结点。
4、对于每个结点,从他开始到每个叶结点的简单路径上,黑色结点树相同。
这里多说一点,如果满足以上条件的话,从根节点开始,到叶子结点,最长的不会超过最长路径的两倍。(可以考虑最为极端的情况)
思路简析
和AVL树相同,要保证树的平衡性,必须要用到的是旋转算法。由于红黑树的情况比较多(尽管写起代码来不是很复杂),所以在这里旋转的过程中,我们不像AVL树一样,旋转的同时对平衡因子进行调整,红黑树的旋转算法,只是单纯调整当前结点与其parent 、grandparent 、uncle结点的相对位置,在旋转完成之后,我们再对结点颜色进行设置。
插入算法会在下面给出。
首先我们给出结点的定义。
enum Color
{
RED,
BLACK
};
template<typename K, typename V>
struct RBTreeNode
{
RBTreeNode<K, V>* _left;
RBTreeNode<K, V>* _right;
RBTreeNode<K, V>* _parent;
K _key;
V _value;
Color _color;
RBTreeNode(const K& key,const V& value)
:_left(NULL)
, _right(NULL)
, _parent(NULL)
, _key(key)
, _value(value)
, _color(RED)//默认构造红色结点
{}
};
_key为关键码(_key值是不允许重复的),_value为值,关于这里结点的构造函数,想多说一点,为什么结点颜色要默认给红色?很明显,一般情况下,黑色结点比红色结点多,但这里我们需要注意的是,我们针对的调整,其实大多数是红色。黑色结点下如果追加了红色结点,是不需要调整的,红色结点下如果多增加了一个黑色结点,是一定要进行调整的。
接下来开始插入结点。
1、处理特殊情况
当树为空树时,直接 new 一个结点给根,然后再改变颜色即可。
if (_root == NULL)
{
_root = new Node(key, value);
_root->_color = BLACK;
return true;
}2、树不为空树时,我们首先需要找到我们待插入结点的位置。由于红黑树是二叉搜索树,通过循环,比较待插入结点的key值和当前结点的大小,找到待插入结点的位置。同时给该节点开辟空间,确定和parent节点的指向关系。
Node* cur = _root;
Node* parent = NULL;
while (cur != NULL)
{
if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key, value);
if (key > (parent->_key))
{
parent->_right = cur;
cur->_parent = parent;
}
else
{
parent->_left = cur;
cur->_parent = parent;
} 当插入结点的parent结点为黑色结点时,不需要做任何调整,只需要和parent结点建立联系即可。
3、下面是需要我们特殊处理的几种情况。
我们给出四个Node结点 cur(待插入结点)、parent (cur的父亲结点)、grandparent(cur的祖父结点)、uncle(cur的叔叔结点)。
情况一、
parent为黑色,uncle存在且为红色
如图:
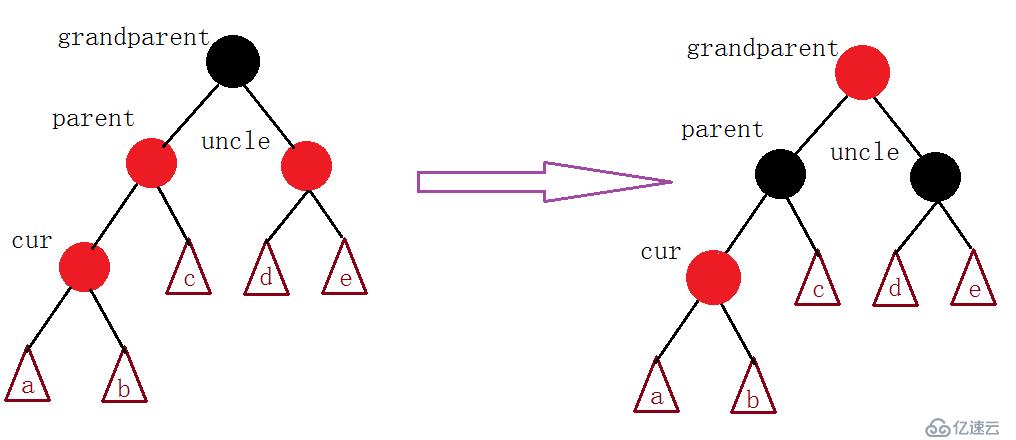
三角形结点只是表示可能存在的结点,可能为空。
当cur为新插入结点时,a-e结点均为空结点,由于不可以存在连续的红结点,因此,我们需要将parent结点和uncle结点变为黑色。细心的话可以发现,grandparent结点变为了红色,这是因为当grandparent不为根节点时,我们这棵子树的一条支路上的黑色结点就会多出一个,因此我们需要将grandparent结点变为红色,然后继续向上进行调整。在插入完成之后,我们只需要统一将根节点重新赋值为红色即可。
情况二、
parent为红色,uncle结点不存在,或uncle结点存在,但为黑色
如图:

看到第一张图的时候,不要怀疑这里画的有问题,这种情况是可能存在的,那就是说,cur是调整上来的,从我的上一种情况调整过来的,虽然看着grandparent的左右支路黑色结点数不相同,但我还有下面的三角形结点。
现在我这里就需要进行旋转,为什么这里不能直接颜色变换?因为我们抛过三角形结点,以grandparent结点为分界,最左支路和最后支路的,黑色结点数差一。旋转的图示如上图所示,以grandparent结点为轴,向右旋转。将grandparent结点作为parent结点的右子树进行旋转。同时需要的是,grandparent结点不一定是根节点,我们需要提前保留并判断grandparent->_parent结点,之后重新赋给parent->_parent。
情况三、
如果可以理解了第二种情况,第三种情况就容易理解了许多,和第二种情况一样,只不过cur是parent的右子树,我们需要先以parent为轴,向左旋转,得到上面这种情况之后,再以grandparent为轴向右旋转。如下图。

值得注意的一点,也是一开始写代码总是验证出错的一个问题,我们先以parent为轴左旋,之后看上图,cur此时变成了parent->_parent,如果此时按照情况二的处理方式,结点颜色一定会发生问题,因此,在上图中,我专门给出了一张图,将parent和cur指针交换,注意,只交换的是指针。
到这里,红黑树的基本情况以及处理完毕,再有的话就是当parent一开始就是在grandparent的右子树上的几种情况,和上面的旋转成镜像的关系。下面给出具体的代码:
bool Insert(const K& key,const V& value)
{
//空树
if (_root == NULL)
{
_root = new Node(key, value);
_root->_color = BLACK;
return true;
}
//构建节点,并插入到对应位置
Node* cur = _root;
Node* parent = NULL;
while (cur != NULL)
{
if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key, value);
if (key > (parent->_key))
{
parent->_right = cur;
cur->_parent = parent;
}
else
{
parent->_left = cur;
cur->_parent = parent;
}
//开始调整
while (cur != _root && parent->_color == RED)
{
//如果parent的color为RED,parent一定不是根节点,且祖父节点color为BLACK
Node* grandparentnode = parent->_parent;//grandparentnode->_color = BLACK;
if (parent == grandparentnode->_left)
{
Node* unclenode = grandparentnode->_right;//叔叔节点uncle
if (unclenode && (unclenode->_color == RED))//uncle不为空,且uncle->color为RED
{
parent->_color = BLACK;
unclenode->_color = BLACK;
grandparentnode->_color = RED;
cur = grandparentnode;
parent = cur->_parent;
}
else//uncle为空,或uncle->color为BLACK
{
if (cur == parent->_right)
{
RotateL(parent);
std::swap(parent, cur);
}
RotateR(grandparentnode);
parent->_color = BLACK;
grandparentnode->_color = RED;
break;
}
}
else//parent == grandparent->_right
{
Node* unclenode = grandparentnode->_left;
if (unclenode && (unclenode->_color == RED))//uncle存在,且color为 RED
{
parent->_color = BLACK;
unclenode->_color = BLACK;
grandparentnode->_color = RED;
cur = grandparentnode;
parent = cur->_parent;
}
else//uncle不存在,或uncle->color为黑色
{
if (cur == parent->_left)
{
RotateR(parent);
std::swap(cur,parent);
}
RotateL(grandparentnode);
grandparentnode->_color = RED;
parent->_color = BLACK;
break;
}
}
}
//统一将根节点的颜色变为黑色
_root->_color = BLACK;
return true;
}
红黑树结点的插入到这里就结束了,可以发现的是,我们其实一直在关注的是uncle结点,也就是cur的叔叔结点。这是红黑树插入思想里面的一个核心。
下面,就红黑树的基本特征,给出一段检验函数,判断红黑树是否满足要求。
bool IsBalance()
{
if (_root == NULL)
return true;
if (_root->_color == RED)
return false;
int count = 0;
Node* cur = _root;
while (cur != NULL)
{
if (cur->_color == BLACK)
{
count++;
}
cur = cur->_left;
}
int k = 0;
return _IsBalance(_root, count, k);
}
bool _IsBalance(Node* root, const int& count, int k)
{
if (root == NULL)
return true;
if (root != _root && root->_color == RED)
{
if (root->_parent->_color == RED)
{
cout << "连续红色结点" << root->_key << endl;
return false;
}
}
if (root->_color == BLACK)
k++;
if (root->_left == NULL && root->_right == NULL)
{
if (k == count)
return true;
else
{
cout << "黑色节点不相等" << root->_key << endl;
return false;
}
}
return _IsBalance(root->_left, count, k) \
&& _IsBalance(root->_right, count, k);
}
红黑树的应用远比AVL树多,还是一开始我们说的,其实红黑树的高度相对来说要比AVL树高出一些的,但这其实并不影响太多。因为我们的时间复杂度都是在O(log n)附近,当n = 10亿时,log(n)也仅仅只有30。但是另一方面,由于红黑树要比AVL树的要求低,所以当我们插入一个结点时,相对来说调整的次数也就少了许多,这个是红黑树的优势。
------muhuizz整理
免责声明:本站发布的内容(图片、视频和文字)以原创、转载和分享为主,文章观点不代表本网站立场,如果涉及侵权请联系站长邮箱:is@yisu.com进行举报,并提供相关证据,一经查实,将立刻删除涉嫌侵权内容。