您好,登录后才能下订单哦!

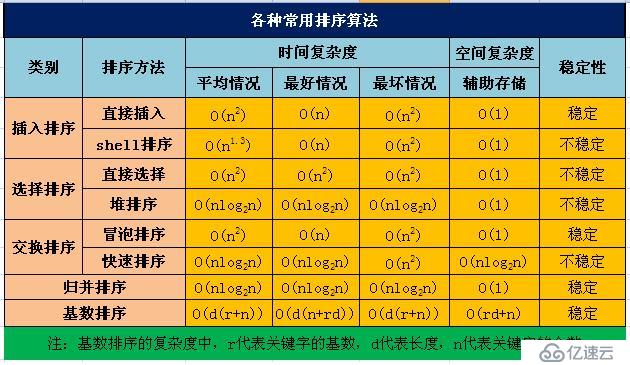
常见的交换排序算法有冒泡排序和快速排序
冒泡排序
冒泡排序算法的基本原理如下:(从后往前)
1. 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
2. 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。在这一点,最后
3. 的元素应该会是最大的数。
4. 针对所有的元素重复以上的步骤,除了最后一个。
5. 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
算法示意图如下:动画演示
经过优化过后的代码如下:
void BubbleSort(int* a, size_t n) //冒泡排序优化版
{
assert(a);
bool flag = true;
for (int i = 0; i < n - 1 && flag; ++i)
{
flag = false;
for (int j = 1; j < n - i; ++j)
{
if (a[j - 1] > a[j])
{
std::swap(a[j - 1], a[j]);
flag = true;
}
}
}
}性能分析

 若文件的初始状态是正序的,一趟扫描即可完成排序,所以,冒泡排序最好时间
若文件的初始状态是正序的,一趟扫描即可完成排序,所以,冒泡排序最好时间
复杂度为O(N)。
 若初始文件是反序的,需要进行 N -1 趟排序。每趟排序要进行 N - i 次关键字的
若初始文件是反序的,需要进行 N -1 趟排序。每趟排序要进行 N - i 次关键字的
比较(1 ≤ i ≤ N - 1)。在这种情况下,比较和移动次数均达到最大值,所以,冒泡排
序的最坏时间复杂度为O(N2)。
因此,冒泡排序的平均时间复杂度为O(N2)。
总结起来,其实就是一句话:当数据越接近正序时,冒泡排序性能越好。
稳定性
冒泡排序就是把小的元素往前调或者把大的元素往后调。比较是相邻的两个元素比
较,交换也发生在这两个元素之间。
所以相同元素的前后顺序并没有改变,所以冒泡排序是一种稳定排序算法。
快速排序
快速排序的基本原理:
1.通过一趟排序将要排序的数据分割成独立的两部分:分割点左边都是比它小
的数,右边都是比它大的数。
2. 然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归
进行,以此达到整个数据变成有序序列。
算法示意图如下:
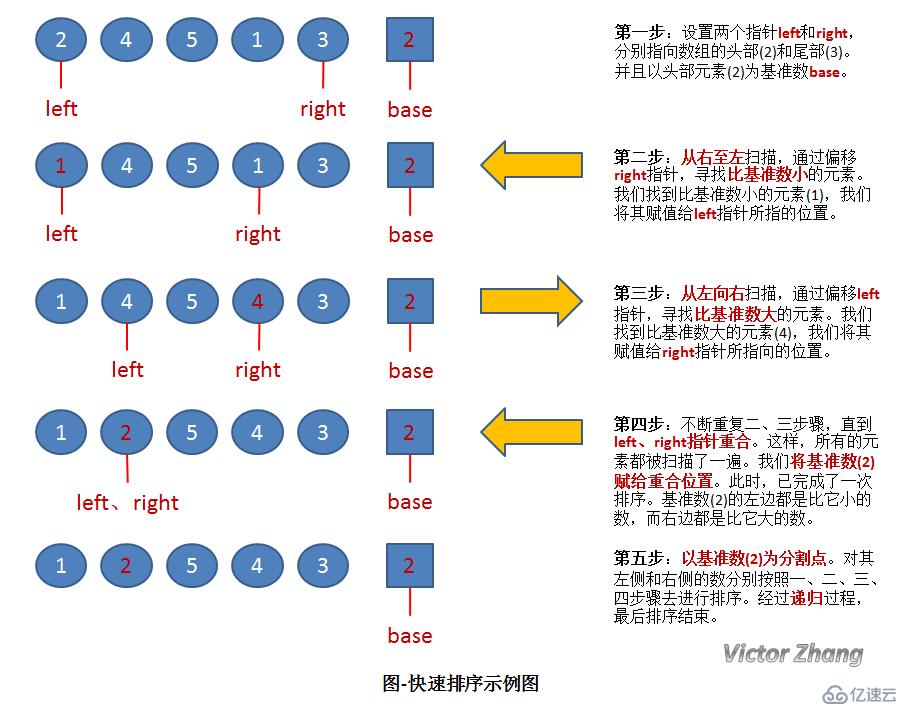
代码如下:
比较直观的代码:
int Partition(int* a, int left, int right)
{
assert(a);
int key = a[right];
int begin = left;
int end = right - 1;
while (begin < end)
{
while (begin < end && a[begin] <= key)
{
++begin;
}
while (begin < end && a[end] >= key)
{
--end;
}
std::swap(a[begin], a[end]);
}
if (a[begin] > key) // 大于key再交换
{
std::swap(a[begin], a[right]);
return begin;
}
else
{
return right;
}
}
void QuickSort(int* a, int left, int right)
{
assert(a);
if (left < right)
{
int pivotloc = Partition(a, left, right);
QuickSort(a, left, pivotloc-1);
QuickSort(a, pivotloc+1, right);
}
}比较简单的代码:(挖坑填数发)
int Partition(int* a, int left, int right)
{
assert(a);
int base = a[left];
while (left < right)
{
while (left < right && a[right] >= base) //注意这里一定要有等于
--right; //否则会有死循环
a[left] = a[right];
while (left < right && a[left] <= base)
++left;
a[right] = a[left];
}
a[left] = base;
return left;
}
void QuickSort(int* a, int left, int right)
{
assert(a);
if (left < right)
{
int pivotloc = Partition(a, left, right);
QuickSort(a, left, pivotloc-1);
QuickSort(a, pivotloc+1, right);
}
}非递归写法:
void QuickSortNoRe(int* a, int left, int right) //快排非递归
{
assert(a);
if (left >= right)
return;
stack<int> st;
st.push(right);
st.push(left);
while (!st.empty())
{
int _left = st.top();
st.pop();
int _right = st.top();
st.pop();
int mid = Partition(a, _left, _right);
if (_left < mid - 1)
{
st.push(mid - 1);
st.push(_left);
}
if (mid + 1 < _right)
{
st.push(_right);
st.push(mid + 1);
}
}
}性能分析
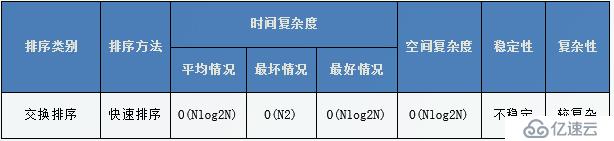
而当数据随机分布时,以第一个关键字为基准分为两个子序列,两个子序列的元素
个数接近相等,此时执行效率最好。
当每次递归的基准值都是当前区间中最大或者最小的数时,此时效率最差
稳定性
在快速排序中,相等元素可能会因为分区而交换顺序,所以它是不稳定的算法。
免责声明:本站发布的内容(图片、视频和文字)以原创、转载和分享为主,文章观点不代表本网站立场,如果涉及侵权请联系站长邮箱:is@yisu.com进行举报,并提供相关证据,一经查实,将立刻删除涉嫌侵权内容。